斜率优化学习笔记
斜率优化学习笔记
前置知识
理解本文可能需要的前置知识：动态规划、初中数学知识。
线性规划问题
线性规划问题是研究线性约束条件下线性目标函数极值问题的方法总称，是运筹学的一个分支，在多方面均有应用。
在本文我们主要讨论的线性规划问题是：用一个斜率为定值 \(k\) 的直线 \(l:y=kx+b\) 切一个点集 \(S\) 的凸包，要求 \(l\) 与凸包有交点，求最小（最大）的 \(y\) 轴上截距 \(b\)。下文均默认求最小截距，最大截距可以同理求得。
例如对点集 \(S=\{(2,3),(3,5),(3,2),(4,2.5),(5,4),(4,4),(4,6)\}\) 和斜率 \(k=3\) 的线性规划问题如下：
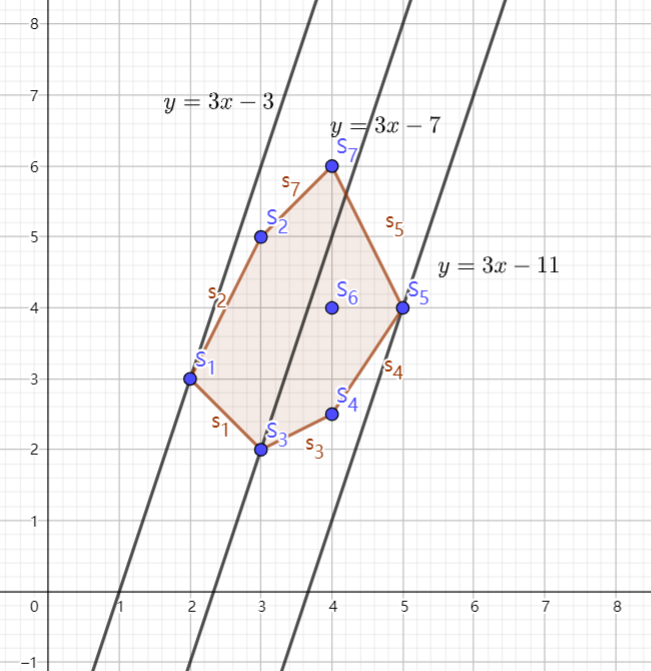
可以看出，最小的截距为 \(b=-11\)。
我们继续分析上面这张图，当 \(k > 0\) 时，究竟哪些点可能对答案有贡献呢？
发现是凸包的下凸壳（如图）：
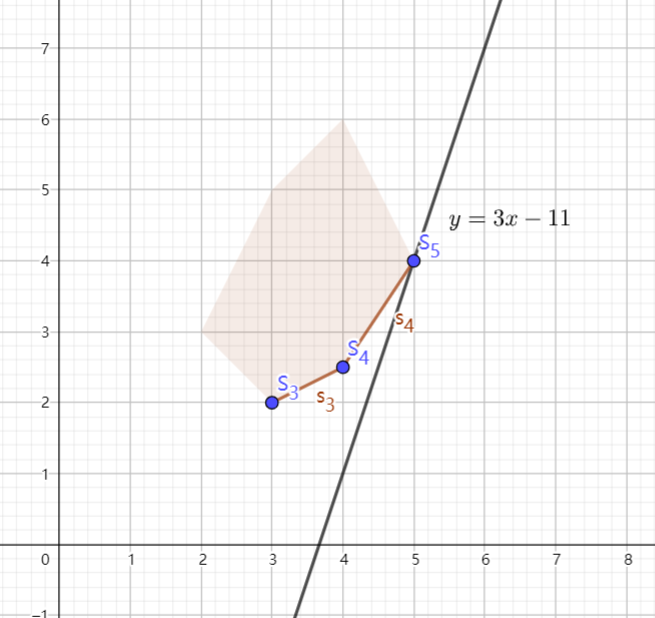
不管斜率为哪个正数，最小的截距一定在直线 \(l\) 过下凸壳上一个顶点的时候取到，例如上图就是过的 \(S_5(5,4)\)。
斜率优化用到的几种线性规划问题
斜率优化中，我们需要解决 \(n\) 个线性规划问题。在第 \(i\) 个线性规划问题中，我们的点集是 \(S=\{(x_1,y_1),(x_2,y_2),\cdots,(x_{i-1},y_{i-1})\}\)，同时有一个斜率 \(k_i\)。假设这个线性规划问题的答案（最小截距）为 \(b_i\)，则会向点集中添加一个新点 \((x_i,f(b_i))\)，其中 \(f\) 是一个 \(\R\to\R\) 函数，因题而异。
考虑以下问题：
（一）所有问题的 \(x\) 单调不降，\(k\) 单调不降。
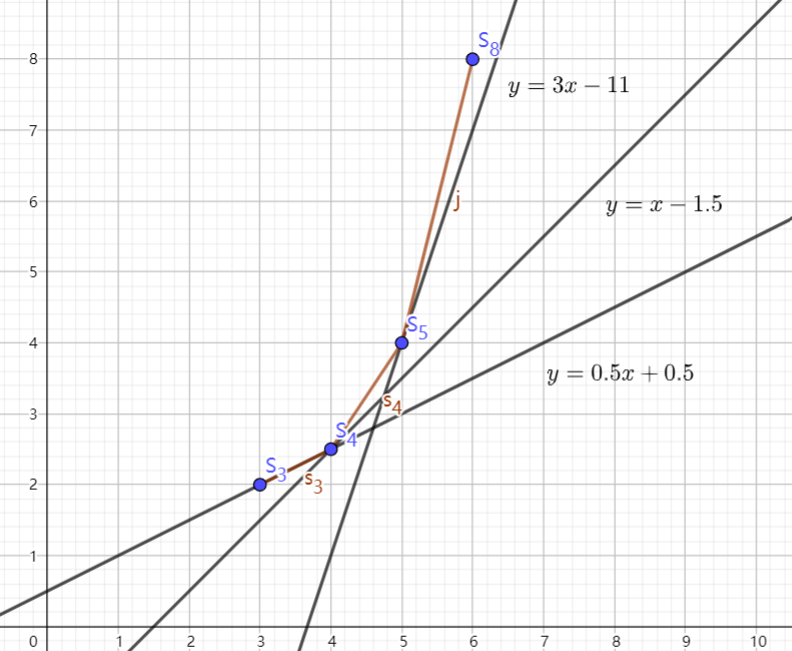
可以发现，因为 \(k\) 单调不降，所以每个问题的决策点一定是一直向右走的，我们可以使用单调队列维护下凸壳，查询时比较队首线段的斜率和 \(k\) 的大小关系，找到第一个斜率 \(\ge k\) 的线段的端点，计算截距即可。
加入点的时候，因为 \(x\) 单调不降，我们在队尾比较斜率，弹一些在当前点内侧（上方）的点，然后把当前点加进去即可。
时间复杂度 \(\mathcal{O}(n)\)。
（二）所有问题的 \(x\) 单调不降。
我们依然维护一个单调队列，只不过由于决策点不一定一直向右，我们不能队首出队，每次查询只能二分找决策点，加点方式不变。
时间复杂度 \(\mathcal{O}(n\log n)\)。
（三）无特殊性质。
这时候单调队列就不好使了，我们需要用平衡树维护下凸壳，然后找前驱后继。另一种解法是 CDQ 分治。
时间复杂度 \(\mathcal{O}(n\log n)\)。
斜率优化
我们以 [APIO2010]特别行动队 为例讲一下斜率优化。并不想举更经典的 任务安排 ，因为那题的 \(\mathcal{O}(n^2)\) 的转移方程并不是特别一眼。
我们记 \(s_i=\sum\limits_{j-1}^ix_j\)，\(f(x)=ax^2+bx+c\)。设 \({dp}_i\) 表示考虑前 \(i\) 个士兵，最大的修正战斗力为多少。不难推出 \({dp}_i=\max\limits_{0\le j < i}\{{dp}_j+f(s_i-s_j)\}\)（\(j\) 是上一个特别行动队的末尾，\(j+1\sim i\) 是当前特别行动队）。
假设 \(j\) 是 \({dp}_i\) 转移的决策点，则有 \({dp}_i={dp}_j+a(s_i-s_j)^2+b(s_i-s_j)+c\)，拆开就是 \({dp}_i={dp}_j+as_i^2-2as_is_j+as_j^2+bs_i-bs_j+c\)。
那这跟线性规划问题有啥关系呢？我们能不能从上面看出一个解析式出来？其中 \(j\) 是点集中点的编号，\(i\) 相关（除了 \({dp}_i\)）是已知量。
初学可能看不出来，这里有一个技巧：把只含 \(j\) 的项放到等号一边，作为纵坐标 \(y\)；把同时含 \(i,j\) 的交叉项放到另一边，\(i\) 部分和 \(j\) 部分分别作为斜率 \(k\) 和横坐标 \(x\)；只含 \(i\) 的项也放到这里，作为待求的截距 \(b\)。
例如上面式子可以写成 \(\color{red}{{dp}_j+as_j^2-bs_j}=\color{orange}{2as_i}\color{blue}{s_j}+\color{green}{{dp}_i-as_i^2-bs_i-c}\)，其中\(\color{red}{红色}\)、\(\color{orange}{橙色}\)、\(\color{blue}{蓝色}\)、\(\color{green}{绿色}\)分别对应了 \(y,k,x,b\)。
我们用单调队列维护凸壳（注意这里求 \(\max\) 所以要维护上凸壳），然后找到决策点后求出 \(dp\) 即可。
显然由于 \(x > 0\)，前缀和单调递增，\(k,x\) 单调递增。
//By: Luogu@rui_er(122461)
#include <bits/stdc++.h>
#define rep(x,y,z) for(ll x=y;x<=z;x++)
#define per(x,y,z) for(ll x=y;x>=z;x--)
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;
const ll N = 1e6+5;
ll n, s[N], a, b, c, dp[N], q[N], l = 1, r = 1;
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
ll x(ll i) {return s[i];}
ll y(ll i) {return dp[i] + a * s[i] * s[i] - b * s[i];}
ll k(ll i) {return 2 * a * s[i];}
double slope(ll i, ll j) {return 1.0 * (y(j) - y(i)) / (x(j) - x(i));}
/*
* y = k * x + b
* b = y - k * x
**/
int main() {
scanf("%lld%lld%lld%lld", &n, &a, &b, &c);
rep(i, 1, n) {
scanf("%lld", &s[i]);
s[i] += s[i-1];
}
rep(i, 1, n) {
while(l < r && slope(q[l], q[l+1]) > k(i)) ++l;
int j = q[l];
dp[i] = dp[j] + a * (s[i] - s[j]) * (s[i] - s[j]) + b * (s[i] - s[j]) + c;
while(l < r && slope(q[r-1], q[r]) <= slope(q[r], i)) --r;
q[++r] = i;
}
printf("%lld\n", dp[n]);
return 0;
}
