舞蹈链(DLX)学习笔记
舞蹈链(DLX)学习笔记
我好菜
WC 没听懂,于是来自己写一下。
前置知识:搜索,大致了解双向链表、循环链表。
精确覆盖问题
有一个 \(n\times m\) 的 \(0/1\) 矩阵,选出若干行,使得每一列恰有一个 \(1\)。
换句话说,有 \(n\) 个集合,集合元素取值在 \(1\sim m\),选出一些集合,使得它们的并是全集,且任意两个的交是空集。
容易想到的暴力
暴力一
枚举选哪些行,暴力 check。
时间复杂度为 \(\mathcal{O}(2^n\cdot nm)\)。
暴力二
记一下现在选的元素的并(状压后为或),可以降低复杂度。
时间复杂度为 \(\mathcal{O}(2^n\cdot n)\)。
X 算法
X 算法是 Donald E. Knuth 提出的一个算法。这个名字可能会很熟悉,因为他是 KMP 中的 K。
我们从 OI Wiki 贺一个矩阵过来,以这个为例:
首先尝试选取第一行,发现这一行有三个 \(1\),因为一列只能有一个 \(1\),所以它们所在列不能再有 \(1\) 了。
在下图中第一行被标为\(\color{blue}{蓝色}\),\(1\) 所在列被标为\(\color{red}{红色}\),在那些列中有 \(1\) 的行被标为\(\color{orange}{橙色}\)(记住这些颜色的意义,在后面不会再重复写了):
那么上图中的\(\color{orange}{橙色}\)的行都不能取了,因为会与取了的\(\color{blue}{蓝色}\)的行冲突。
\(\color{blue}{蓝色}\)的行取过了,\(\color{orange}{橙色}\)的行都不能取了,留着只会浪费资源,所以把它们删掉。\(\color{red}{红色}\)的列中所有的 \(1\) 所在行都被删掉了,只剩 \(0\) 了,没有意义,也删掉。
就得到了下面这个可爱的小矩阵(即没有染色的部分):
我们继续重复上面的步骤,选择第一行标成\(\color{blue}{蓝色}\),把所有的 \(1\) 所在列标成\(\color{red}{红色}\),在\(\color{red}{红色}\)列中找到所有的 \(1\) 把所在行标为\(\color{orange}{橙色}\):
\(\color{orange}{橙色}\)行会与\(\color{blue}{蓝色}\)行冲突,继续把标色的部分删掉:
发现矩阵空了!但是上一次选择的行:
不是全 \(1\) 的,这意味这一行中 \(0\) 所在列无法被任何行选择了,因此这个选择方案不合法。我们回溯到上一步:
这次选择第二行:
把它们删掉:
继续递归,选择第一行并完成标记:
把它们删掉:
发现矩阵又空了!这次说明了什么呢?上一个选择的行全为 \(1\),在小矩阵中所有列都覆盖了。而大矩阵中其他列呢?其他列在前面的步骤就被删掉了,说明它们已经被标成了\(\color{red}{红色}\),不然不会被删除。而\(\color{red}{红色}\)列的意义是(好像打脸了说好的“不会再重复写了”呢)选择的\(\color{blue}{蓝色}\)行中 \(1\) 所在列,说明这一列已经有 \(1\) 了。整个选择符合题意,找出了一种解,算法结束。
为了确保能够正确理解,下面会重新给你一遍这个矩阵,强烈建议不要看上面内容,手玩一遍再继续看!
总结一下 X 算法的流程:
- 对于现在的矩阵 \(M\),选出一行标成\(\color{blue}{蓝色}\),并相应地标记\(\color{red}{红色}\)和\(\color{orange}{橙色}\),将\(\color{blue}{蓝色}\)行放到答案 \(S\) 中。
- 删除所有被染色的行和列,把它们删除,得到可爱的小矩阵 \(M'\)。
- 如果 \(M'\) 为空,且刚刚选择的\(\color{blue}{蓝色}\)行全为 \(1\),找到了一种解,返回被删除的行组成的集合 \(S\)。
- 如果 \(M'\) 为空,但刚刚选择的\(\color{blue}{蓝色}\)行不全为 \(1\),则无解,返回无解并回溯。
- 如果 \(M'\) 不为空,回到第一步继续递归。
- 如果尝试了所有行都无解,返回无解并回溯。
DLX 算法
闲话
我们需要大量的“删除行”“删除列”“恢复行”“恢复列”操作,删除在递归时用,恢复在回溯时用。那么这东西怎么维护呢?Donald E. Knuth 想到了双向十字链表。
在双向十字链表上的操作被形象地比喻成“跳跃”,因此用双向十字链表优化的 X 算法被称为“Dancing Links X”(DLX/舞蹈链)。
宏定义
#define move(i,A,x) for(int i=A[x];i!=x;i=A[i])
也就是从 \(A_x\) 开始,向 \(A\) 方向走,直到走一圈。
这个链表是循环链表,\(A\) 为 \(L,R,U,D\),详见下面。
双向十字链表定义
一个双向十字链表的节点存储所在的行号和列号,同时指出去四个指针,如图:
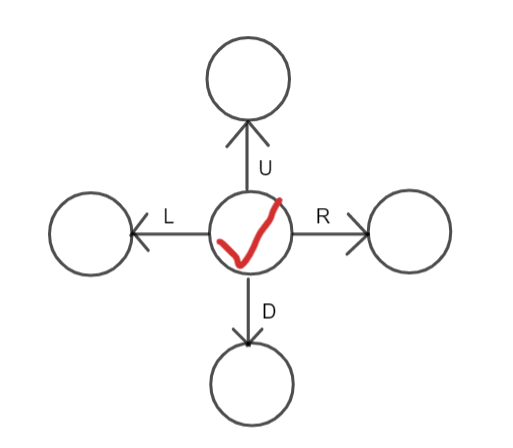
这个双向十字链表是循环链表,也就是说,每一行最左边节点的 \(L\) 指针指向最右边节点,其他三个指针同理。
每一行的行首有一个行指示(为下文的 \(hd\) 数组),每一列的列首有一个列指示(是一个节点,编号从 \(0\sim m\),\(i\) 号即为第 \(i\) 列的列首标记)。
我们还用 \(sz\) 表示每一列的元素个数。
在双向十字链表中,我们只维护为 \(1\) 的点,不维护为 \(0\) 的点。点的总数为 \(tot\)。
\(ans\) 类似于上文 X 算法中的 \(S\),\(totAns\) 是选出行的个数。
int n, m, hd[N], sz[N], L[N], R[N], U[N], D[N], col[N], row[N], tot, ans[N], totAns;
remove 操作
remove(c):在舞蹈链中删除第 \(c\) 列及其相关行。
我们知道第 \(c\) 列的列首标记为 \(c\),首先把 \(c\) 从横向链表中删除:
L[R[c]] = L[c];
R[L[c]] = R[c];
相当于这个操作:(第一行的节点是虚拟节点,为列指示标记)
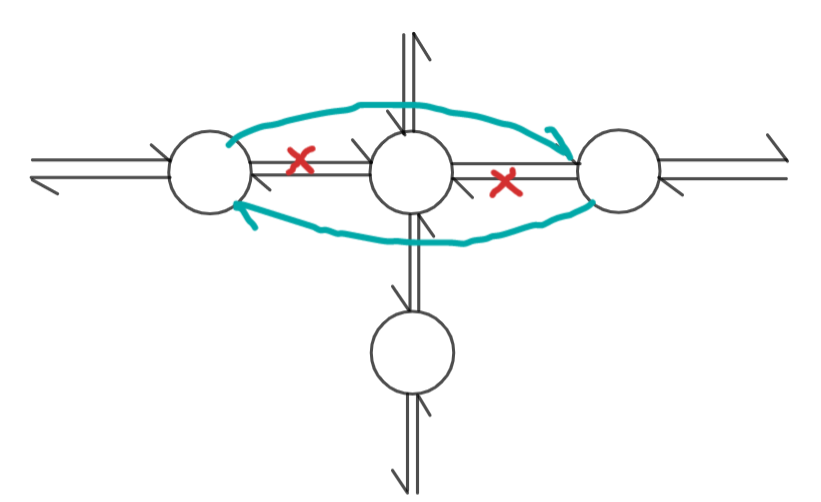
然后顺着这一列往下走,把每一行都删掉。类似上面的代码,只不过更改的是 \(U,D\) 指针。不要忘记修改每一列的节点数 \(sz\)。
void remove(int c) {
L[R[c]] = L[c];
R[L[c]] = R[c];
move(i, D, c) {
move(j, R, i) {
U[D[j]] = U[j];
D[U[j]] = D[j];
--sz[col[j]];
}
}
}
recover 操作
recover(c):在舞蹈链中还原第 \(c\) 列及其相关行。
就是 remove(c) 的逆操作,不详细讲解,注意要把 remove 的操作顺序反过来。
void recover(int c) {
move(i, U, c) {
move(j, L, i) {
U[D[j]] = j;
D[U[j]] = j;
++sz[col[j]];
}
}
L[R[c]] = c;
R[L[c]] = c;
}
build 操作
build(r,c):初始化一个 \(r\times c\) 的双向十字链表,初始为空(除了列指示标记)。
新建 \(c+1\) 个点作为列指示,编号为 \(0\sim c\),则 \(0\) 为列指示标记的行指示(有点绕),\(i\) 为第 \(i\) 列的列指示。
因为是循环链表,所以 \(i\) 的 \(L,R,U,D\) 标记分别为 \(i-1,i+1,i,i\)(取模意义下)。
void build(int r, int c) {
memset(hd, 0, sizeof(hd));
memset(sz, 0, sizeof(sz));
n = r; m = c; tot = c;
rep(i, 0, c) {
L[i] = !i ? c : i - 1;
R[i] = i == c ? 0 : i + 1;
U[i] = i;
D[i] = i;
}
}
insert 操作
insert(r,c):在位置 \((r,c)\) 插入一个节点。
分两类讨论:
如果第 \(r\) 行是空的,那么新建一个节点,并使 \(hd_r\) 指向这个节点。
如果第 \(r\) 行不是空的,那么用以下方式把节点插进去(假设这个节点编号为 \(u\)):
- 把 \(u\) 插到 \(c\) 的正下方,\(c\) 下面原来的节点放到 \(u\) 下面,参考图论中的链式前向星。
- 把 \(u\) 插到 \(hd_r\) 的正右方,\(hd_r\) 右面原来的节点放到 \(u\) 右面,参考图论中的链式前向星。
- 记得更新所在列的节点数 \(sz\)。
相当于这个操作:
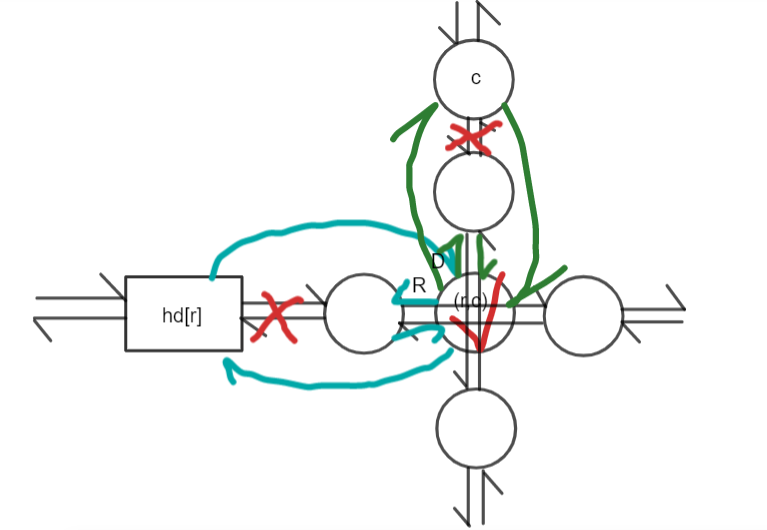
注意在青色边和绿色边上标的 \(R\) 和 \(D\) 可能不符合直觉,但确实是这样的,这保证了复杂度。
这一步比较难理解,建议仔细看看。
void insert(int r, int c) {
++tot; ++sz[c];
row[tot] = r; col[tot] = c;
U[tot] = c;
D[tot] = D[c];
U[D[c]] = tot;
D[c] = tot;
if(!hd[r]) {
hd[r] = tot;
L[tot] = tot;
R[tot] = tot;
}
else {
L[tot] = hd[r];
R[tot] = R[hd[r]];
L[R[hd[r]]] = tot;
R[hd[r]] = tot;
}
}
dance 操作
dance():递归地解决剩余的矩阵。
类似于前文 X 算法部分,这部分的操作如下:
- 如果 \(0\) 的 \(R\) 指针为空,则矩阵为空,记录答案并返回。
- 选择一列并删掉。
- 遍历这一列所有 \(1\),删掉对应行。
- 递归调用
dance(),返回是否有解,如果无解,恢复被删除的部分。 - 如果没有可行选法,则返回无解。
不过为了减小搜索树,在第二步时常使用启发式的优化,找到 \(sz\) 最小(\(1\) 最少)的列。
bool dance() {
int c = R[0];
if(!c) return 1;
move(i, R, 0) if(sz[i] < sz[c]) c = i;
remove(c);
++totAns;
move(i, D, c) {
ans[totAns] = row[i];
move(j, R, i) remove(col[j]);
if(dance()) return 1;
move(j, L, i) recover(col[j]);
}
recover(c);
--totAns;
return 0;
}
完整代码
//By: Luogu@rui_er(122461)
#include <bits/stdc++.h>
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;
const int N = 2e4+5;
int n, m, x;
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
struct DLX {
int n, m, hd[N], sz[N], L[N], R[N], U[N], D[N], col[N], row[N], tot, ans[N], totAns;
#define move(i,A,x) for(int i=A[x];i!=x;i=A[i])
void remove(int c) {
L[R[c]] = L[c];
R[L[c]] = R[c];
move(i, D, c) {
move(j, R, i) {
U[D[j]] = U[j];
D[U[j]] = D[j];
--sz[col[j]];
}
}
}
void recover(int c) {
move(i, U, c) {
move(j, L, i) {
U[D[j]] = j;
D[U[j]] = j;
++sz[col[j]];
}
}
L[R[c]] = c;
R[L[c]] = c;
}
void build(int r, int c) {
memset(hd, 0, sizeof(hd));
memset(sz, 0, sizeof(sz));
n = r; m = c; tot = c;
rep(i, 0, c) {
L[i] = !i ? c : i - 1;
R[i] = i == c ? 0 : i + 1;
U[i] = i;
D[i] = i;
}
}
void insert(int r, int c) {
++tot; ++sz[c];
row[tot] = r; col[tot] = c;
U[tot] = c;
D[tot] = D[c];
U[D[c]] = tot;
D[c] = tot;
if(!hd[r]) {
hd[r] = tot;
L[tot] = tot;
R[tot] = tot;
}
else {
L[tot] = hd[r];
R[tot] = R[hd[r]];
L[R[hd[r]]] = tot;
R[hd[r]] = tot;
}
}
bool dance() {
int c = R[0];
if(!c) return 1;
move(i, R, 0) if(sz[i] < sz[c]) c = i;
remove(c);
++totAns;
move(i, D, c) {
ans[totAns] = row[i];
move(j, R, i) remove(col[j]);
if(dance()) return 1;
move(j, L, i) recover(col[j]);
}
recover(c);
--totAns;
return 0;
}
void print() {
rep(i, 1, totAns) printf("%d ", ans[i]);
}
#undef move
}dlx;
int main() {
scanf("%d%d", &n, &m);
dlx.build(n, m);
rep(i, 1, n) {
rep(j, 1, m) {
scanf("%d", &x);
if(x) dlx.insert(i, j);
}
}
if(dlx.dance()) dlx.print();
else puts("No Solution!");
return 0;
}
时间复杂度
时间复杂度为 \(\mathcal{O}(c^n)\),其中 \(c\) 是一个接近 \(1\) 的常数,\(n\) 是矩阵中 \(1\) 的个数。但 DLX 的常数很小,十分优秀。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号