Codeforces Round 864 (Div. 2) 中文题解
Codeforces Round 864 (Div. 2) 中文题解
A. 李华与迷宫
在 \((x_1,y_1)\) 或 \((x_2,y_2)\) 周围放障碍，更优的那个就是答案。换句话说，定义：
答案为 \(\min\{f(x_1,y_1),f(x_2,y_2)\}\)。
不失一般性，设 \(f(x_1,y_1)\le f(x_2,y_2)\)。由于构造已经给出，答案一定不超过 \(f(x_1,y_1)\)，下证答案不小于 \(f(x_1,y_1)\)。
若 \((x_1,y_1)\) 在角上，我们总可以找到两条从 \((x_1,y_1)\) 到 \((x_2,y_2)\) 且不相交的路径（端点除外）。
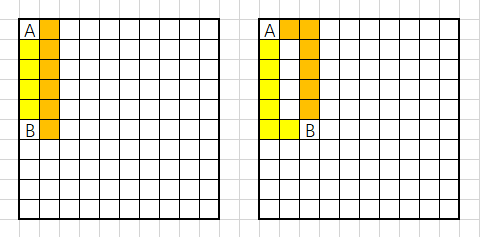
类似地，若 \((x_1,y_1)\) 在边上或在中间，我们总可以找到三条或四条路径。
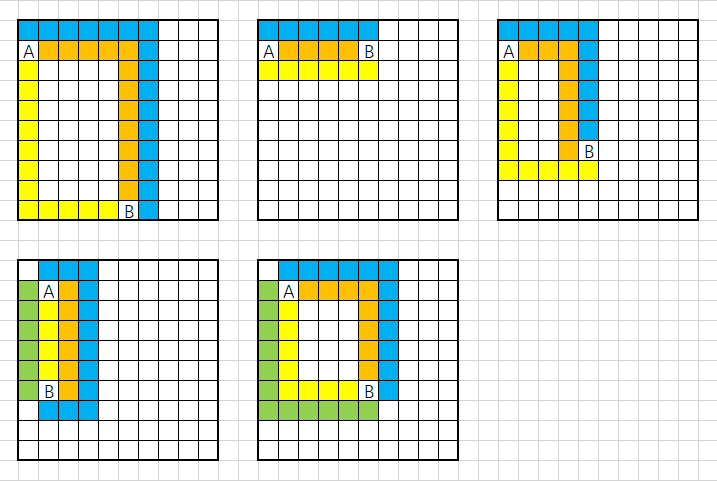
由于路径不相交，我们至少要在每条路径上放一个障碍，因此答案不小于 \(f(x_1,y_1)\)。
综上，答案为 \(f(x_1,y_1)\)。由于我们假设了 \(f(x_1,y_1)\le f(x_2,y_2)\)，原题的答案为 \(\min\{f(x_1,y_1),f(x_2,y_2)\}\)。
时间复杂度 \(\mathcal O(1)\)。
B. 李华与图案
我们枚举每个格子，当颜色与对应格子不同时进行一次操作，可以求出最少需要的操作次数 \(k_{\min}\)。显然，若 \(k < k_{\min}\)，问题无解。
否则，有两种情况：
- 若 \(2\mid n\)，问题有解当且仅当 \(2\mid(k-k_{\min})\)，因为我们必须对应地进行两次操作。
- 若 \(2\nmid n\)，问题恒有解，因为我们可以将剩余的操作都做在正中间。
时间复杂度 \(\mathcal O(n^2)\)。
C. 李华与象棋
首先询问 \((1,1)\) 得到答案 \(k\)。显然，国王一定在这两条线段上：
- \((1,k+1)\) 到 \((k+1,k+1)\)。
- \((k+1,1)\) 到 \((k+1,k+1)\)。
然后，询问 \((1,k+1)\) 和 \((k+1,1)\) 得到答案 \(p,q\)，有三种情况：
- 若 \(p=q=k\)，国王在 \((k+1,k+1)\)。
- 若 \(p < k\)，国王在 \((p+1,k+1)\)。
- 若 \(q < k\)，国王在 \((k+1,q+1)\)。
D. 李华与树
记以 \(x\) 为根的子树为 \(T_x\)。
修改操作并不会对树进行太多的修改。准确地，只有 \(T_{{fa}_x},T_x,T_{{son}_x}\) 的点权和被修改。我们可以暴力维护这些信息。
我们还需要在合理时间内求出一个节点的重儿子。我们用 set 维护每个节点所有儿子的子树大小和编号即可。
时间复杂度 \(\mathcal O((n+m)\log n)\)。
E. 李华与数列（感谢 @N_z_ 的翻译）
记 \(w=\max\limits_{i=1}^n\{a_i\}\)，同时记 \(\varphi^k(x)=\begin{cases}x,&k=0\\\varphi(\varphi^{k-1}(x)),&k\in\mathbb{N}^*\end{cases}\)。
可以证明在经过 \(\mathcal O(\log w)\) 次操作之后，任意的 \(a_i\) 都会变成 \(1\)，之后更多的操作都是没有用的。换句话说，\(\varphi^{\log_2 w+1}(a_i)=1\)。
我们可以构造一棵大小为 \(w\) 的树，它的根是 \(1\)，点 \(k\) 的父亲是 \(\varphi(k)\)，它的高度是 \(\mathcal O(\log w)\)。在一些预处理之后可以在 \(\mathcal O(\log\log w)\) 的复杂度得到任意两点的 LCA。
我们可以使用并查集去维护每个 \(a_i\) 下一个不是 \(1\) 的元素，使用线段树去维护 LCA、最小深度以及区间中的答案。我们可以使用并查集暴力修改，同时在线段树上进行单点更新，查询则是在线段树上进行区间查询。
我们进行势能分析。记 \(\Phi(a_i)\) 是满足 \(\varphi^k(a_i)=1\) 的最小整数 \(k\)。每一次对 \(a_i\) 进行成功操作都会使 \(\Phi(a_i)\) 减去 \(1\)。从而我们可以对 \(a_i\) 进行至多 \(\Phi(a_i)\) 次成功操作。由此，总成功操作次数上限是 \(\sum\limits_{i=1}^n\Phi(a_i)=\mathcal O(n\log w)\)。
对于每一次成功操作，我们访问了 \(\mathcal O(\log n)\) 个在线段树上的节点以及合并了 \(\mathcal O(\log n)\) 两个子树的信息。由于计算 LCA 的时间复杂度，我们需要 \(\mathcal O(\log\log w)\) 来合并信息。所以操作所用的总时间复杂度是 \(\mathcal O(n\log n\log w\log\log w)\)。我们需要在 \(\mathcal O(w)\) 的时间里预处理出 \(\varphi\) 函数以及在 \(\mathcal O(w\log\log w)\) 的时间里预处理倍增数组。我们还需要 \(\mathcal O(\log n\log\log w)\) 来回答每一次询问。
总时间复杂度是 \(\mathcal O(w\log\log w+n\log n\log w\log\log w+m\log n\log\log w)\)。
上面的算法已经足够通过这道题，但是它有着大量的信息合并操作，所以它跑得很慢。
我们考虑线段树不止去维护 LCA，最小深度和区间的答案，我们同时去维护是否 \(\Phi(l_u;r_u)=\sum\limits_{i\in[l_u,r_u]}\Phi(a_i)=0\)。如果我们进入了一个 \(\Phi(l_u;r_u)=0\) 的节点，我们可以忽略它。否则，我们在线段树上递归到叶子然后暴力更新它的信息。
时间复杂度是一样的但是它的效率更高。
挑战：你能在 \(\mathcal O(m\log n)\) 的时间复杂度内解决这个问题吗？
F. 李华与路径
有一个可以通过的 \(\mathcal O(n\log^2n+m)\) 点分治解法，但是正解是 \(\mathcal O(n\log n+m)\) 的重构树。
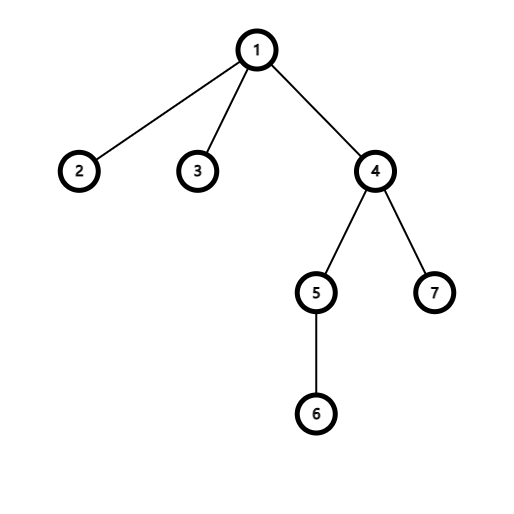
原树如下：
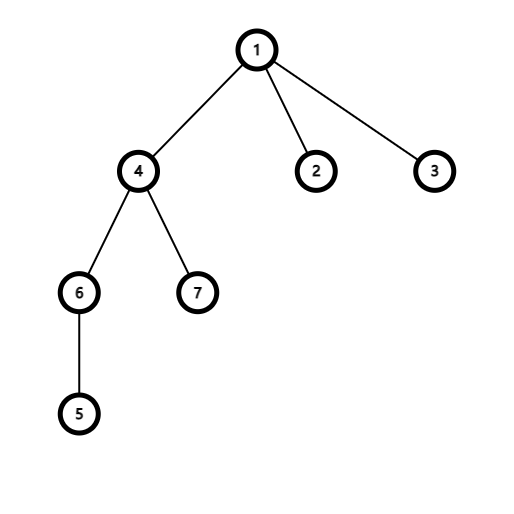
考虑如下的重构树。我们定义两个重构树为小根重构树和大根重构树。
对于大根重构树，我们升序枚举节点。我们在大根重构树中新建节点 \(u\)，然后找到所有在原树中与 \(u\) 邻接的节点 \(v < u\)，令 \(u\) 为 \(v\) 所在重构树根节点的父亲。我们可以使用并查集建出大根重构树。
大根重构树如下图：
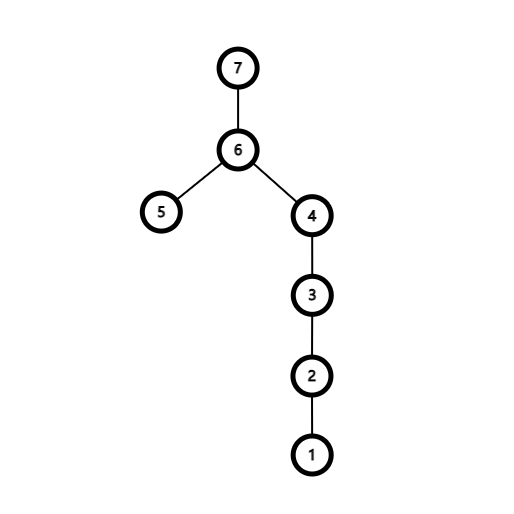
有性质：在大根重构树上的 \(\operatorname{LCA}(u,v)\) 就是原树上 \((u,v)\) 之间路径点的最大编号。
小根重构树与大根重构树类似，如图所示：
在造完轮子之后，我发现这两棵重构树与 Kruskal 重构树有一定关联。这是重构树的另一种理解方式。对于大根重构树，考虑到我们希望求出路径上最大点编号，我们定义 \((u,v)\) 的边权为 \(\max\{u,v\}\)。我们建立最小生成树的 Kruskal 重构树，并将相连的点权相同的节点合并为一个节点。对于小根重构树，定义 \((u,v)\) 的边权为 \(\min\{u,v\}\) 并改用最大生成树的 Kruskal 重构树。
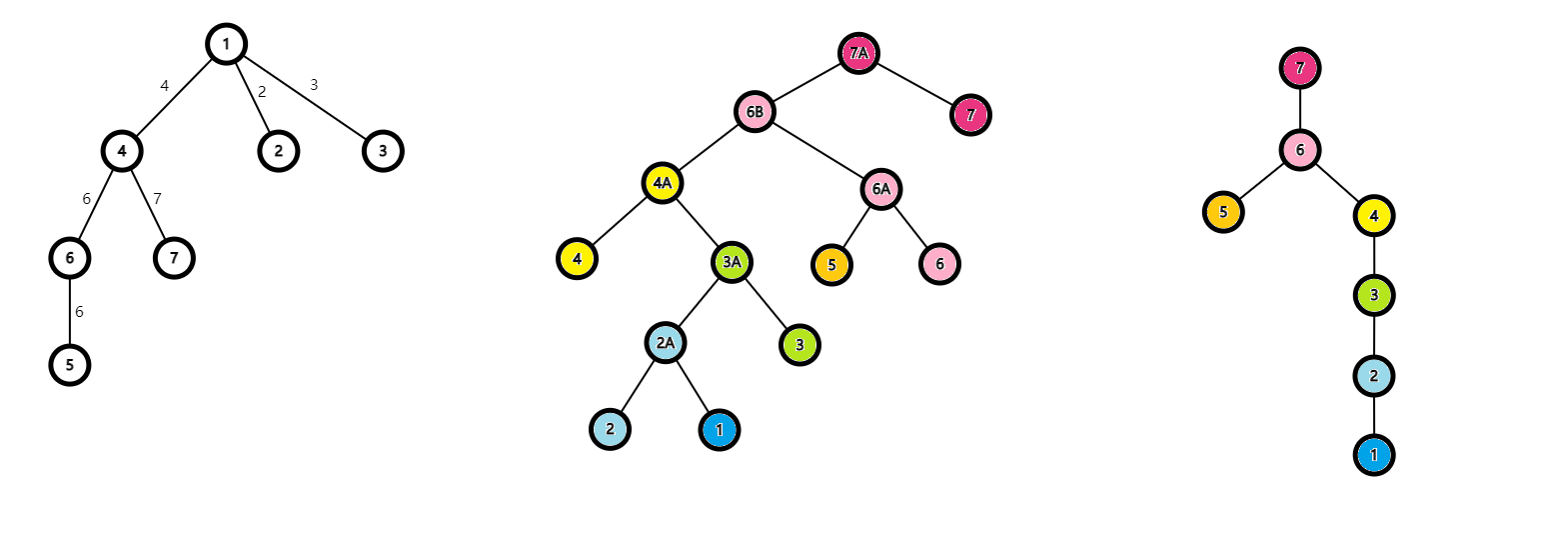
如图为大根重构树和最小生成树的 Kruskal 重构树（左图为重新赋权的图，中图为 Kruskal 重构树，右图为大根重构树）：
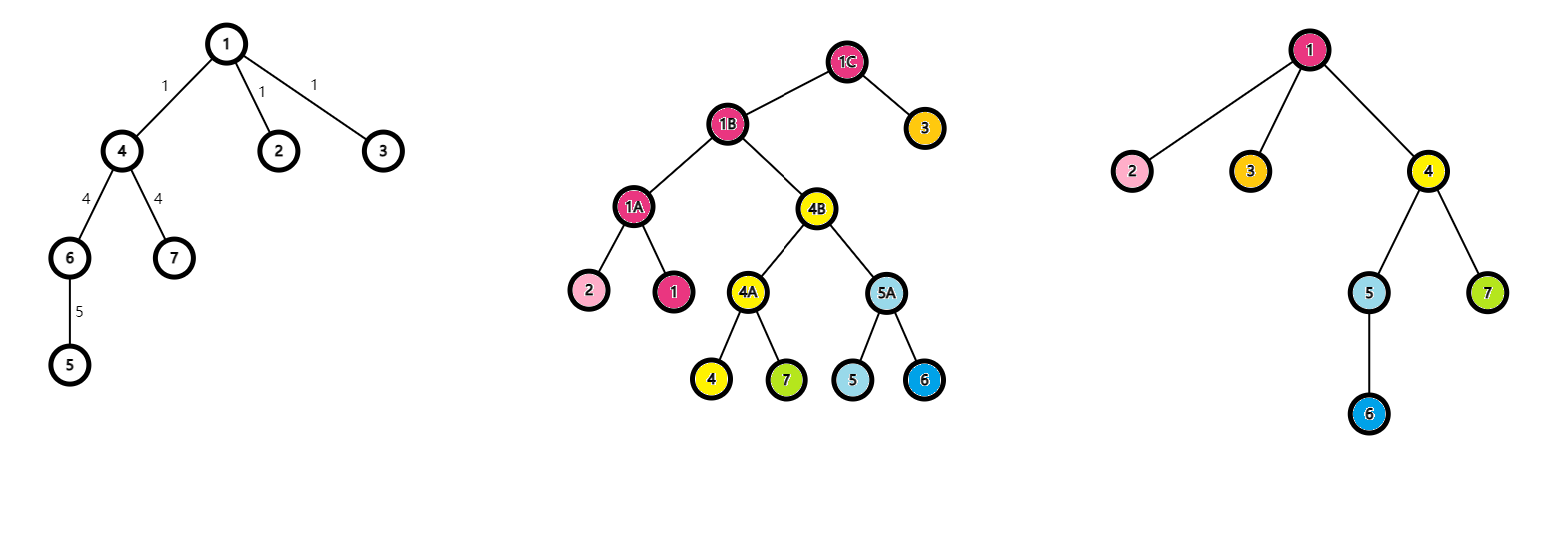
如图为小根重构树和最大生成树的 Kruskal 重构树（左图为重新赋权的图，中图为 Kruskal 重构树，右图为小根重构树）：
下面我们利用两棵重构树解决问题。称两种限制为限制一和限制二。
令 \(K\) 表示满足恰好一个限制的点对个数（即为所求），\(A\) 为满足限制一的点对个数，\(B\) 为满足限制二的点对个数，\(C\) 为同时满足两个限制条件的点对个数。显然有 \(K=A+B-2C\)。
我们利用每个点在两棵重构树上的深度可以容易地计算出 \(A\) 和 \(B\)。由于上述性质，\(C\) 是满足 \(u\) 是小根重构树上 \(v\) 的祖先且 \(v\) 是大根重构树上 \(u\) 的祖先的 \((u,v)\) 数对的数量，利用 DFS 序树状数组即可求出。
最后，我们计算出了最初的答案。如果我们加入了一个编号最大的节点作为叶子，以这个节点为一端的路径自然满足限制二，我们可以使用小根重构树计算以这个节点为终点的不满足限制一的路径数量并更新答案。
时间复杂度： \(O(n\log n+m)\)。
（点分治解法可以参考 Celtic 的评论）
