题解 CF1965E【Connected Cubes】

场切了 1E，第一次上 IGM，纪念一下。

多图警告。

我们称题目中的一个方块为“某色混凝土”。感受一下，发现本题主要的难点在于这些混凝土方块排布得太紧密了，导致容易出现互相遮挡的现象，进而难以构造。于是，我们先思考能否通过一些操作使得这些混凝土互相分离。

如下图的方式可以将每两列混凝土中间插入一列空气：

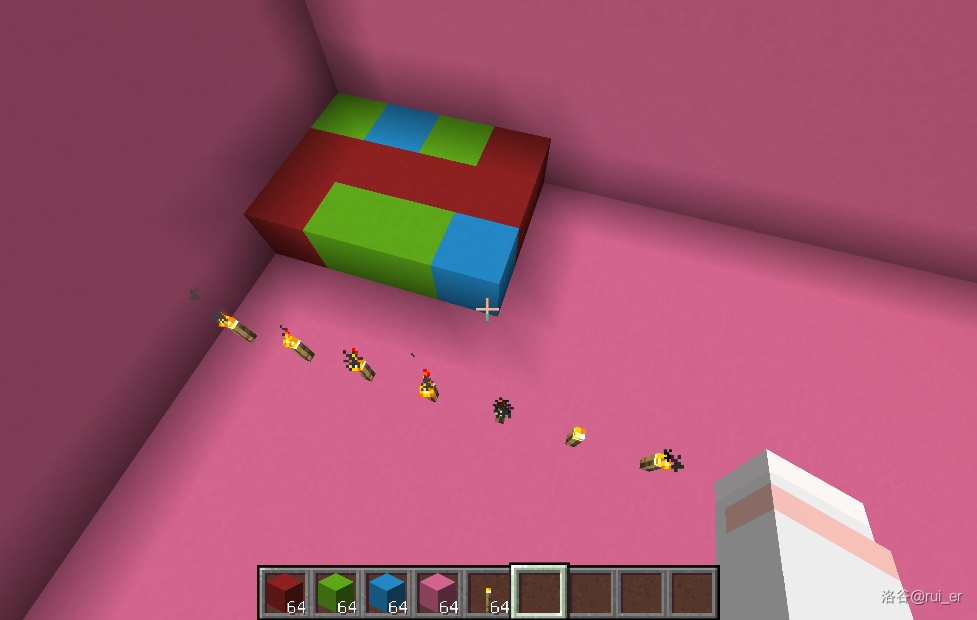
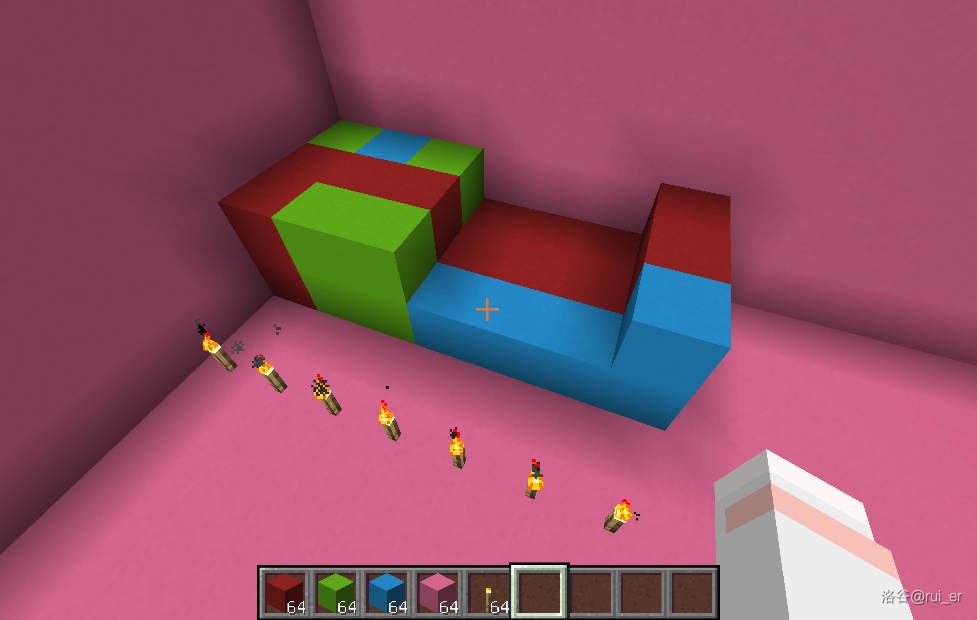
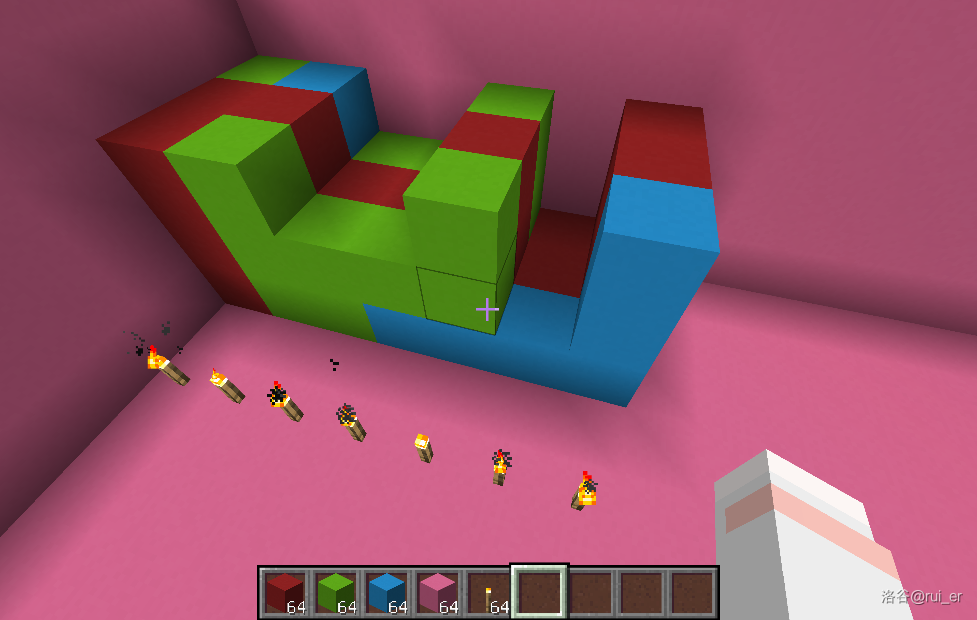
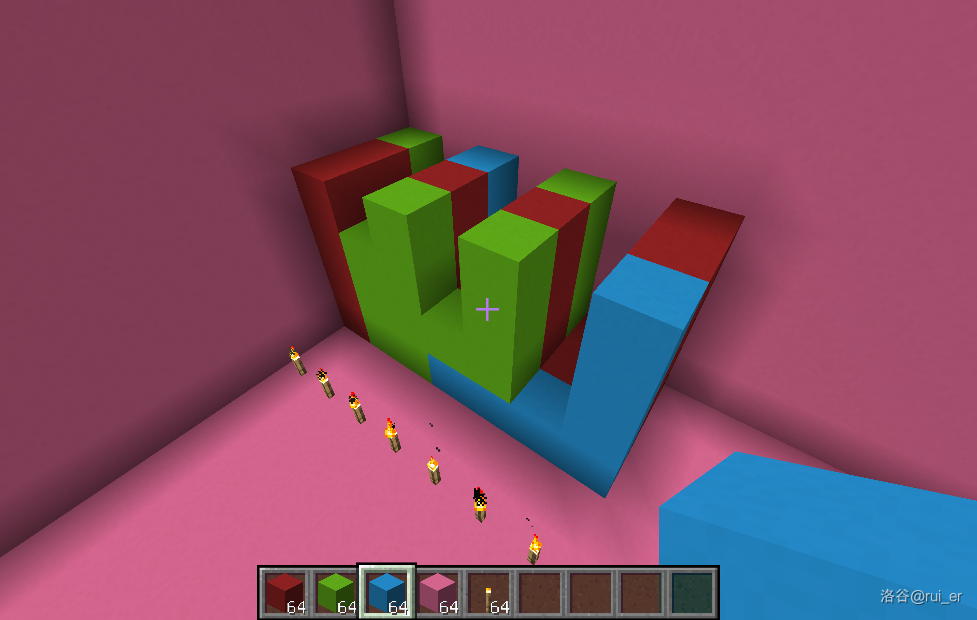
至此，我们在每两列之间都塞了一列空气，且最上层的每块混凝土都显然与最下层对应的混凝土连通。

显然，最上层所有混凝土均至少紧挨着一格空气，我们只需要把所有空气替换成一种颜色的混凝土，那么这种颜色的所有混凝土就连通了：

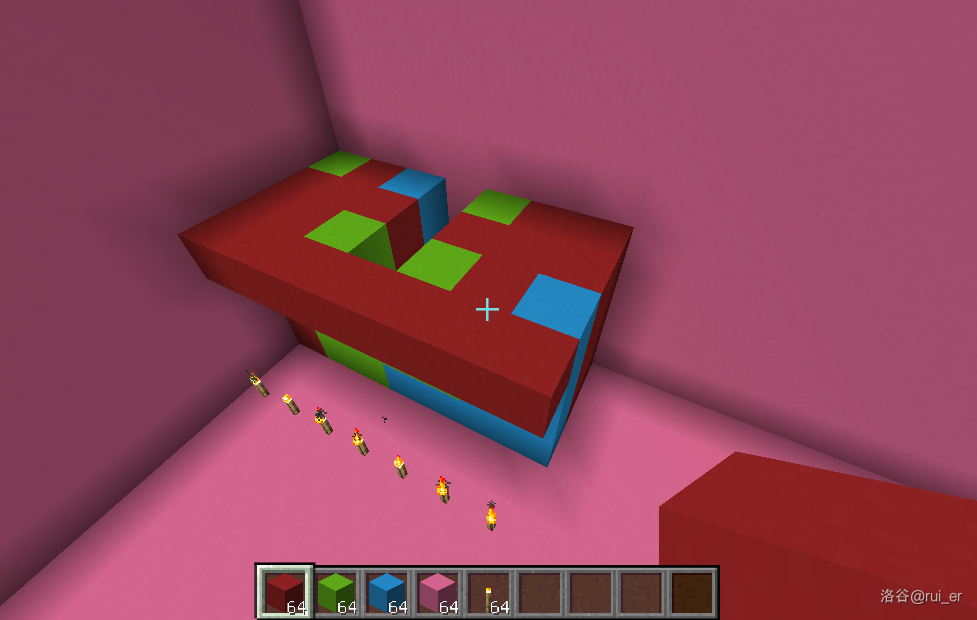
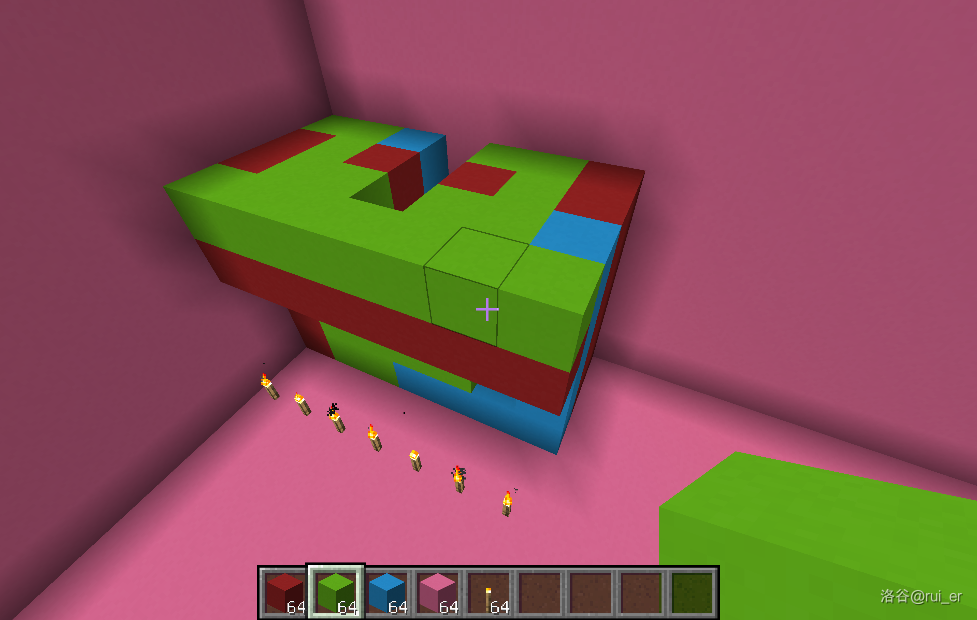
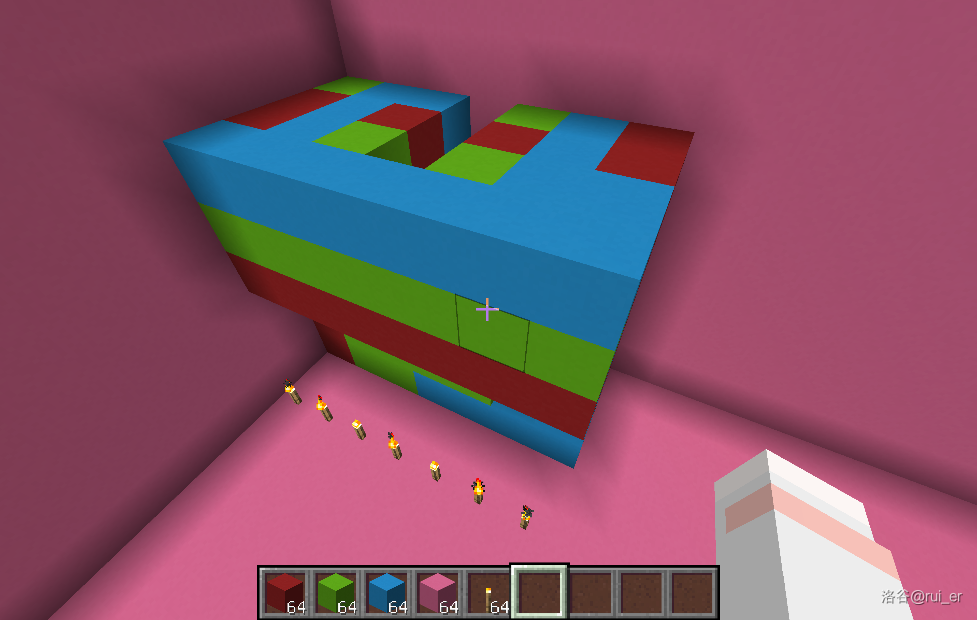
于是就做完了。出于美观考虑，上面示意图中的构造与代码中的构造略有出入，但主要思路完全一致。代码中最坏情况 \(p=373700\)，足以通过本题。这个构造显然还有很大的优化空间，但是我懒了。

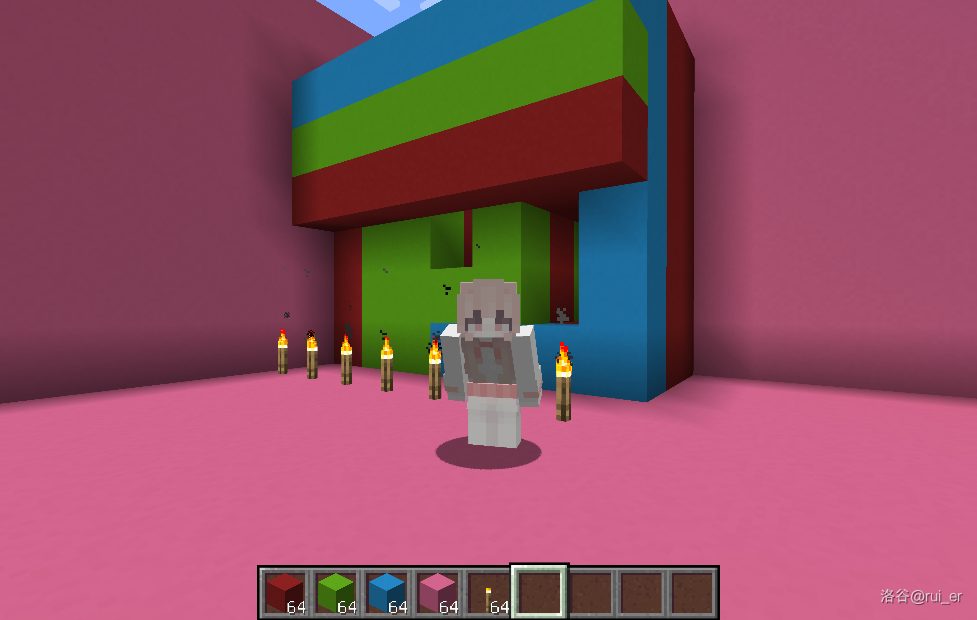
谢谢大家！

// Problem: E. Connected Cubes
// Contest: Codeforces - Codeforces Round 941 (Div. 1)
// URL: https://codeforces.com/contest/1965/problem/E
// Memory Limit: 256 MB
// Time Limit: 4000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x, y, z) for(int x = (y); x <= (z); ++x)
#define per(x, y, z) for(int x = (y); x >= (z); --x)
#define debug(format...) fprintf(stderr, format)
#define fileIO(s) do {freopen(s".in", "r", stdin); freopen(s".out", "w", stdout);} while(false)
#define endl '\n'
using namespace std;
typedef long long ll;

mt19937 rnd(std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now().time_since_epoch()).count());
int randint(int L, int R) {
    uniform_int_distribution<int> dist(L, R);
    return dist(rnd);
}

template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}

template<int mod>
inline unsigned int down(unsigned int x) {
	return x >= mod ? x - mod : x;
}

template<int mod>
struct Modint {
	unsigned int x;
	Modint() = default;
	Modint(unsigned int x) : x(x) {}
	friend istream& operator>>(istream& in, Modint& a) {return in >> a.x;}
	friend ostream& operator<<(ostream& out, Modint a) {return out << a.x;}
	friend Modint operator+(Modint a, Modint b) {return down<mod>(a.x + b.x);}
	friend Modint operator-(Modint a, Modint b) {return down<mod>(a.x - b.x + mod);}
	friend Modint operator*(Modint a, Modint b) {return 1ULL * a.x * b.x % mod;}
	friend Modint operator/(Modint a, Modint b) {return a * ~b;}
	friend Modint operator^(Modint a, int b) {Modint ans = 1; for(; b; b >>= 1, a *= a) if(b & 1) ans *= a; return ans;}
	friend Modint operator~(Modint a) {return a ^ (mod - 2);}
	friend Modint operator-(Modint a) {return down<mod>(mod - a.x);}
	friend Modint& operator+=(Modint& a, Modint b) {return a = a + b;}
	friend Modint& operator-=(Modint& a, Modint b) {return a = a - b;}
	friend Modint& operator*=(Modint& a, Modint b) {return a = a * b;}
	friend Modint& operator/=(Modint& a, Modint b) {return a = a / b;}
	friend Modint& operator^=(Modint& a, int b) {return a = a ^ b;}
	friend Modint& operator++(Modint& a) {return a += 1;}
	friend Modint operator++(Modint& a, int) {Modint x = a; a += 1; return x;}
	friend Modint& operator--(Modint& a) {return a -= 1;}
	friend Modint operator--(Modint& a, int) {Modint x = a; a -= 1; return x;}
	friend bool operator==(Modint a, Modint b) {return a.x == b.x;}
	friend bool operator!=(Modint a, Modint b) {return !(a == b);}
};

const int N = 55;

int n, m, k, a[N][N], px[N][N], py[N][N];
vector<tuple<int, int>> pos[N];
vector<tuple<int, int, int, int>> ans;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n >> m >> k;
    // rep(i, 1, n) rep(j, 1, m) cin >> a[i][j];
    rep(i, 1, n) rep(j, 1, m) a[i][j] = k;
    rep(i, 1, n) rep(j, 1, m) px[i][j] = i, py[i][j] = j;
    rep(z, 1, m) {
        if(z >= 2) {
            rep(i, 1, n) rep(j, 1, m) ans.emplace_back(px[i][j], py[i][j], z, a[i][j]);
        }
        rep(i, 1, n) {
            rep(j, 1, m) {
                if(j == m - z + 1) {
                    int gy = 2 * j - 1;
                    rep(y, j + 1, gy) ans.emplace_back(i, y, z, a[i][j]);
                    px[i][j] = i;
                    py[i][j] = gy;
                }
            }
        }
    }
    int z = m;
    rep(c, 1, k) {
        rep(i, 1, n + 1) {
            rep(j, 1, 2 * m - 1) {
                if(i == n + 1) ans.emplace_back(i, j, z, c);
                else if(j % 4 == 2 || j >= 2 * m - 3 && j % 2 == 0) ans.emplace_back(i, j, z, c);
                else if(int u = a[i][(j + 1) / 2]; (j & 1) && z != m && u >= c) ans.emplace_back(i, j, z, u);
            }
        }
        ++z;
    }
    cout << ans.size() << endl;
    for(auto [x, y, z, c] : ans) cout << x << " " << y << " " << z << " " << c << endl;
    return 0;
}