Linux C语言编程基础练习(使用openeuler)
Linux C语言编程基础练习
1. 选择教材第二章的一节进行编程基础练习
我选择的是2.10节,与链表相关的内容
借此机会我对二叉树以及二叉树的遍历进行了复习,代码如下
#include <stdio.h>
#include<stdlib.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 // 设置最大顶点数为10
#define INFINITY 65535 //将无穷置为65535
typedef int Vertex; //用顶点下标表示顶点
typedef int WeightType; // 边的权值
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; //顶点数
int Ne; //边数
WeightType G[MaxVertexNum][MaxVertexNum]; //邻接矩阵
};
typedef PtrToGNode MGraph;
bool Visited[MaxVertexNum]; //将访问过的顶点标记
MGraph CreateGraph(); //创建图
void Visit( Vertex V )//输出
{
printf(" %d", V);
}
MGraph CreateGraph() //创建图并且将Visited初始化为false
{
int Nv, i, VertexNum;
int v1, v2;
Vertex V, W;
MGraph Graph;
printf("请输入顶点个数:\n");
scanf("%d", &VertexNum);
Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(V = 0; V < Graph->Nv; V ++) {//图的初始化
for(W = 0; W < Graph->Nv; W ++) {
Graph->G[V][W ] = INFINITY;
}
}
printf("请输入边数:\n");
scanf("%d", &Graph->Ne);
if(Graph->Ne) {//当边数不为0时,输入图的顶点元素
for(i = 0; i < Graph->Ne; i ++) {
scanf("%d %d", &v1, &v2);
Graph->G[v1][v2] = 1;//有边置为1,无边置为无穷
Graph->G[v2][v1] = 1;
}
}
return Graph;
}
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) )
{
//从第V个顶点出发递归地深度优先遍历图G
int i;
Visited[V] = true;//标记为true,说明已经遍历过了
Visit(V); //输出此结点
for(i = 0; i < Graph->Nv; i++) //遍历此结点的每个邻接点
{
if(Graph->G[V][i] == 1 && !Visited[i])//有结点且未遍历过
//Graph->G[V][i] == 1说明有结点,!Visited[i]为真,说明未遍历过
{
DFS(Graph, i, Visit); //递归
}
}
}
int main()
{
MGraph G;
Vertex V;
G = CreateGraph();
scanf("%d", &V);
printf("DFS from %d:", V);
DFS(G, V, Visit);
return 0;
}
运行结果如图:
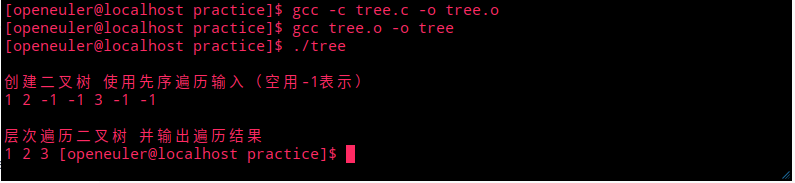
代码思路:

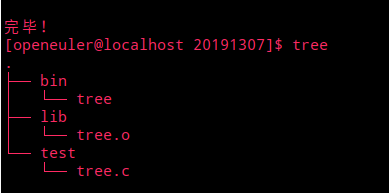
2. 建立自己的项目目录,包含自己学号信息(如20190100linkedlist),构建项目结构(src, include,bin, lib, docs, test...),然后把相应代码和文档放置到正确位置,用tree命令查看项目结构
首先要安装tree相关的文件,命令为:
sudo yum install tree

使用
mkdir命令来创建目录,如图所示

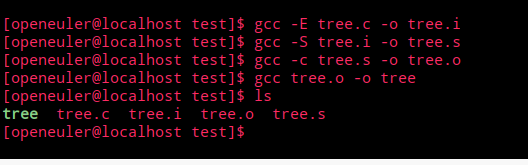
3. gcc相关练习(ESc, iso, -I等)
- 命令如下
gcc -S main.i -o main.s
gcc -c main.s -o main.o
gcc main.o -o main
4.静态库与动态库
此部分练习在myod选做中已经实现
https://www.cnblogs.com/ruier/p/15334074.html
5. 进行gdb相关练习,至少包含四种断点的设置
利用一个简单的循环求和代码来进行断电练习
#include<stdio.h>
#include<stdlib.h>
int main()
{
int i = 1;
int sum = 0;
while (i <= 100) {
sum = sum + i;
i++;
}
printf("1~100的累加求和为%d\n", sum);
return 0;
}
第一次编译后结果为

进行gdb的安装:
sudo yum install gdb
首先生成gdb调试文件
gdb xxx
(1)断点设置

(2)临时断点
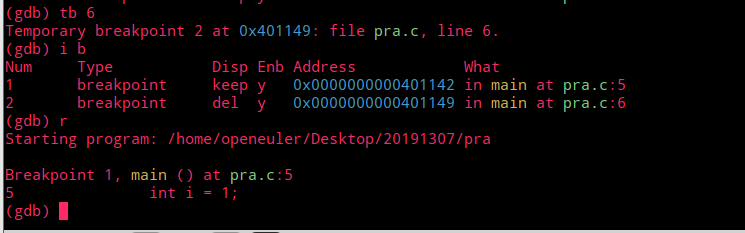
临时断点在程序运行后便会消失
(3)函数断点

(4)条件断点

- 遇到的问题
一开始并没有用gcc -g编译文件,导致gdb文件后无法进行断点设置。
6.编写makefile
在myod选做中使用openEuler练习过具体过程在如下博客中
https://www.cnblogs.com/ruier/p/15334074.html


