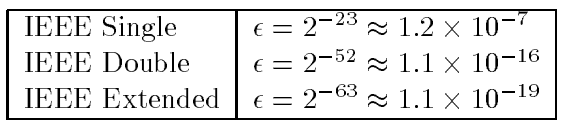Floating point vs Fixed point

1. basic:

reference:

http://blog.leanote.com/post/google-w3dian0/%E5%AE%9A%E7%82%B9%E6%95%B0

http://www.cnblogs.com/cloudseawang/archive/2007/02/06/641652.html

数值数据，分为整数和实数。在计算机中，整数用定点数表示，实数用浮点数表示。

定点数
计算机中采用的一种数的表示方法。参与运算的数的小数点位置固定不变。

定点整数
小数点位固定在最后一位之后称为定点整数。
例：1 111表示-7

定点小数
小数点固定在最高位（即符号位之后）之后称为定点小数。也就是说我们在用“整数”来表示小数。然后通过移位来得到最终的数值。由于存储只使用整数，这个过程会产生误差。

例如：1 111表示-0.875
0.875x2=1.75 --1
0.750x2=1.50 --1
0.500x2=1.00 --1

定点数表达法的缺点在于其形式过于僵硬，固定的小数点位置决定了固定位数的整数部分和小数部分，不利于同时表达特别大的数或者特别小的数。在进行乘法计算的时候，可能需要很多的进行四舍五入。

浮点数（基数隐藏位2）
32位单精度
1位符号s在最高位，8位阶码e在符号位之后，23位尾数。表示范围 [-2^128, 2^128]。

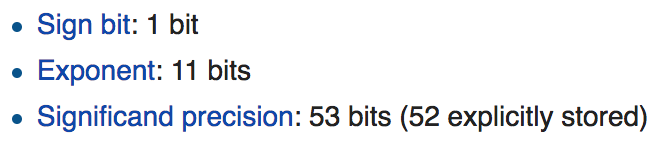
64位双精度
1位符号s，11位阶码e，52位尾数

对于浮点数，有一个事实需要认清楚：在将十进制数转换成二进制数时，并不是所有情况下，都可以把这个十进制在给定的32位或者64位浮点数限制下全部表示出来。对于十进制的小数部分，不断的通过 x2 来得到相应位的数字 (0或者1)，有可能在位数用完的情况下，余数还是不为零。比如无理数。在小结部分，我们可以看到，无论哪种表示，他们的精度都是有最低值的。这种计算过程中误差的累计有可能在最后结果中得到意想不到的结果。

比如在64-位精度下计算 3.46-3.4, 计算结果是：0.06000000000000005。

 

特殊数值：（http://www.cnblogs.com/cloudseawang/archive/2007/02/06/641652.html）

NaN:

无穷（正无穷和负无穷）

零（正零和负零）

非规范化浮点数

 

 小结：