[HNOI2007]紧急疏散EVACUATE(网络最大流+二分答案+BFS)
题目描述
发生了火警,所有人员需要紧急疏散!假设每个房间是一个N M的矩形区域。每个格子如果是'.',那么表示这是一块空地;如果是'X',那么表示这是一面墙,如果是'D',那么表示这是一扇门,人们可以从这儿撤出房间。已知门一定在房间的边界上,并且边界上不会有空地。最初,每块空地上都有一个人,在疏散的时候,每一秒钟每个人都可以向上下左右四个方向移动一格,当然他也可以站着不动。疏散开始后,每块空地上就没有人数限制了(也就是说每块空地可以同时站无数个人)。但是,由于门很窄,每一秒钟只能有一个人移动到门的位置,一旦移动到门的位置,就表示他已经安全撤离了。现在的问题是:如果希望所有的人安全撤离,最短需要多少时间?或者告知根本不可能。
输入格式
第一行是由空格隔开的一对正整数N与M,3<=N <=20,3<=M<=20,
以下N行M列描述一个N M的矩阵。其中的元素可为字符'.'、'X'和'D',且字符间无空格。
输出格式
只有一个整数K,表示让所有人安全撤离的最短时间,
如果不可能撤离,那么输出'impossible'(不包括引号)。
样例
样例输入
5 5
XXXXX
X...D
XX.XX
X..XX
XXDXX
样例输出
3
Solution
二分答案
看到题目不难想到
假设给定一个时间
那么可以验证当前时间内能不能保证所有的人跑出去
显然,时间越长,能跑掉的人越多
所以答案具有单调性
可以进行二分
如果当前时间都可以跑出去
那么考虑适当缩小答案(减少时间)
反之,扩大答案(增加时间)
建图
身为网络流最核心的部分
这道题建图ex死了,加上本人菜死了,足足改了4天
建立超级源点s,超级汇点t
先来说时间对答案的影响
假设现在拥有一个答案时间为\(x\)
那么相当于把每个门拆出来\(x\)个门
保证在x时间内,每个门都能通过一个人
拆出的门按照拆出的编号从小到大依次建边
(比如拆出了1,2,3,那么就1到2,2到3分别建边,边权为inf,表示不受限制)
由于每个人到门的距离不同
所以人应该指向门拆出的第距离个门(md好乱)
没错我知道这句话没人看明白
举个栗子
有一个人他站在坐标7
有一个门它在坐标9
人和门相距距离为3
就是这个图(我把二维拍成一维了)
\(\begin{matrix}
&X &X &X &X \\
&X &. &. &X \\
&D &. &X &X \\
&X &X &X &X
\end{matrix}\)
如果现在二分出一个答案为3
那么就要把坐标9按照某种对应方式(这个对应自己随便编一下,只要保证门编号不重复即可)拆开
由于7号点的人到门的距离为3
那么应该向9拆出的第三个门建边
像这样(右边的点是拆出来的新门)
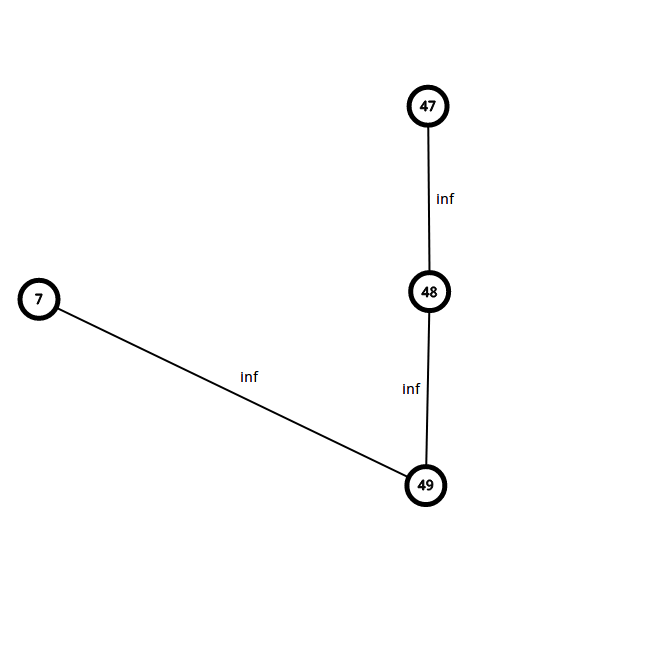
剩下的边就是传统方法了
s到所有人建,边权为1
所有门到t建,边权为1
可以看下样例
在时间为3的时候图长这个样子
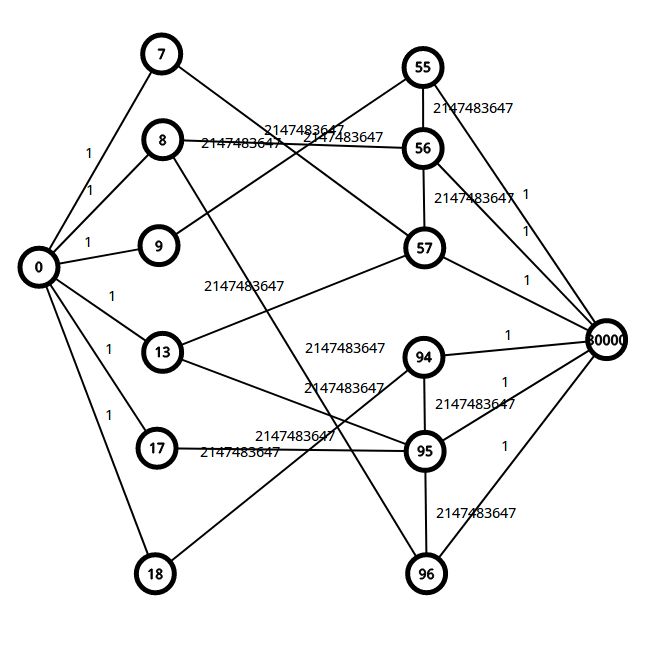
BFS
要预处理出所有人到所有门的距离
bfs扫一遍即可
Code
注 意 细 节
我写的代码比较麻烦
尤其是建边那一块
只要不重不漏,门编号可以简单点不一定非要按照这个写
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#define min(a, b) ({register int AA = a, BB = b; AA < BB ? AA : BB;})
#define inf 0x7fffffff
using namespace std;
inline int read(){
int x = 0, w = 1;
char ch = getchar();
for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return x * w;
}
const int ss = 300005;
const int dx[5] = {0, 1, 0, -1};
const int dy[5] = {1, 0, -1, 0};
struct node{
int to, nxt, w;
}edge[ss];
int head[ss], tot = 1;
inline void add(register int u, register int v, register int w){
edge[++tot].to = v;
edge[tot].nxt = head[u];
edge[tot].w = w;
head[u] = tot;
}
int pre[405][405];
int cur[ss], dis[ss];
bool vis[405][405];
int n, m, s, t;
queue<int> q;
inline bool bfs(register int s){
for(register int i = 0; i <= t; i++)
dis[i] = 0x3f3f3f3f, cur[i] = head[i];
dis[s] = 0;
q.push(s);
while(!q.empty()){
register int u = q.front();
q.pop();
for(register int i = head[u]; i; i = edge[i].nxt){
register int v = edge[i].to;
if(dis[v] == 0x3f3f3f3f && edge[i].w){
q.push(v);
dis[v] = dis[u] + 1;
}
}
}
return dis[t] != 0x3f3f3f3f;
}
inline int dfs(register int u, register int flow){
register int res = 0;
if(u == t) return flow;
for(register int i = cur[u]; i; i = edge[i].nxt){
cur[u] = i;
register int v = edge[i].to;
if(dis[v] == dis[u] + 1 && edge[i].w){
if(res = dfs(v, min(flow, edge[i].w))){
edge[i].w -= res;
edge[i ^ 1].w += res;
return res;
}
}
}
return 0;
}
long long maxflow;
inline long long dinic(){
register long long minflow = 0;
while(bfs(s)){
while(minflow = dfs(s, 0x7fffffff))
maxflow += minflow;
}
return maxflow;
}
inline int change(register int i, register int j){
return (i - 1) * m + j;
}
int a[25][25], person, cnt;
char ch[25];
int l = 1, r = 400;
inline bool check(register int x){
memset(head, 0, sizeof head);
tot = 1;
for(register int i = 1; i <= n; i++)
for(register int j = 1; j <= m; j++)
if(a[i][j] == 1) add(s, change(i, j), 1), add(change(i, j), s, 0);
for(register int i = 1; i <= n; i++){
for(register int j = 1; j <= m; j++){
if(a[i][j] == 2){//门
for(register int id = change(i, j) * x; id < (change(i, j) + 1) * x; id++){
add(id + n * m, t, 1);
add(t, id + n * m, 0);
}
for(register int id = change(i, j) * x; id < (change(i, j) + 1) * x - 1; id++){
add(id + n * m, id + n * m + 1, inf);
add(id + n * m + 1, id + n * m, 0);
}
for(register int p = 1; p <= n; p++){
for(register int q = 1; q <= m; q++)
if(a[p][q] == 1){//人
if(pre[change(p, q)][change(i, j)] <= x){
add(change(p, q), change(i, j) * x + n * m + pre[change(p, q)][change(i, j)] - 1, inf);
add(change(i, j) * x + n * m + pre[change(p, q)][change(i, j)] - 1, change(p, q) ,0);
}
}
}
}
}
}
maxflow = 0;
return dinic() >= person;
}
int st, ed;
queue<pair<int, int> > que;
inline void matrix(register int x, register int y){
que.push(make_pair(x, y));
pre[change(x, y)][change(x, y)] = 0;
while(!que.empty()){
register int xxx = que.front().first, yyy = que.front().second;
que.pop();
for(register int i = 0; i < 4; i++){
register int xx = xxx + dx[i], yy = yyy + dy[i];
if(xx < 0 || xx > n || yy < 0 || yy > m || a[xx][yy] != 1 || vis[xx][yy]) continue;
vis[xx][yy] = 1;
if(pre[change(xx, yy)][change(st, ed)] > pre[change(xxx, yyy)][change(st, ed)] + 1){
que.push(make_pair(xx, yy));
pre[change(xx, yy)][change(st, ed)] = pre[change(xxx, yyy)][change(st, ed)] + 1;
}
}
}
}
signed main(){
memset(pre, 0x3f, sizeof pre);
n = read(), m = read();
for(register int i = 1; i <= n; i++){
scanf("%s", ch + 1);
for(register int j = 1; j <= m; j++){
if(ch[j] == '.') a[i][j] = 1, person++;
else if(ch[j] == 'D') a[i][j] = 2, cnt++;
else a[i][j] = 0;
}
}
for(register int i = 1; i <= n; i++)
for(register int j = 1; j <= m; j++){
if(a[i][j] == 2){
memset(vis, 0, sizeof vis);
st = i, ed = j;
matrix(i, j);
}
}
s = 0, t = 30000;
while(l <= r){
register int mid = l + r >> 1;
if(check(mid)) r = mid - 1;
else l = mid + 1;
}
if(l == 401) puts("impossible");
else printf("%d\n", l);
return 0;
}

