【强化学习RL】model-free的prediction和control — MC, TD(λ), SARSA, Q-learning等
本系列强化学习内容来源自对David Silver课程的学习 课程链接http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching.html
在上一文介绍了RL基础概念和MDP后，本文介绍了在model-free情况下（即不知道回报Rs和状态转移矩阵Pss'），如何进行prediction，即预测当前policy的state-value function v(s)从而得知此policy的好坏，和进行control，即找出最优policy（即求出q*(s, a)，这样π*(a|s)就可以立刻知道了）。
在prediction部分中，介绍了Monto Carlo(MC)，TD(0)，TD(λ)三种抽样(sample)估计方法，这里λ的现实意义是随机sample一个state，考虑其之后多少个state的价值。当λ=0即TD(0)时，只考虑下一个状态；λ=1 时几乎等同MC，考虑T-1个后续状态即到整个episode序列结束；λ∈(0,1)时为TD(λ)，可以表示考虑后续非这两个极端状态的中间部分，即考虑后面n∈(1, T-1)个状态。同时，prediction过程又分为online update和offline update两部分，即使用当前π获得下一个状态的回报v(s')和优化policy π是否同时进行。
在control部分中，介绍了如何寻找最优策略的方法，即找到q*(s, a)。分成on-policy和off-policy两部分，即没有或者是参考了别人的策略（比如机器人通过观察人的行为提出更好的行为）。在on-policy部分，介绍了MC control、SARSA、SARSA(λ)三种方法，off-policy部分介绍了Q-learning的方法。
具体都会在下面正文介绍。
目录：
一、model-free的prediction
1. Monto Carlo(MC) Learning
2. Temporal-Difference TD(0)
3. TD(λ)
二、model-free的control
1. on-policy的Monto Carlo(MC) control
2. on-policy的Temporal-Difference(TD) Learning - SARSA和SARSA(λ)
3. off-policy的Q-learning
一、model-free的prediction
Prediction 部分的内容，全部都不涉及action。因为是衡量当前policy的好坏，只需要估计出每个状态的state-value function v(s)即可。上一文中介绍了使用Bellman Expectation Equation求得某个状态v(s)的数学期望，可以用动态规划DP进行遍历全部状态求得。但是这样的效率是非常低的，下面介绍了两种用sample采样的方法获取v(s)。
1. Monto Carlo(MC) Learning
Monto Carlo是一个经常会遇到的词，它的核心思想是从状态st出发随机采样sample至获得很多个完整序列，可以获得完整序列的实际收益，从而取平均值就是v(st)。需要注意的是，MC只能用于terminate的序列（complete）中。
在MC sample的过程中，每个状态点值函数
，每次遍历N(s)+=1，S(s)为总回报每次S(s)+=Gt,这里Gt表示第t次采样获得的回报，这样当
时，
，所求的平均值V(s)就接近真实值Vπ(s)。在获得完整序列的过程中，很可能会遇到环，即一个状态点经过多次，对此MC有两种处理方法，first step（只在第一次经过时N(s)+=1）和every step（每次经过这个点都N(s)+=1）。
V(s)可以看做所有经过s的回报求和后取平均值产生。但是这个平均值计算不仅可以先求和再做除法，还可以通过在已有的平均值上加一点差值获得，就是下面左式的形式，已有的平均值为V(St)，此次采样获得的回报为Gt，同当前平均值的差值为(Gt - V(St))。但这样来看，需要一直维护一个N(s)计数器，可是，真正平均值优化时只需要知道一个优化的方向即可，所以用一个(0,1)常数α来代替1/N(St)，即下面右式的形式。 α的现实意义是一个遗忘系数，即适当程度以往古老的采样结果，不需要对所有sample出的序列都记得很清楚。
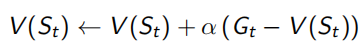
2. Temporal-Difference TD(0)
Monto Carlo采样有一个很明显的缺点，就是必须要sample出完整的序列才能观测出这个序列得到的回报是多少。但是TD(0)这种方法就不需要，它利用Bellman Equation，当前状态收益只和及时回报Rt+1和下一状态收益有关（如下式），红色部分为TD target，α右边括号内为TD error。所以TD(0)只sample出下一个状态点St+1，用已有的policy计算出Rt+1和V(St+1)，这种用已知来做估计的方法叫做bootstrapping(updates a guess towards a guess)，而MC是观测的实际值取平均，是没有bootstrapping的。由于TD(0)只需要sample出下一个状态St+1，所以可以用于non-terminate序列中（incomplete）。
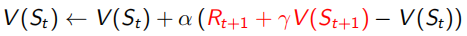
同MC比较，TD(0)采用已有policy预测出TD error，和MC的实际值相比有更大的偏差，但是TD(0)只需要sample出下一个状态序列而不是MC的完整序列，所以TF(0)预测获得的方差比MC小。
具体对v(s)的计算举例如下，进行8次sample，不考虑discount factor γ，下图获得的V(A)和V(B)分别是什么？
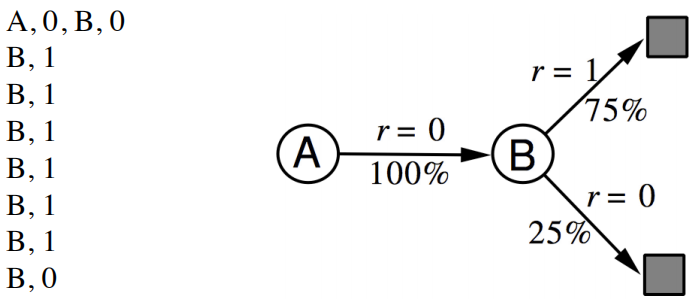
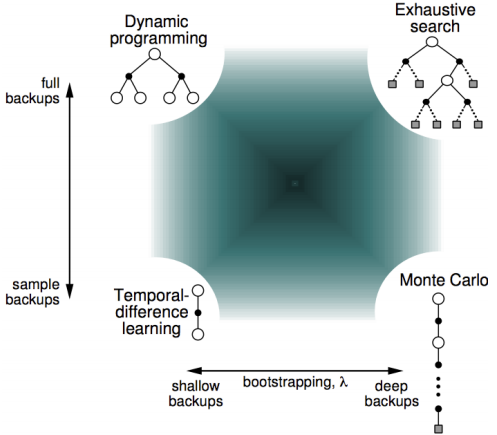
可以看出，无论是TD还是MC，v(B)都是取平均值计算出来的0.75；但是通过MC算出的V(A)是0，因为A只有一次sample结果是0，TD(0)算出来的是0.75，因为A的下一个状态是B且V(B)=0.75, r=0。这一点来看，TD算法更能够利用Markov特性；TD(0)只sample下一个状态点的结果，而不需要每次sample都要等到最终序列结束出结果，所以比MC更高效；但是由于是bootstrapping方法，受初始化值影响更大，拟合性也不如MC好。下图显示了计算期望全部遍历的动态规划DP算法，sample采样下一个状态TD(0)算法，和sample出完整序列T-1个状态的MC算法相互间的关系，但是在1和T-1之间的诸多点，也可以sample考虑，这就是更一般的表达TD(λ)。
3. TD(λ)
这里λ是一个∈[0,1]的实数，它决定了需要采样之后的多少个状态点St+n，n从1到无穷大的简略表达如下左式，Gt(n)表示采样到St+n时获得的回报，那么如何综合一下Gt(1)到Gt(n)的回报呢，这里给每一个Gt乘了一个系数(1-λ)λ^(n-1)，由于∑λ^n = 1/（1-λ），所以右式的∑=1。
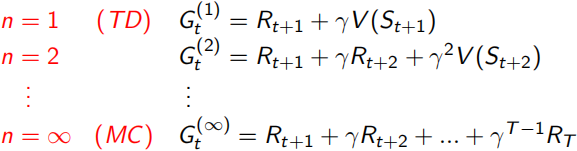
这里Gtλ的系数表示如下图所示，曲线下方的面积和为1。可以看出，每次权重都会削减成原来的λ倍（λ∈[0,1]），这样很靠后的状态权重就逐渐减小，可以达到减小λ减小n的效果，这里控制系数的实数λ就可以控制n，比如λ=0时，与TD(0)的函数表达相同，表示再往后采样一个状态St+1，λ=1时，每次不削减，表示采样到最后相当于MC。
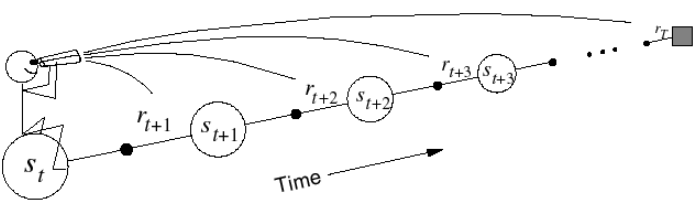
Temporal-Difference的sample分成了forward-view（下图左）和backward-view（下图右）两部分。forward-view就是刚刚叙述的往后sample n个状态点（受λ控制），是看未来的回报的 ，类似于MC只能用于complete的序列。backward-view却可以用在incomplete的序列上，只需在sample的过程中，每一步更新都维护一个Eligibility Trace，记录这个未完毕序列的信息，最后成为对平均值更新的权重。
这里的Eligibility Trace（下面左式），类似于青蛙跳井，每跳一下会升高，不跳的话就逐渐掉下去，既结合了frequency heuristic（跳几下），又结合了recency heuristic（什么时候跳的）。而这里的“跳”，就相当于经过状态所求点s，这样backward-view的值函数更新就可以写成下面右式的形式。当λ=0时，只有在经过s时Et(s)才为1，下面右式 结果同TD(0)表达相同；当λ=1时，整个序列中的每一个状态点有eligibility trace值会被考虑，可以看做MC。每次值函数的更新既参考了TD-error（
）又参考了eligibility trace Et(s)。
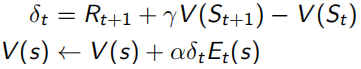
Eligible Trace的函数可以看做如下的表示，纵轴表示积累的值横轴表示时间，| 表示遇到状态s的时刻点：
当λ=0，只在当前状态做更新，下图左式完全等同于TD(0)的下图右式：
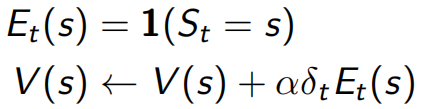
同时，TD(1)完全等同于MC（every-visit）。下面式子可以看出，λ=1时，Et(s)=γ^t-k，连续的TD error求和，为
，即可看作一直sample出完整序列T-1的MC error。
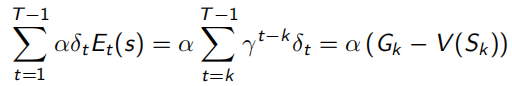
当序列环境是offline update时，即所有sample过程中不改变policy，forward-view和backward-view相同（见下式，左边可以化简到右边的形式），并且TD error可以化为λ-error的形式。
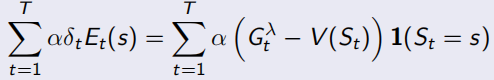
当序列环境是online update时，即边sample边优化policy，backward-view就会一直累积一个error，如下，所以如果访问s多次，这个error就会变得很大。
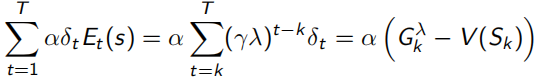
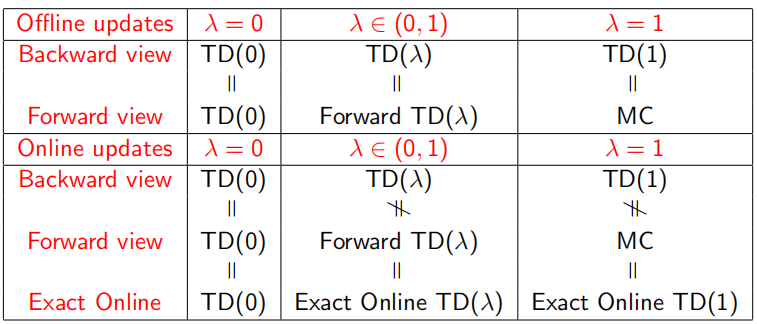
总结的一个表格如下：
二、model-free的control
这里on-policy可以看做“learn on the job”，即对自己行为的反思优化；off-policy可以看做“look over someone‘s shoulder’”，即通过观察其他agent的行为提出优化。
在寻找最优policy过程中，可以看做policy evaluation和policy improvement两部分，一种最基础的贪心算法做improvement如下图。每次V通过当前策略π做evaluation，之后策略π再greedy找寻更优的值函数对应状态，这样可以保证v和π最终都向最优V*和π*收敛。
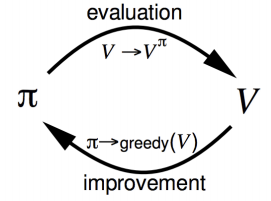
下面介绍的几种方法都是基于这个evaluation和improvement框架进行展开，只不过是model-free的，没有状态转移矩阵P的相关值无法进行
的推导，所以只能用action-value函数q(s, a)，通过
对policy进行优化。
并且，对于下面介绍的sample方法进行policy evaluation来说，单纯用greedy算法并不准确，因为很可能某状态在一个action下会有更高回报，可是正好没有sample到这个更高回报值，该条路径就会被忽略，陷入局部最优解。所以这里又提出使用ε-greedy代替绝对的greedy算法（ε∈[0,1]），变得更soft，每次1-ε概率选择所知最优的action，ε在所有action集合中随机选择，如下面左式，下面右式证明可得，采用ε-greedy获得的Vπ'(s)≥Vπ(s)，整体向更优策略方向走。
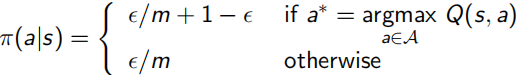
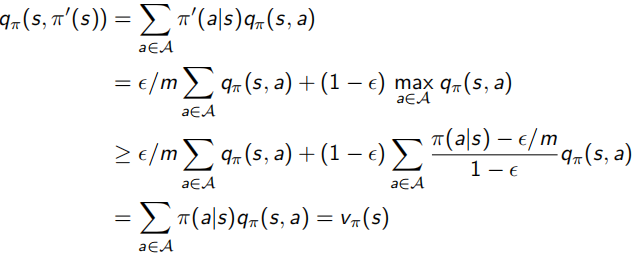
很简单的方法，但可以explore更大的state space，获得更全局的最优解。
1. on-policy的Monto Carlo(MC) control
采用MC方法估计action-value function，然后使用ε-greedy做策略优化。但这里在原始MC control基础上可以做优化，即每次不需要估计出很精确的qπ，只需要Q ≈ qπ即可，再在Q上做优化，仍旧是朝向着最优q*的方向前进的。
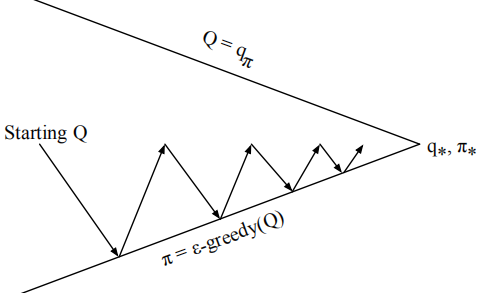
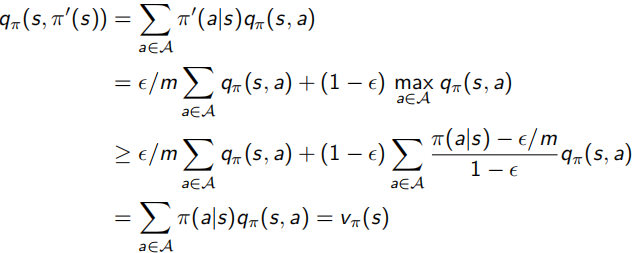
坑代填。。
