【GAN与NLP】GAN的原理 —— 与VAE对比及JS散度出发

 

0. introduction

GAN模型最早由Ian Goodfellow et al于2014年提出，之后主要用于signal processing和natural document processing两方面，包含图片、视频、诗歌、一些简单对话的生成等。由于文字在高维空间上不连续的问题（即任取一个word embedding向量不一定能找到其所对应的文字），GAN对于NLP的处理不如图像的处理得心应手，并且从本质上讲，图片处理相较于NLP更为简单（因为任何动物都可以处理图像，但只有人类可以处理语言）。因而将GAN与NLP结合，具有很深远的影响。Bengio也说，这将是让计算机获得更高智能的关键一步。

在开始之前，有一些先验知识，已经懂的可以跳过。

信息量：“中国队进入了2018世界杯决赛圈”显然比“巴西队进入了2018世界杯决赛圈”发生概率p(x)要低，信息量 I(x)=−log(p(x))要大。

熵（Entropy）：为事件发生所有概率p(xi)的信息量，即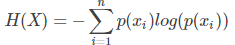

KL（Kullback-Leibler）散度，也叫相对熵，用来衡量真实分布P与预测分布Q之间的差异，即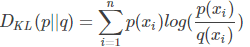，KL散度越小，预测分布越接近于真实分布。需要注意这里DKL(P||Q)!=DKL(Q||P)。

交叉熵（cross entropy），为KL散度拆解后的一部分内容，公式是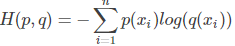。可以看出，相对熵DKL(p||q) = -H(p) + H(p,q)，可以看做负的真实分布p的熵，加p与q交叉熵的结果。

由于p的熵不变，故在机器学习中只需要优化交叉熵作为损失函数即可，以下m为当前batch中样本数，n为标签数。

在单分类问题中（一个节点属于一个类别，使用softmax计算预测数据，每个label累积和为1），损失函数为；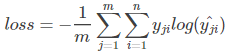

在多分类问题中（一个节点可以属于多个类别，使用sigmoid计算预测数据，每个label独立分布），交叉熵写法可以简化为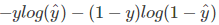，损失函数为。

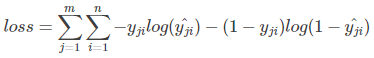JSD（Jensen-Shannon）散度，优化了KL散度中p与q不能换方向的限制，，其中M为P和Q的算数平均数M=1/2*(P+Q)，可以看出，这里P与Q是对称的，JSD(P||Q) = JSD(Q||P)。

 

1. 与VAE对比

Autoencoder的主要思想是，生成内容尽可能和原内容一致。如下图所示，一开始随机生成一个向量作为code，之后通过NN Decoder解码看是否生成对应图片。即原图片input为x，code为z，经过Decoder后output为生成图片x'，其中z要相较于x更小，压缩更多内容。其损失函数由下面所示。VAE是加入高斯噪声的Autoencoder更进一步，进而可以生成更多样的结果。关于Autoencoder和VAE具体可以参见之前文章https://www.cnblogs.com/rucwxb/p/8056144.html  （不参见也可以。。）

  

但是能够生成多样化结果的VAE有一个问题是，它并不是真正的模拟生成真实图片，比如对于同样的7来说，下图的左右和原图都是1个像素点的不同，但右边就是非真实图片，而VAE对于这两个生成图片的处理方法是相同的。

 

 

因而与VAE一步到位、非黑即白的使用重构损失函数的判别方法不同，GAN的判别器对生成器的指导是一步一步地，逐步优化生成器。

 

2. GAN的原理

一般来说，GAN分为Generator和Discriminator，它们有不同的目标，Generator的目标是尽可能train，Discriminator是not train。起初Generator和VAE类似，随机生成一个向量，再由Discriminator判断真假（0/1），之后固定Discriminator，使用gradient descent来更新Generator的参数，使得Discriminator的输出尽可能接近1。

原始GAN的原理是最大似然估计，总体损失函数为，即优化Discriminator使得损失尽可能明显，优化Generator使得损失尽可能缩小。这里G是个函数，输入的是z（一个预先随机设定的标准正态分布，每一轮迭代都会改变），输出的是生成数据x，即G(z)=x，如下图所示。其中，要注意的是优化时改变的不仅是G的参数，还有G。D也是个函数，输入的是x，输出一个x和真实数据的差异（标量）。

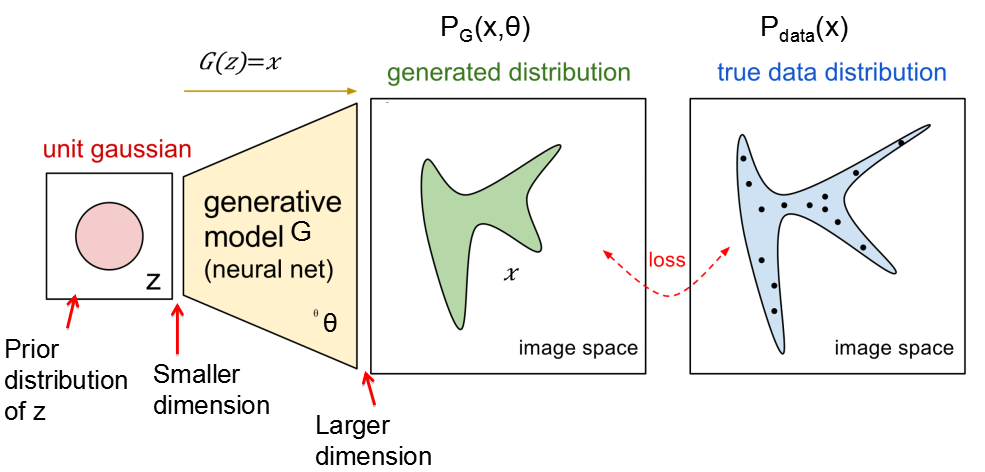
 损失函数V可以看做真实数据分布P_data与生成数据分布P_G的交叉熵（文章开头有详细介绍），即

 

在训练时，先固定G不动，经过k次迭代后找到最优的D。由于对于式子f(D) = alogD + blog(1-D)来说，当D*=a/(a+b)时f(D)有最大值，所以对于上面的函数V来说，D*(x) = Pdata(x) / (Pdata(x)+PG(x)) 时，V(G,D)有最大值，此时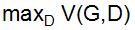可以转换成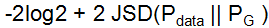的形式，损失函数V(G,D)变成P_data和P_G的JSD距离。

同时，对于Discriminator来说，应该做到输入为真实数据xi时接受，为生成数据x*i时拒绝，V还可以写成这样的形式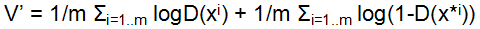，同时，D的目标是maximize这个V，即minimize，这也是Discriminator的损失函数。

对于Generator来说，只需考虑生成数据x*i的情况，因此Generator的损失函数为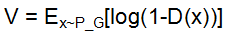，但是由于log(1-D(x))在一开始训练很慢（如下图所示），于是进一步优化Generator的损失函数改为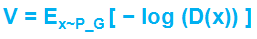

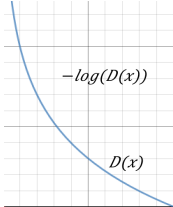
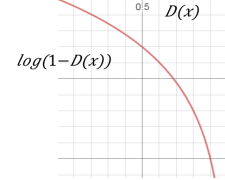
 最终总结下GAN每轮迭代的步骤：

a. 从P_data(x)中采样m个 {x1,x2, … xm} 

b. 通过高斯分布P_prior(z)生成m个{z1, … , zm}

c. 通过x*i=G(zi)获得生成数据 {x*1, … , x*m}

d. 更新Discriminator的参数，以最大化，

　更新方法为梯度下降法θd = θd + ηΔV’(θd) 

a-d重复k次学得Discriminator

e. 通过高斯分布P_prior(z)重新生成m个{z1, … , zm}，并由此生成x*i=G(zi)

f. 更新generator的参数，以最小化，

　更新方法为梯度下降法θg = θg − ηΔV’(θg)

e-f只需重复1次学得Generator

 

3. 训练GAN中遇到的问题 

问题1 —— JS散度=0

Discriminator很快就准确度很接近1，too strong，由于此时还没有训练出很好的Generator（即P_data(x)与P_G(x)在高维空间上几乎没有交叠），生成数据与真实数据完全不同，JSD(P_data||P_G)=0。这样 Discriminator估计的JS散度几乎不会给Generator提供任何信息，使其停止优化。

某种程度上可以通过添加噪声来解决，这样增大P_data(x)与P_G(x)重合面积，使得Discriminator不能完美将P_data(x)与P_G(x)区分开。并且噪声随着时间逐渐减少。

 

问题2 —— Mode Collapse

 

 这个即为只生成一种类型生成数据的情形。如下图所示，红色是生成数据，蓝色是真实数据，由于Discriminator只能提供判断是否生成了正确数据，而对遗失了什么数据不得而知，最终模型会拟合到单一情形中。

 

 

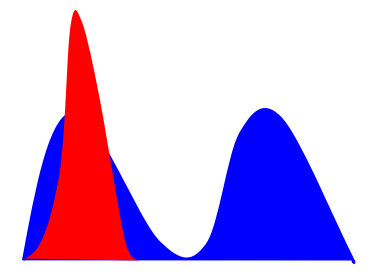
而对于以上两个问题，WGAN都可以解决。

关于WGAN的介绍，知乎上的这篇文章https://zhuanlan.zhihu.com/p/25071913写的很好。

简言之，其修改损失函数，不使用不稳定的JS散度，而是使用Wasserstein距离，即EM（earth-mover）距离，代替了JS散度，解决即使两个分布没有任何重叠情况下对于距离的计算方法，为Generator提供有意义的梯度。

主要在模型上做了四点变化，由于不再使用交叉熵，因而Discriminator最后一层无需sigmoid函数，G与D的损失函数也不取log，另外加入损失函数务必Lipschitz连续的要求，即每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c，使用适合梯度不稳定情况的RMSProp优化器。

 

 

——————— END ———————

之后会继续写出seqGAN等引入强化学习方法将GAN用于NLP领域的文章，敬请期待。