indexOf实现引申出来的各种字符串匹配算法
我们在表单验证时,经常遇到字符串的包含问题,比如说邮件必须包含indexOf。我们现在说一下indexOf。这是es3.1引进的API ,与lastIndexOf是一套的。可以用于字符串与数组中。一些面试经常用问数组的indexOf是如何实现的,但鲜有问如何实现字符串的indexOf是如何实现,因为这是很难很难。要知道,我们平时业务都是与字符串与数组打交道,像数字与日期则更加专业(涉及到二进制,历法)是通过库来处理。
我们回来想一下为什么字符串的indexOf为何如此难?这涉及到前缀与后缀的问题,或更专业的说,你应该想到前缀树或后缀树。如果你连这些概念都没有,你是写不好indexOf。字符串的问题,可以简单理解为遍历,分为全部遍历或跳着查找。
我们看最简单的Brute-Force算法(又被戏称为boyfirend算法)。有两个字符串,长的称之为目标串,短的一般叫模式串。
其算法思想是从目标串的第一个字符串与模式串的第一字符串比较,如果相等,移动目标串的索引,将模式串的索引归零,让目标串的子串与模式串继续逐字比较。

Brute-Force算法
function indexOf(longStr, shortStr, pos) {
var i = pos || 0
/*------------------------------------*/
//若串S中从第pos(S的下标0<= pos <=StrLength(S))个字符起存在和串T相同的子串,则匹配成功。
//返回第一个这样的子串在串S中的下标;否则返回-1
var j = 0;
while (true) {
if (longStr[i + j] == void 0)
break
if (longStr[i + j] === shortStr[j]) {
j++; //继续比较后一个字符
if (shortStr[j] === void 0) {
return i
}
} else {
//重新开始新一轮的匹配
i++;
j = 0;
}
}
return -1; //串S中(第pos个字符起)不存在和串T相同的子串
}
console.log(indexOf('aadddaa', 'ddd'))
KMP算法
第二个是大名鼎鼎的“看毛片”算法,由Knuth,Morris,Pratt三人分别独立研究出来,其对于任何模式和目标序列,都可以在线性时间内完成匹配查找,而不会发生退化,是一个非常优秀的模式匹配算法。它的核心思想是预处理模式串,将模式串构造一个跳转表,有两种形式的跳转表,next与nextval, nextval可以基于next构建,也可以不。
下面这篇文章详KMP 的工件原理,大家有兴趣看看
http://blog.csdn.net/qq_29501587/article/details/52075200
但如何构建next,nextval呢?我搜了许多文章终于找到相关介绍,我汇总在下面的算法中了。
function getNext(str) {
// 求出每个子串的前后缀的共有长度,然后全部整体后移一位,首项为定值-1,得到next数组:
//首先可以肯定的是第一位的next值为0,第二位的next值为1,后面求解每一位的next值时,
//根据前一位的next值对应的字符与当前字符比较,相同,在前一位的next值加1,
//否则直接让它与第一个字符比较,求得共有长度
//比如说ababcabc
var next = [0] //第一个子串只有一个字母,不用比较,没有公共部分,为0
for (var i = 1, n = str.length; i < n; i++) {
var c = str[i]
var index = next[i - 1]
if (str[index] === c) { // a, a
next[i] = index + 1
} else {
next[i] = str[0] === c ? 1 : 0 //第一次比较a, b
}
}
// [0, 0, 1, 2, 0, 1, 2, 0]
next.unshift(-1)
next.pop();
// -1, 0 , 0, 1,2 ,0,1,2
return next
}
function getNextVal(str) {
//http://blog.csdn.net/liuhuanjun222/article/details/48091547
var next = getNext(str)
//我们令 nextval[0] = -1。从 nextval[1] 开始,如果某位(字符)与它 next 值指向的位(字符)相同,
//则该位的 nextval 值就是指向位的 nextval 值(nextval[i] = nextval[ next[i] ]);
//如果不同,则该位的 nextval 值就是它自己的 next 值(nextvalue[i] = next[i])。
var nextval = [-1]
for (var i = 0, n = str.length; i < n; i++) {
if (str[i] === str[next[i]]) {
nextval[i] = nextval[next[i]]
} else {
nextval[i] = next[i]
}
}
return nextval
}
/**
* KMP 算法分三分,第一步求next数组,第二步求nextval数组,第三步匹配
* http://blog.csdn.net/v_july_v/article/details/7041827
*
* 前两步的求法
* http://blog.csdn.net/liuhuanjun222/article/details/48091547
*
*/
function KmpSearch(s, p) {
var i = 0;
var j = 0;
var sLen = s.length
var pLen = p.length
var next = getNextVal(p)
while (i < sLen && j < pLen) {
//①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++
if (j == -1 || s[i] == p[j]) {
i++;
j++;
} else {
//②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
//next[j]即为j所对应的next值
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
console.log(KmpSearch('abacababc', 'abab'))
你可以将这种算法看成DFA (有穷状态自动机)的一种退化写法,但非常晦涩,它是世界第一次打破字符串快速匹配的困局,启迪人们如何跳着匹配字符串了。
Boyer-Moore算法
Boyer-Moore算法是我们文本编辑器进行diff时,使用的一种高效算法,比KMP快三到四倍,思想也是预处理模式串,得到坏字符规则和好后缀规则移动的映射表,下面代码中MakeSkip是建立坏字符规则移动的映射表,MakeShift是建立好后缀规则的移动映射表。
下面是阮一峰的文章,简单介绍什么是坏字符串与好后缀,但没有如何介绍如何实现。
http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
坏字符串还能轻松搞定,但好后缀就难了,都是n^2, n^3的复杂度,里面的循环大家估计也很难看懂。。。
//http://blog.csdn.net/joylnwang/article/details/6785743
// http://blog.chinaunix.net/uid-24774106-id-2901288.html
function makeSkip(pattern) { //效率更高
var skip = {}
for (var n = pattern.length - 1, i = 0; n >= 0; n--, i++) {
var c = pattern[n]
if (!(c in skip)) {
skip[c] = i //最后一个字符串为0,倒二为1,倒三为2,重复跳过
}
}
return skip
}
function makeShift(pattern) {
var i, j, c, goods = []
var patternLen = pattern.length
var len = patternLen - 1
for (i = 0; i < len; ++i) {
goods[i] = patternLen
}
//初始化pattern最末元素的好后缀值
goods[len] = 1;
//此循环找出pattern中各元素的pre值,这里goods数组先当作pre数组使用
for (i = len, c = 0; i != 0; --i) {
for (j = 0; j < i; ++j) {
if (pattern.slice(i, len) === pattern.slice(j, len)) {
if (j == 0) {
c = patternLen - i;
} else {
if (pattern[i - 1] != pattern[j - 1]) {
goods[i - 1] = j - 1;
}
}
}
}
}
//根据pattern中个元素的pre值,计算goods值
for (i = 0; i < len; i++) {
if (goods[i] != patternLen) {
goods[i] = len - goods[i];
} else {
goods[i] = len - i + goods[i];
if (c != 0 && len - i >= c) {
goods[i] -= c;
}
}
}
return goods
}
function BMSearch(text, pattern) {
var i, j, m = 0
var patternLen = pattern.length
var textLen = text.length
i = j = patternLen - 1
var skip = makeSkip(pattern) //坏字符表
console.log(skip)
var goods = makeShift(pattern) //好后缀表
var matches = []
while (j < textLen) { //j 是给text使用
//发现目标传与模式传从后向前第1个不匹配的位置
while ((i != 0) && (pattern[i] == text[j])) {
--i
--j
}
//找到一个匹配的情况
var c = text[j]
if (i == 0 && pattern[i] == c) {
matches.push(j)
j += goods[0]
} else {
//坏字符表用字典构建比较合适
j += Math.max(goods[i], typeof skip[c] === 'number' ? skip[c] : patternLen)
}
i = patternLen - 1 //回到最后一位
}
return matches
}
console.log(BMSearch('HERE IS ASIMPLE EXAMPLE', 'EXAMPLE'))
对于进阶的单模式匹配算法而言,子串(前缀/后缀)的自包含,是至关重要的概念,是加速模式匹配效率的金钥匙,而将其发扬光大的无疑是KMP算法,BM算法使用后缀自包含,从>后向前匹配模式串的灵感,也源于此,只有透彻理解KMP算法,才可能透彻理解BM算法。
坏字符表,可以用于加速任何的单模式匹配算法,而不仅限于BM算法,对于KMP算法,坏字符表同样可以起到大幅增加匹配速度的效果。对于大字符集的文字,我们需要改变坏字符表>的使用思路,用字典来保存模式串中的字符的跳转步数,对于在字典中没有查到的字符,说明其不在模式串中,目标串当前字符直接滑动patlen个字符。
BMH算法
BMH 算法是在BM算法上改进而来,舍弃晦涩复杂的后好缀算法,仅考虑了“坏字符”策略。它首先比较文本指针所指字符和模式串的最后一个字符,如果相等再比较其余m一1个字符。无论文本中哪个字符造成了匹配失败,都将由文本中和模式串最后一个位置对应的字符来启发模式向右的移动。关于“坏字符”启发和“好尾缀”启发的对比,孙克雷的研究表明:“坏字符”启发在匹配过程中占主导地位的概率为94.O3 ,远远高于“好尾缀”启发。在一般情况下,BMH算法比BM有更好的性能,它简化了初始化过程,省去了计算“好尾缀”启发的移动距离,并省去了比较“坏字符”和“好尾缀”的过程。
算法思想:
-
搜索文本时,从后到前搜索;
-
如果碰到不匹配时,移动pattern,重新与text进行匹配;
关键:移动位置的计算shift_table如下图所示。
其中k为Pattern[0 ... m-2]中,使Pattern [ k ] ==Text [ i+m-1 ]的最大值;
如果没有可以匹配的字符,则使Pattern[ 0 ]==Text [ i+m ],即移动m个位置
-
如果与Pattern完全匹配,返回在Text中对应的位置;
-
如果搜索完Text仍然找不到完全匹配的位置,则返回-1,即查找失败
function BMHSearch(test, pattern) {
var n = test.length
var m = pattern.length
var shift = {}
// 模式串P中每个字母出现的最后的下标,最后一个字母除外
// 主串从不匹配最后一个字符,所需要左移的位数
for (var i = 0; i < m - 1; i++) {
shift[pattern[i]] = m - i - 1; //就是BM的坏字母表
}
// 模式串开始位置在主串的哪里
var s = 0;
// 从后往前匹配的变量
var j;
while (s <= n - m) {
j = m - 1;
// 从模式串尾部开始匹配
while (test[s + j] == pattern[j]) {
j--;
// 匹配成功
if (j < 0) {
return s;
}
}
// 找到坏字符(当前跟模式串匹配的最后一个字符)
// 在模式串中出现最后的位置(最后一位除外)
// 所需要从模式串末尾移动到该位置的步数
var c = test[s + m - 1]
s = s + (typeof shift[c] === 'number' ? shift[c] : m)
}
return -1;
}
console.log(BMHSearch('HERE IS ASIMPLE EXAMPLE', 'EXAMPLE'))
console.log(BMHSearch('missipipi', 'pip'))
Sunday算法
Sunday算法思想跟BM算法很相似,在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。如果该字符没有在匹配串中出现则直接跳过,即移动步长= 匹配串长度+1;否则,同BM算法一样其移动步长=匹配串中最右端的该字符到末尾的距离+1。
function sundaySearch(text, pattern) {
var textLen = text.length
var patternLen = pattern.length
if (textLen < patternLen)
return -1
var shift = {} //创建跳转表
for (i = 0; i < patternLen; i++) {
shift[pattern[i]] = patternLen - i
}
var pos = 0
while (pos <= (textLen - patternLen)) { //末端对齐
var i = pos,
j
for (j = 0; j < patternLen; j++, i++) {
if (text[i] !== pattern[j]) {
var c = text[pos + patternLen]
pos += typeof shift[c] === 'number' ? shift[c] : patternLen + 1
break
}
}
if (j === patternLen) {
return pos
}
}
return -1
}
console.log(sundaySearch('HERE IS ASIMPLE EXAMPLE', 'EXAMPLE'))
console.log(sundaySearch('missipipi', 'pip'))
Shift-And和Shift-OR算法
这个算法已经超出笔者的能力,只是简单给出链接
http://www.iteye.com/topic/1130001
bitmap算法思想
这个在腾讯面试题考过,但这个算法优缺点也太明显,本文也简单给出链接,供学霸们研究
http://www.tuicool.com/articles/aYfEvy
更多链接(里面有更多算法实现与复杂度介绍)
http://blog.csdn.net/airfer/article/details/8951802/
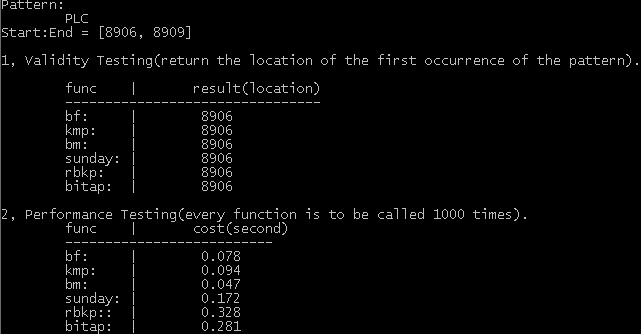
像我们这样的平常人怎么在项目用它们呢,可能在前端比较少用,但也不是没有,如富文本编辑器,日志处理,用了它们性能提升一大截。总之,不要天天做轻松的事,否则你没有进步。

