计算几何基础（入土）知识
施工中。。。
目录
笔记板子向随笔
暂时只有2维，有时间再去弄个三维的
1、一些基础运算函数与结构体定义（部分板子）
2、一些基础的变换公式
一、一些基础运算函数与结构体定义
double pi = acos(-1);
const double eps = 1e-6;
inline int dcmp(double x)//cmp x with 0
{
if (fabs(x) <= eps)return 0;
return x < 0 ? -1 : 1;
}
inline int cmp(double x, double y)
{
//x>y return 1
//x<y reutrn -1
//x==y return 0
return dcmp(x - y);
}
double max(double x, double y)
{
return dcmp(x - y) > 0 ? x : y;
}
double min(double x, double y)
{
return dcmp(x - y) < 0 ? x : y;
}
int sgn(double x)
{
if (fabs(x) < eps)return 0;
else return x < 0 ? -1 : 1;
}
struct Point {
double x, y;
Point() {}
Point(double xx, double yy) { x = xx; y = yy; }
Point operator -(Point s) { return Point(x - s.x, y - s.y); }
Point operator +(Point s) { return Point(x + s.x, y + s.y); }
double operator *(Point s) { return x * s.x + y * s.y; }
Point operator * (double p) { return Point(x * p, y * p); }//向量乘实数
double operator ^(Point s) { return x * s.y - y * s.x; }
Point operator /(double k) { return Point(x / k, y / k); }
bool operator ==(Point s) { return sgn(x - s.x) == 0 && sgn(y - s.y) == 0; }
}p[maxn];
typedef Point Vector;//向量也可以用点表示
double len(Point a) { return sqrt(a * a); }
double dis(Point a, Point b) { return len(b - a); }//两点之间的距离
double Cross(Point a, Point b, Point c)//叉乘,a为公共点
{
return (b - a) ^ (c - a);
}
double Cross(Vector A, Vector B) {
return A.x * B.y - A.y * B.x;
}
double Dot(Point a, Point b, Point c)//点乘 ,a为公共点
{
return (b - a) * (c - a);
}
double Dot(Vector a, Vector b)//点乘 ,a为公共点
{
return a * b;
}
double Angle(Vector A, Vector B) //向量夹角
{
return acos(Dot(A, B) / len(A) / len(B));
}
Vector Rotate(Vector A, double rad) //向量旋转，rad为弧度 且为逆时针旋转的角
{
return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}
Vector Normal(Vector A) //向量A左转90°的单位法向量
{
double L = len(A);
return Vector(-A.y / L, A.x / L);
}
struct Line //直线定义,v为方向向量
{
Point p;
Vector v;
Line(Point p, Vector v) :p(p), v(v) {}
Point point(double t) {//返回直线上一点P = v + (p - v)*t
return v + (p - v) * t;
}
};
//计算两直线交点，调用前需保证 Cross(v, w) != 0
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) //POINT AND VECTOR VERSION
{
Vector u = P - Q;
double t = Cross(w, u) / Cross(v, w);
return P + v * t;
}
Point GetLineIntersection(Line A, Line B) //LINE VERSION
{
Point P = A.p, Q = B.p;
Vector u = P - Q;
Vector v = A.v, w = B.v;
double t = Cross(w, u) / Cross(v, w);
return P + v * t;
}
//点P到直线AB距离公式
double DistanceToLine(Point P, Point A, Point B) {
Vector v1 = B - A, v2 = P - A;
return fabs(Cross(v1, v2) / len(v1));
}//不去绝对值，得到的是有向距离
//点P到线段AB距离公式
double DistanceToSegment(Point P, Point A, Point B)
{
if (A == B)
return len(P - A);
Vector v1 = B - A, v2 = P - A, v3 = P - B;
if (dcmp(Dot(v1, v2)) < 0)
return len(v2);
if (dcmp(Dot(v1, v3)) > 0)
return len(v3);
return DistanceToLine(P, A, B);
}
//点P在直线AB上的投影点
Point GetLineProjection(Point P, Point A, Point B)
{
Vector v = B - A;
return A + v * (Dot(v, P - A) / Dot(v, v));
}
//点是否在线段上
bool OnSegment(Point p, Point a1, Point a2) {
return dcmp(Cross(a1 - p, a2 - p)) == 0 && dcmp(Dot(a1 - p, a2 - p)) < 0;
}
//线段是否相交（不包括端点）
bool Segmentxj(Point a1, Point a2, Point b1, Point b2) {
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1);
double c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
return (sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0);
}
//不包括端点
bool Segmentxjdd(Point a1, Point a2, Point b1, Point b2) {
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1);
double c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
//if判断控制是否允许线段在端点处相交，根据需要添加
if (!sgn(c1) || !sgn(c2) || !sgn(c3) || !sgn(c4)) {
bool f1 = OnSegment(b1, a1, a2);
bool f2 = OnSegment(b2, a1, a2);
bool f3 = OnSegment(a1, b1, b2);
bool f4 = OnSegment(a2, b1, b2);
bool f = (f1 | f2 | f3 | f4);
return f;
}
return (sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0);
}
//多边形有向面积
double PolygonArea(Point* p, int n) {//p为端点集合，n为端点个数
double s = 0;
for (int i = 1; i < n - 1; ++i)
s += Cross(p[i] - p[0], p[i + 1] - p[0]);
return s / 2.0;
}
//判断点是否在多边形内，若点在多边形内返回1，在多边形外部返回0，在多边形上返回-1
int isPointInPolygon(Point p, vector<Point> poly) {
int wn = 0;
int n = poly.size();
for (int i = 0; i < n; ++i) {
if (OnSegment(p, poly[i], poly[(i + 1) % n])) return -1;
int k = sgn(Cross(poly[(i + 1) % n] - poly[i], p - poly[i]));
int d1 = sgn(poly[i].y - p.y);
int d2 = sgn(poly[(i + 1) % n].y - p.y);
if (k > 0 && d1 <= 0 && d2 > 0) wn++;
if (k < 0 && d2 <= 0 && d1 > 0) wn--;
}
if (wn != 0)
return 1;
return 0;
}
struct Circle
{
Point c;//圆心
double r;//半径
Circle(Point c, double r) :c(c), r(r) {}
Point point(double a) {//给出弧度，通过圆心角求坐标
return Point(c.x + cos(a) * r, c.y + sin(a) * r);
}
};
//求圆与直线交点
int getLineCircleIntersection(Line L, Circle C, double& t1, double& t2, vector<Point>& sol) {
double a = L.v.x, b = L.p.x - C.c.x, c = L.v.y, d = L.p.y - C.c.y;
double e = a * a + c * c, f = 2 * (a * b + c * d), g = b * b + d * d - C.r * C.r;
double delta = f * f - 4 * e * g;//判别式
if (sgn(delta) < 0)//相离
return 0;
if (sgn(delta) == 0) {//相切
t1 = -f / (2 * e);
t2 = -f / (2 * e);
sol.push_back(L.point(t1));//sol存放交点本身
return 1;
}
//相交
t1 = (-f - sqrt(delta)) / (2 * e);
sol.push_back(L.point(t1));
t2 = (-f + sqrt(delta)) / (2 * e);
sol.push_back(L.point(t2));
return 2;
}
二、一些基础的（相对于我()）变换公式
1、点积和叉积都满足分配率，点积满足交换律但叉积不满足。
2、向量\((x,y)\)逆时针旋转\(\theta\)得到\((x\cos\theta - y\sin\theta,x\sin\theta + y\cos\theta)\)
3、多边形面积：把多边形顶点按逆时针排序后，\(S = \sum\limits_{i=0}^{n-1}{\overrightarrow{OA_i} \times \overrightarrow{OA}_{(i+1)\bmod n}}\)
4、以A为原点，B为单位点，求点P对于新坐标系的坐标(坐标系变换后的\(\overrightarrow{AB}=(1,0)\))为\(P(x,y)_{new}=(\overrightarrow{AB} \cdot \overrightarrow{AP},\overrightarrow{AB} \times \overrightarrow{AP})*\dfrac{1}{\left|AB\right|^2}\)
5、点P在直线AB上的投影是：\(A+\frac{\overrightarrow{AB}*(\overrightarrow{AB}\cdot\overrightarrow{AP})}{\left|AB\right|^2}\)
6、判断点P与线段AB的关系：
①若\(\overrightarrow{AB}\cdot\overrightarrow{AP}>0\)并且\(\overrightarrow{AB}\cdot\overrightarrow{BP}>0\)，则P在线段AB右侧；
②若\(\overrightarrow{AB}\cdot\overrightarrow{AP}<0\)并且\(\overrightarrow{AB}\cdot\overrightarrow{BP}<0\)，则P在线段AB左侧；
③否则就在线段AB上。
④若\(\overrightarrow{BP}==0\)，则点P在点B上；点A同理。
7、直线与直线的交点、线段与直线、线段与线段
①若两直线平行，则\(\overrightarrow{AB}\times\overrightarrow{CD}==0\)；
②若不平行，则一定有交点，
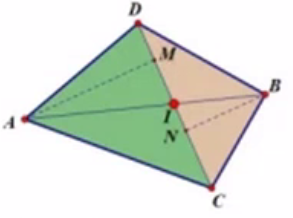
\(\overrightarrow{AI}=\overrightarrow{AB}*\frac{\left|AM\right|}{\left|AM\right|+\left|BN\right|}=\overrightarrow{AB}*\frac{S_{\triangle{ACD}}}{S_{\triangle ACD} \;+S_{\triangle{BCD}}}\)
同理
\(I = A + \overrightarrow{AB} * \frac{\overrightarrow{CD}\times\overrightarrow{CA}}{\overrightarrow{CD}\times\overrightarrow{CA} + \overrightarrow{CB}\times\overrightarrow{CD}} = A +\overrightarrow{AB} * \frac{\overrightarrow{CD}\times\overrightarrow{CA}}{\overrightarrow{AB}\times\overrightarrow{CD}}\)
③直线与线段的交点：先判断两直线交点，再判断线段的端点与交点的位置关系，同侧则没有交点，异侧则有交点；
④线段与线段是否相交：
跨立实验:对于线段\(AB\)和线段\(CD\)，若\((\overrightarrow{AB}\times\overrightarrow{AC}) * (\overrightarrow{AB}\times\overrightarrow{AD}) < 0\)并且\((\overrightarrow{CD}\times\overrightarrow{CA}) * (\overrightarrow{CD}\times\overrightarrow{CB}) < 0\)，则两线段严格相交
严格相交(交点不在端点上)
//线段是否相交（不包括端点）
bool Segmentxj(Point a1, Point a2, Point b1, Point b2) {
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1);
double c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
return (sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0);
}
不严格相交
bool OnSegment(Point p, Point a1, Point a2) {
return dcmp(Cross(a1 - p, a2 - p)) == 0 && dcmp(Dot(a1 - p, a2 - p)) < 0;
}
bool Segmentxjdd(Point a1, Point a2, Point b1, Point b2) {
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1);
double c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
//if判断控制是否允许线段在端点处相交，根据需要添加
if (!sgn(c1) || !sgn(c2) || !sgn(c3) || !sgn(c4)) {
bool f1 = OnSegment(b1, a1, a2);
bool f2 = OnSegment(b2, a1, a2);
bool f3 = OnSegment(a1, b1, b2);
bool f4 = OnSegment(a2, b1, b2);
bool f = (f1 | f2 | f3 | f4);
return f;
}
return (sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0);
}
8、直线与圆
点到直线的距离：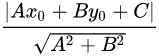
（划掉，用向量做不用开方，误差小一些）
圆心到直线的距离：\(d =\frac{\overrightarrow{AB} \times \overrightarrow{AO}}{\left|\overrightarrow{AB}\right|}\)
