CD from Codeforces Round #701 (Div. 2)

C. Floor and Mod

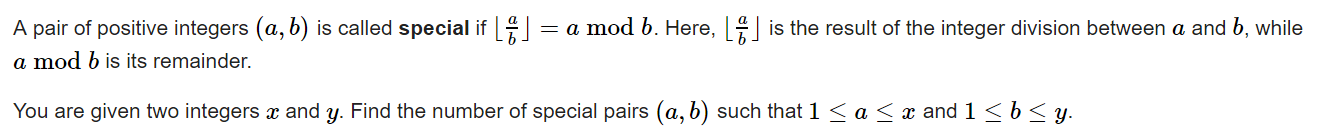
令\(⌊ab⌋=a \% b=k\)，易推导得：若\(x\)满足条件，则\(x=kb+k\)。直接去枚举\(k\)，去构造\(b\)能取值的区间\(lb\)和\(rb\)，\(ans+=rb-lb+1\)。

先构造左区间的\(lb=k+1\),假设左区间合法；去构造右区间的\(rb=b/k-1\)，然后check左右区间是否满足\(lb<=rb\)，如果满足则计入答案，否则直接\(break\)。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pll pair<ll,ll>
#define pii pair<int,int>
#define vll vector<ll>
#define vpll vector<pll>
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
double pi = acos(-1);
const double eps = 1e-9;
const int inf = 1e9 + 7;
const ll lnf = 1e18 + 7;
const int maxn = 1e5 + 10;
ll mod = 1e9 + 7;

int main()
{
	fastio;
	int t;
	cin >> t;
	while (t--)
	{
		ll a, b;
		cin >> a >> b;
		b = min(a, b);
		ll ans = 0;
		for (ll k = 1; k < b; k++)//目的是构造b
		{
			ll lb = k + 1, rb = a / k - 1;
			//左区间的b，右区间的b
			if (k > rb)break;
			rb = min(rb, b);
			ans += rb - lb + 1;
		}
		cout << ans << endl;
	}

	return 0;

}

---

D. Multiples and Power Differences

\(720720 = 2 * 2 * 2 * 2 * 3 * 3 * 5 * 7 * 11 * 13 = lcm(1,2,...,16)\) ，这样所有数的四次方与\(720720\)做差都是1 到 16的倍数。

让\((i+j)\%2=0\)的块为\(720720\)，其余为\(720720-x^4\)

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pll pair<ll,ll>
#define pii pair<int,int>
#define vll vector<ll>
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
double pi = acos(-1);
const double eps = 1e-9;
const int inf = 1e9 + 7;
const ll lnf = 1e18 + 7;
const int maxn = 2e5 + 10;
ll mod = 1e9 + 7;

int main()
{
	fastio;
	//cout << 2 * 2 * 2 * 2 * 3 * 3 * 5 * 7 * 11 * 13 << endl;
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			int x;
			cin >> x;
			if ((i + j) & 1)
				cout << 720720 - x*x*x*x << " ";
			else cout << 720720<<" ";
		}
		cout << endl;
	}
 
	return 0;
 
}