11月刷题记录

①BZOJ1123 BLO（割点）

若选择的点是割点，则通过删除他的边能获得的每个子树的子树大小\(siz\)都与\((n-siz)\)构成答案；所有割出的子树大小和为\(sum\),\((n-sum-1)\)和\(sum+1\)又能构成答案；最后还有该点和其他所有点构成答案\((n-1)\)

若该点不是割点，删除并不会影响图的连通性，所以答案为\(2*(n-1)\)

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)

const int maxn = 1e6 + 10;

struct edge {
	int to, next;
}e[maxn << 1];

int head[maxn], edge_cnt;

inline void add(int from,int to)
{
	e[++edge_cnt] = { to,head[from] };
	head[from] = edge_cnt;
}

int dfn[maxn], low[maxn], num;
ll ans[maxn], siz[maxn];
bool cut[maxn];

int n, m;

void tarjan(int from)
{
	dfn[from] = low[from] = ++num; siz[from] = 1;
	ans[from] = 0;
	int flag = 0;
	ll sum = 0;
	for (int i = head[from]; i != -1; i = e[i].next)
	{
		int to = e[i].to;
		if (!dfn[to])
		{
			tarjan(to);
			siz[from] += siz[to];
			low[from] = min(low[from], low[to]);
			if (low[to] >= dfn[from])
			{
				flag++;
				ans[from] += siz[to] * (n - siz[to]);
				sum += siz[to];
				if (from != 1 || flag > 1)
					cut[from] = 1;
			}
		}
		else
			low[from] = min(low[from], dfn[to]);
	}
	if (cut[from])
		ans[from] += (n - 1) + (n - sum - 1) * (sum + 1);
	else
		ans[from] = 2 * (n - 1);
}

int main() 
{
	fastio;
	cin >> n >> m;
	memset(head, -1, sizeof(head));
	while (m--)
	{
		int x, y;
		cin >> x >> y;
		if (x == y)continue;
		add(x, y), add(y, x);
	}
	num = 0;
	tarjan(1);
	for (int i = 1; i <= n; i++)
		cout << ans[i] << endl;
	return 0;
}

②Mr. Young's Picture Permutations(线性dp)

dp[a][b][c][d][e]表示从第一行到第五行分别的a、b、c、d、e人的合法状态集合的大小，每次转移可以这样理解：
将上一状态所有已排好人的身高全部++，然后在你需要转移的位置（选取的行的末尾）插入一个大小为1的人也合法。
（因为行人数从1到5逐行不升）
状态转移方程：太多了看代码

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)

const int maxn = 1e6 + 10;

ll dp[31][31][31][31][31];

int main()
{
	fastio;
	int k;
	while (cin >> k, k)
	{
		int s[6] = { 0 };
		for (int i = 1; i <= k; i++)cin >> s[i];
        memset(dp,0,sizeof(dp));
		dp[0][0][0][0][0] = 1;
		for (int a = 0; a <= s[1]; a++)
			for (int b = 0; b <= min(a, s[2]); b++)
				for (int c = 0; c <= min(b, s[3]); c++)
					for (int d = 0; d <= min(c, s[4]); d++)
						for (int e = 0; e <= min(d, s[5]); e++)
						{
							ll& x = dp[a][b][c][d][e];
							if (a && a - 1 >= b) x += dp[a - 1][b][c][d][e];
							if (b && b - 1 >= c) x += dp[a][b - 1][c][d][e];
							if (c && c - 1 >= d) x += dp[a][b][c - 1][d][e];
							if (d && d - 1 >= e) x += dp[a][b][c][d - 1][e];
							if (e) x += dp[a][b][c][d][e - 1];
						}
		cout << dp[s[1]][s[2]][s[3]][s[4]][s[5]] << endl;
	}
	return 0;
}

③LCIS(线性dp)

以dp[i][j]并不能表示以a[i]和b[j]结尾的两串的最长LCIS，因为这里为了避免重复转移（如果根据\(LCS\)转移方程当a[i]!=b[j]时\(dp[i][j] = max(dp[i - 1][j],dp[i][j-1])\),当\(a[i]=2,b[j1]=b[j2]=2\)时,会在a[i]==b[j]的转移中重复转移。因此转移只能dp[i][j]=dp[i-1][j]。之前得到的最长dp不一定能转移到dp[n][n].

因此dp[i][j]表示以a1_ai和b1bj可以构成的(以bj为结尾的LCIS)的长度。

只有a[i]==b[j]时才需要从前面找一个合法状态+1取max,合法状态可以记录为val，每次新加入b[j]时当b[j]<a[i]更新val。

对样例dp数组打表：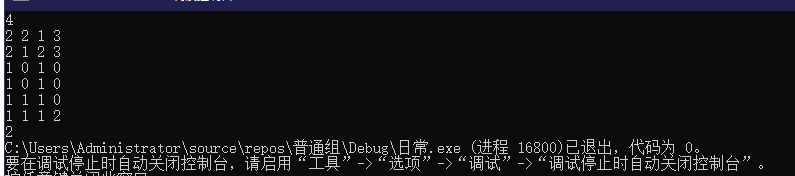

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)

const int maxn = 1e6 + 10;

int dp[3005][3005];

int main()
{
	fastio;
	int n;
	cin >> n;
	vector<int>a(n + 1), b(n + 1);
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	for (int i = 1; i <= n; i++)cin >> b[i];
	int ans = 0;
	for (int i = 1; i <= n; i++)
	{
		int val = 0;
		for (int j = 1; j <= n; j++)
		{
			if (a[i] == b[j])dp[i][j] = val + 1;
			else dp[i][j] = dp[i - 1][j];//为什么不能写max(dp[i - 1][j], dp[i][j - 1])，因为当a[i]=2,b[j1]=b[j2]=2时,会重复转移
			if (b[j] < a[i])val = max(val, dp[i - 1][j]);
			ans = max(ans, dp[i][j]);
		}
	}
	cout << ans;
	return 0;

}

④LUOGU p1006传纸条(线性dp)

当路径不重合时：dp[a][b][c][d] = max(max(dp[a - 1][b][c - 1][d], dp[a - 1][b][c][d - 1]), max(dp[a][b - 1][c - 1][d], dp[a][b - 1][c][d - 1]))+ v[a][b] + v[c][d];

当\(a==c&&b==d\)时只需要将v[a][b]加一次即可，这个重合状态会向下转移，不影响后续的不重合取数

#include <bits/stdc++.h>
using namespace std;

#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)

const int maxn = 1e6 + 10;

int dp[55][55][55][55];
int v[55][55];
int main()
{
	fastio;
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			cin >> v[i][j];
	for(int a=1;a<=n;a++)
		for(int b=1;b<=m;b++)
			for(int c=1;c<=n;c++)
				for (int d = 1; d <= m; d++)
				{
					dp[a][b][c][d] = max(max(dp[a - 1][b][c - 1][d], dp[a - 1][b][c][d - 1]), max(dp[a][b - 1][c - 1][d], dp[a][b - 1][c][d - 1]));
					dp[a][b][c][d] += v[a][b] + v[c][d];
					if (a == c && b == d)dp[a][b][c][d] -= v[a][b];
				}
	cout << dp[n][m - 1][n - 1][m];
	return 0;
}

⑤Mobile Service(线性DP)

如果设计状态dp[i][a][b][c]，复杂度为\(N*L^3\)，显然是会T的。

通过观察可以发现：每次只需移动1人，只需要在状态中记录不动的2个人的位置，另一个人的位置就是上一个请求的位置。
状态转移即:

	dp[i][a][b] = min(dp[i - 1][a][b] + c[last][p], dp[i][a][b]);
	dp[i][a][last] = min(dp[i][a][last], dp[i - 1][a][b] + c[b][p]);
	dp[i][last][b] = min(dp[i][last][b], dp[i - 1][a][b] + c[a][p]);

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL);

const int maxn = 1e5 + 10;

int dp[1010][205][205];
int c[205][205];

int main()
{
	fastio;
	int L, n;
	cin >> L >> n;
	for (int i = 1; i <= L; i++)
		for (int j = 1; j <= L; j++)
			cin >> c[i][j];
	memset(dp, 0x3f, sizeof(dp));
	dp[0][1][2] = dp[0][2][1] = 0;
	int last = 3;
	for (int i = 1; i <= n; i++)
	{
		int p;
		cin >> p;
		for (int a = 1; a <= 200; a++)
		{
			for (int b = 1; b <= 200; b++)
			{
				if (a == b || a == last || b == last)continue;
				dp[i][a][b] = min(dp[i - 1][a][b] + c[last][p], dp[i][a][b]);
				dp[i][a][last] = min(dp[i][a][last], dp[i - 1][a][b] + c[b][p]);
				dp[i][last][b] = min(dp[i][last][b], dp[i - 1][a][b] + c[a][p]);
			}
		}
		last = p;
	}
	int ans = INT_MAX;
	for (int a = 1; a <= 200; a++)
		for (int b = 1; b <= 200; b++)
			ans = min(ans, min(dp[n][a][b], min(dp[n][a][last], dp[n][last][b])));
	cout << ans;
	return 0;

}

⑥AcWing395 冗余路径

将图进行v-dcc缩点，答案即缩点后(度为1的点的数量/2)上取整

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
const int maxn = 1e6 + 10;

int head[maxn], edge_cnt;
struct edge {
    int to, next;
}e[maxn << 1];

inline void add(int from, int to)
{
    e[++edge_cnt] = { to,head[from] };
    head[from] = edge_cnt;
}

int dfn[maxn], low[maxn], num;
int c[maxn], dcc;
bool bridge[maxn << 1];
stack<int>s;

void tarjan(int from, int in_edge)
{
    dfn[from] = low[from] = ++num;
    s.push(from);
    for (int i = head[from]; ~i; i = e[i].next)
    {
        int to = e[i].to;
        if (!dfn[to])
        {
            tarjan(to, i);
            low[from] = min(low[from], low[to]);
            if (low[to] > dfn[from])
                bridge[i] = bridge[i ^ 1] = 1;
        }
        else if (i != (in_edge ^ 1))
            low[from] = min(low[from], dfn[to]);
        //用反向边更新追溯值
    }
    if (dfn[from] == low[from])
    {
        ++dcc;
        while (s.top() != from)
        {
            c[s.top()] = dcc;
            s.pop();
        }
        c[s.top()] = dcc;
        s.pop();
    }
}

vector<int>G[maxn];

int main()
{
    fastio;
    int n, m;
    cin >> n >> m;
    edge_cnt = 1;
    memset(head, -1, sizeof(head));
    while (m--)
    {
        int x, y;
        cin >> x >> y;
        add(x, y);
        add(y, x);
    }
    dcc = 0;
    tarjan(1, -1);

    for (int i = 2; i <= edge_cnt; i++)//遍历每一条边,正反都存
    {
        int x = e[i].to, y = e[i ^ 1].to;
        if (c[x] == c[y])continue;
        G[c[x]].push_back(c[y]);
    }

    int ans = 0;
    for (int i = 1; i <= dcc; i++)
    {
        //cout << i << " " << G[i].size() << endl;
        if (G[i].size()==1)
            ans++;
    }
    cout << (ans + 1) / 2;
    return 0;

}

⑦AcWing1183 电力

求出割点的同时记录能割出多少个dcc,答案=最开始的双连通分量数量+ \(min(flag + (from != root)) - 1\);

对于每个点from，flag为其dfn[from]>=low[to]的数量。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
const int maxn = 1e6 + 10;

int head[maxn], edge_cnt;
struct edge {
    int to, next;
}e[maxn << 1];

inline void add(int from, int to)
{
    e[++edge_cnt] = { to,head[from] };
    head[from] = edge_cnt;
}

int dfn[maxn], low[maxn], root, num, ans, tot;

bool cut[maxn];

void tarjan(int from)
{
    //cout << from << endl;
    dfn[from] = low[from] = ++num;
    int flag = 0;
    for (int i = head[from]; ~i; i = e[i].next)
    {
        int to = e[i].to;
        if (!dfn[to])
        {
            tarjan(to);
            low[from] = min(low[from], low[to]);
            if (low[to] >= dfn[from])
            {
                flag++;
                if (from != root || flag > 1)
                    cut[from] = 1;
            }
        }
        else low[from] = min(low[from], dfn[to]);
        //用反向边更新追溯值
    }
    ans = max(ans, flag + (from != root));
}
int main()
{
    fastio;
    int n, m;
    while (cin >> n >> m, n || m)
    {
        edge_cnt = 1;
        memset(head, -1, sizeof(head));
        memset(dfn, 0, sizeof(dfn));
        ans = tot = num = 0;
        while (m--)
        {
            int x, y;
            cin >> x >> y;
            x++, y++;
            add(x, y);
            add(y, x);
        }
        for (int i = 1; i <= n; i++)
            if (!dfn[i])
            {
                tot++;
                root = i;
                tarjan(i);
            }
        cout<< tot + ans - 1 << endl;
    }

    return 0;

}

CF600E Lomsat gelral（dsu on tree模版）

题意：

有一棵 \(n\) 个结点的以 \(1\) 号结点为根的有根树。
每个结点都有一个颜色，颜色是以编号表示的， \(i\) 号结点的颜色编号为 \(c_i\)
如果一种颜色在以 \(x\) 为根的子树内出现次数最多，称其在以 \(x\) 为根的子树中占主导地位。显然，同一子树中可能有多种颜色占主导地位。
你的任务是对于每一个\(i∈[1,n]\)，求出以 \(i\) 为根的子树中，占主导地位的颜色的编号和。
\(n≤10^5,c_i≤n\)

看上去暴力统计肯定会T。。。

用和轻重链剖分一样方法统计出重儿子，然后去暴力算答案，对于一个节点i：

暴力统计所有子树的贡献

若其为父节点的重儿子，则不需要清空他的贡献；

若其不是重儿子，则清空所有贡献

#include<bits/stdc++.h>
using namespace std;

#define ll long long
const int maxn = 1e5 + 10;
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)

struct edge{
    int to, next;
}e[maxn << 1];

int edge_cnt = 0, head[maxn];

inline void add(int from, int to)
{
    e[++edge_cnt] = { to,head[from] };
    head[from] = edge_cnt;
}

ll col[maxn], ans[maxn], cnt[maxn];

int siz[maxn], son[maxn];

void getson(int from, int fa)//统计重儿子
{
    int MAX = 0;
    siz[from] = 1;
    for (int i = head[from]; ~i; i = e[i].next)
    {
        int to = e[i].to;
        if (to == fa)continue;
        getson(to, from);
        siz[from] += siz[to];
        if (siz[to] > MAX)
            MAX = siz[to], son[from] = to;
    }
}

int Son;

ll sum = 0, MAX = 0;

void add(int from,int fa,int flag)//暴力统计答案
{
    ll &tot = cnt[col[from]];
    tot += flag;
    if (tot > MAX)MAX = tot, sum = col[from];
    else if (tot == MAX)sum += col[from];
    for (int i = head[from]; ~i; i = e[i].next)
    {
        int to = e[i].to;
        if (to == fa || to == Son)continue;
        add(to, from, flag);
    }
}

void dfs(int from, int fa, int opt)//dsu on tree
{
    for (int i = head[from]; ~i; i = e[i].next)
    {
        int to = e[i].to;
        if (to == fa)continue;
        if (to != son[from])dfs(to, from, 0);//先去计算轻儿子的答案
    }
    if (son[from])dfs(son[from], from, 1), Son = son[from];//再去计算重儿子的答案
    //计算完之后：

    add(from, fa, 1), Son = 0;//由于重儿子的答案不会被删除，只需要统计from轻儿子的答案
    ans[from] = sum;//计入答案
    if (!opt)add(from, fa, -1), sum = 0, MAX = 0;//如果这个点不是其父节点的重儿子，则要暴力清空答案
}

int main()
{
    fastio;
    int n;
    cin >> n;
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n; i++)cin >> col[i];
    for (int i = 1; i < n; i++)
    {
        int x, y;
        cin >> x >> y;
        add(x, y);
        add(y, x);
    }
    getson(1, -1);
    dfs(1, 0, 0);
    for (int i = 1; i <= n; i++)
        cout << ans[i] << " ";
    return 0;

}

校oj Teacher Ma专场 H: 闪电五连鞭

最优方案肯定要每次取n-1个，可能有a[i]比较大，需要特判

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
const int maxn = 5e4 + 10;
ll inf = 1e17 + 7;

int main()
{
	fastio;
	int n;
	cin >> n;
	vector<ll>a(n + 1);
	ll MAX = 0;
	ll sum = 0;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		sum += a[i];
		MAX = max(MAX, a[i]);
	}
	sum = (sum + n - 2) / (n - 1);
	cout << max(sum, MAX);

	return 0;

}

校oj Teacher Ma专场 I: 啪的一下，很快的哈

分层图最短路，就直接开个K维嗯转移就没了

这种dij大概不需要记录遍历过的点，毕竟每次贪心取得都是最小的距离，贪心之后不会再被其他的点更新

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fastio ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
const int maxn = 5e4 + 10;
ll inf = 1e17 + 7;

struct edge {
	ll to, cost, next;
}e[maxn<<1];

int edge_cnt = 0, head[maxn];

void add(int from, int to, ll cost)
{
	e[++edge_cnt] = { to,cost,head[from] };
	head[from] = edge_cnt;
}
int S, T, cnt = 0;

struct node {
	ll cost;
	int from;
	int cnt;
	friend bool operator <(node a, node b){
		return a.cost > b.cost;
	}
};

priority_queue<node>q;

ll dis[maxn][11];
int pre[maxn];
ll fee[maxn];
int n, m, K;

void dij(int n)
{
	while (!q.empty())q.pop();
	for (int i = 0; i <= n; i++)
		for (int j = 0; j <= K; j++)
			dis[i][j] = inf;
	dis[S][0] = 0;
	q.push({ 0,S,0 });
	while (!q.empty())
	{
		int from = q.top().from, cnt = q.top().cnt;
		q.pop();
		for (int i = head[from]; ~i; i = e[i].next)
		{
			int to = e[i].to, cost = e[i].cost;
			if (dis[to][cnt] > dis[from][cnt] + cost)
			{
				dis[to][cnt] = dis[from][cnt] + cost;
				q.push({ dis[to][cnt],to,cnt });
			}
			if (cnt < K && dis[to][cnt + 1]>dis[from][cnt])
			{
				dis[to][cnt + 1] = dis[from][cnt];
				q.push({ dis[to][cnt + 1] ,to,cnt + 1 });
			}
		}
	}
}

int main()
{
	fastio;
	memset(head, -1, sizeof(head));
	cin >> n >> m >> K;
	cin >> S >> T;
	while (m--)
	{
		ll x, y, cost;
		cin >> x >> y >> cost;
		add(x, y, cost), add(y, x, cost);
	}
	dij(n);
	ll ans = inf;
	for (int i = 0; i <= K; i++)
		ans = min(ans, dis[T][i]);
	cout << ans;
	return 0;

}

posted @ 2020-11-08 16:20 Lecoww 阅读(87) 评论(0) 编辑收藏举报

刷新页面返回顶部

lecoww disappear forever