打败算法 —— 最长公共子序列
本文参考:
最近重温了下动态规划,看了百度百科以及知乎上的几篇优质解答和文章:
https://www.zhihu.com/question/23995189
https://zhuanlan.zhihu.com/p/72734380
在本篇文章中,讲解最长公共子序列的暴力递归、备忘录和dp数组三种解法
动态规划的基本思想
无后效性:
如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响,即未来与过去无关。这个概念可能比较难以理解,在下面LCS问题的构造最优子结构中再做解释。
最优子结构:
大问题的最优解可以由小问题的最优解推出。
此处动态规划算法与分治法类似,都是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次(暴力递归)。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表或者数组来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。
"寻找最优子结构"也可以直接理解为"寻找状态转移方程",因为找到了当前状态和之前状态关系的方程式,自然也就能看清楚问题的子结构。那么,什么叫做具有"最优"的子结构呢?当其中一个子结构能取到最优解时,其它子结构同样也能取到最优解,各个子结构之间相互独立互不影响,若是一种"此消彼长"的关系,一个子结构取到最优时,影响子结构无法取到最优,则该问题不具备"最优"的子结构。
最长公共子序列问题
从给定的两个序列X和Y中取出尽可能多的一部分字符,按照它们在原序列排列的先后次序排列得到
例如序列 "1 6 8 2 4 6 2" 和 "6 4 2 9 1" 的LCS即为 " 6 4 2"
构造最优子结构
假设当前序列X共有i个字符,序列Y共有j个字符,若序列X的第i个字符和序列Y的第j个字符相同,那么这个字符一定在LCS中,此时如果我们要进一步构建LCS,则需要求解子问题 —— 计算序列X的第1个到第i-1个字符构成的子序列,同序列Y的第1个到第j-1个字符构成的子序列的LCS
即公式 LCS(i, j) = LCS(i - 1, j - 1) + X(i) = LCS(i - 1, j - 1) + Y(j), X(i) == Y(j)
若序列X的第i个字符和序列Y的第j个字符不同,那么就产生两个子问题 —— 我们当前状态的结果要么存在于序列X的第1个到第i-1个字符构成的子序列,同序列Y的第1个到第j个字符构成的子序列的LCS中,要么存在于序列X的第1个到第i个字符构成的子序列,同序列Y的第1个到第j - 1个字符构成的子序列的LCS中
那么我们应该取哪个子问题的解呢?我们无从得知,需要比较二者解的长度,取最大值
即公式LCS(i, j) = Max(LCS(i - 1, j),LCS(i, j - 1)), X(i) != Y(j)
我们并不需要知道两个子问题的解是怎么来的,我们只关心两个子问题的解相比,最大值是哪个,这便是无后效性。同时,因为LCS(i - 1, j),LCS(i, j - 1)两个子问题互相独立,都可以取得最优解,所以具备最优子结构的性质
最后给出一个终止状态,当两个序列都到达尽头时,子问题即为"空"
暴力递归算法
代码:
val firstSeq = "ABCBDAB"
val secondSeq = "YBDCABA"
def lcs(i: Int, j: Int): String = {
if (i < 0 || j < 0) return ""
if (firstSeq(i) == secondSeq(j))
lcs(i - 1, j - 1) + firstSeq(i)
else {
val result1 = lcs(i - 1, j)
val result2 = lcs(i, j - 1)
if (result1.length >= result2.length)
result1
else
result2
}
}
def main(args: Array[String]): Unit = {
println(lcs(firstSeq.length - 1, secondSeq.length - 1))
}
输出:
BCAB
尽管代码十分简洁,并且也能得到正确答案,但是我们可以看到很多子问题可能被重复计算,代码的时间复杂度呈指数级别
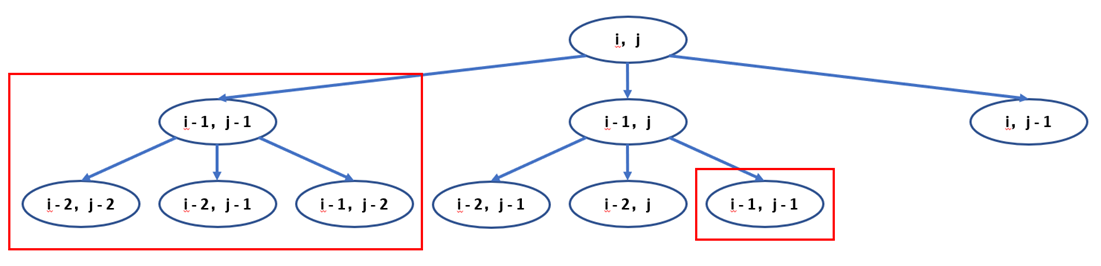
自顶向下的备忘录算法
代码:
val firstSeq = "ABCBDAB"
val secondSeq = "YBDCABA"
def lcs(firstSeq: String, secondSeq: String, i: Int, j: Int, memo: Array[Array[String]]): String = {
if (i == 0 || j == 0) {
return if (firstSeq(i) == secondSeq(j)) firstSeq(i).toString else ""
}
if (firstSeq(i) == secondSeq(j)) {
/*
* 若备忘录有记录,则直接返回
*/
if (memo(i - 1)(j - 1) != null) {
memo(i - 1)(j - 1) + firstSeq(i)
}
/*
* 若备忘录没有记录,则进行递归
*/
else {
memo(i)(j) = lcs3(firstSeq, secondSeq, i - 1, j - 1, memo) + firstSeq(i)
memo(i)(j)
}
} else {
/*
* 同样进行判断,备忘录是否已经存在值
*/
val sub1 = if (memo(i - 1)(j) != null) memo(i - 1)(j) else {
memo(i - 1)(j) = lcs3(firstSeq, secondSeq, i - 1, j, memo)
memo(i - 1)(j)
}
/*
* 同样进行判断,备忘录是否已经存在值
*/
val sub2 = if (memo(i)(j - 1) != null) memo(i)(j - 1) else {
memo(i)(j - 1) = lcs3(firstSeq, secondSeq, i, j - 1, memo)
memo(i)(j - 1)
}
if (sub1.length > sub2.length) {
memo(i)(j) = sub1
} else {
memo(i)(j) = sub2
}
memo(i)(j)
}
}
def main(args: Array[String]): Unit = {
val memo = Array.ofDim[String](firstSeq.length, secondSeq.length)
println(lcs(firstSeq, secondSeq, firstSeq.length - 1, secondSeq.length - 1, memo))
for (i <- memo.indices) {
for (j <- memo(i).indices)
print(f"${memo(i)(j)}%-8s")
println()
}
}
输出:
BDBA
|
null |
null |
A |
null |
null |
||
|
null |
B |
B |
B |
B |
null |
null |
|
B |
B |
BC |
BC |
null |
null |
|
|
null |
B |
B |
BC |
BC |
BCB |
null |
|
null |
null |
BD |
BD |
BD |
BCB |
null |
|
null |
null |
null |
null |
null |
null |
BCBA |
|
null |
null |
null |
null |
null |
BDAB |
BDAB |
尽管通过备忘录的"剪枝",解决了暴力递归中重复计算子问题的弊端,但是由于自顶向下的递归,任然造成不必要的函数现场保存的开销,因此引入自底向上的递推算法
自底向上的dp数组算法(数组保存字符序列本身)
代码:
val firstSeq = "ABCBDAB"
val secondSeq = "YBDCABA"
def lcs(firstSeq: String, secondSeq: String): Array[Array[String]]
= {
val dp = Array.ofDim[String](firstSeq.length + 1, secondSeq.length + 1)
/*
* base case
*/
for (i <- dp.indices) dp(i)(0) = ""
for (j <- dp(0).indices) dp(0)(j) = ""
for (i <- 1 until dp.length) {
for (j <- 1 until dp(i).length) {
if (firstSeq(i - 1) == secondSeq(j - 1))
dp(i)(j) = dp(i - 1)(j - 1) + firstSeq(i - 1)
else
dp(i)(j) = if (dp(i - 1)(j).length > dp(i)(j - 1).length) dp(i - 1)(j) else dp(i)(j - 1)
}
}
dp
}
def main(args: Array[String]): Unit = {
val dp = lcs(firstSeq, secondSeq)
for (i <- dp.indices) {
for (j <- dp(i).indices) {
if (dp(i)(j) == "")
print(f
