数据库学习摘记 —— 关系模式的函数依赖
关系与关系模式的联系:
关系模式是相对稳定的,静态的,是把所有元组删去后的一张空表格,是对元组数据组织方式的结构描述,而关系却是动态变化的,不稳定的,是将若干元组填入关系模式后得到的一个取值实例。每一个关系对应一个关系模式,每一个关系模式可以定义多个关系。
关系模式R(U)对应的具体关系通常用小写字母r来表示。
函数依赖:
设R(U)是属性集U={A1, A2, …, An}上的关系模式,X和Y是U的子集。若对R(U)的任一具体关系r中的任意两个元组t1和t2,只要t1[X]=t2[X] 就有t1[Y]=t2[Y]。则称"X函数确定Y" 或"Y函数依赖于X",记作X→Y,X为这个函数依赖的决定因素。
函数依赖要求R(U)的一切具体关系r都要满足的约束条件。
若X→Y且Y→X,则记作X⇿Y
平凡函数依赖:X→Y,Y⊆X // 对于任一关系模式,平凡函数依赖必然是成立的
非平凡函数依赖:X→Y,Y⊄X
完全函数依赖:
如果X→Y,且对于X的任何一个真子集X',都有X不函数确定Y ,则称Y对X完全函数依赖或者X完全决定Y,记作: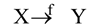
部分函数依赖:
如果X→Y,但Y不是完全函数依赖于X,则称Y 对X部分函数依赖,记作: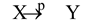
传递函数依赖:
如果X→Y,Y→Z,且 Y→X,Y⊄X,Z⊄Y,则称Z对X传递函数依赖,记作:
候选键:
对关系模式R(U),设K⊆U,且K完全函数确定U,则K为能够唯一确定关系中任何一个元组(实体)的最少属性集合,称K为R(U)的候选键或候选关键字。
【R(U,F),U={ A,B,C,D,E,G },F={AB→C,CD→E,E→A,A→G},求候选键】
因G只在右边出现,所以G一定不属于候选码
而B,D只在左边出现,所以B,D一定属于候选码
BD的闭包还是BD,则对BD进行组合,除了G以外,BD可以跟A,C,E进行组合
先看ABD
ABD本身自包ABD,而AB→C,CD→E,A→G,所以ABD的闭包为ABDCEG=U
再看BDC
CD→E,E→A,A→G,BDC本身自包,所以BDC的闭包为BDCEAG=U
最后看BDE
E→A,A→G,AB→C,BDE本身自包,所以BDE的闭包为BDEAGC=U
因为(ABD)、(BCD)、(BDE)的闭包都是ABCDEG所以本问题的候选码有3个分别是ABC、BCD和BDE
主键:
通常在R(U)的多个候选键中任意选定一个候选键作为主键,也称为主码或主关键字。
当关系模式的属性全体是候选键时,属性全体也就是主键,可称为全键或全码。
主属性与非主属性:
对关系模式R(U),包含在任何一个候选键中的属性称为主属性,不包含在任何候选键中的属性称为非主属性或非码属性。
外键:
对关系模式R(U),设X⊆U。若X不是R(U)的主键,但X是另一个关系模式的主键,则称X是R(U)的外键或外部关键字。
函数依赖的逻辑蕴涵:
对于满足函数依赖集F的关系模式R(U,F)的任意一个具体关系r,若函数依赖X→Y都成立,则称F逻辑蕴涵X→Y,记为F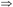 X→Y。
X→Y。
若在F中没有X→Y函数依赖,但可以通过F中的现有函数依赖推导得出X→Y,则也记F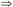 X→Y。
X→Y。
F的闭包:
被函数依赖集F逻辑蕴涵的函数依赖所构成的集合,称为F的闭包,记作F+。即:F+={X→Y | F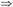 X→Y}。显然F⊆ F+
X→Y}。显然F⊆ F+
函数依赖完备集:
当函数依赖集F= F+
Armstrong公理系统:
自反律:如果Y⊆X⊆ U,则X→Y成立,即F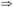 X→Y。
X→Y。
增广律:如果X→Y成立,则XZ→YZ 成立(XZ是X∪Z的简单记法),即若F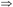 X→Y,则F
X→Y,则F XZ→YZ。
XZ→YZ。
传递律:如果X→Y,Y→Z成立,则X→Z成立,即若F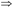 X→Y,F
X→Y,F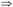 Y→Z,则F
Y→Z,则F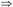 X→Z。
X→Z。
合并律:如果X→Y和X→Z成立,那么X→YZ成立,即若F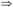 X→Y,F
X→Y,F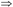 X→Z,则F
X→Z,则F X→YZ。
X→YZ。
伪传递律:如果X→Y和WY→Z成立,那么WX→Z成立,即F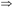 X→Y,F
X→Y,F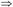 WY→Z,则F
WY→Z,则F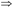 WX→Z。
WX→Z。
分解律:如果X→Y和Z⊆Y成立,那么X→Z成立,即若F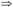 X→Y,Z⊆Y,则F
X→Y,Z⊆Y,则F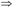 X→Z。
X→Z。
推论:对关系模式R(U),设X⊆U,{A1, A2 ,…,Am}⊆U,则X→{A1, A2 ,…, Am}成立的充分必要条件是
X→Ai (i=1,2,…,m)成立。
属性集X关于F的闭包X+F :
![]()
显然X⊆X+F⊆U
闭包的计算:
设F是属性集U上的函数依赖集,X,Y 是U的子集,则X→Y能由F根据Armstrong公理导出的充分必要条件是 Y⊆X+。
【设关系模式R(U),其属性集上函数依赖:F={AB→C, B→D, C→E, EC→B, AC→B},令X={A, B},求X+】
解:
第1次:
X(0)= Ø,X(1)={A, B},F= Ø
由于X(0)≠X(1),令X(0)=X(1)={A, B}
函数依赖集F'={ AB→C, B→D},令F=F-F'={C→E, EC→B, AC→B},
将F'中的每一个函数依赖的右端属性C,D并入X(1)中,即令X(1)={A, B}∪{C, D}={A, B, C, D}
第2次:
由于X(0)≠X(1),令X(0)=X(1)= {A, B, C, D};
函数依赖集F'={C→E, AC→B},令F=F-F'={EC→B}
将F'中的每一个函数依赖的右端属性E, B并入X(1)中,即令X(1)={A, B, C, D }∪{E, B}={A, B, C, D, E}
第3次:
由于X(0)≠X(1),令X(0)=X(1)= {A, B, C, D, E }
函数依赖集F'={EC→B},令F=F-F'= Ø
将F'中的每一个函数依赖的右端属性B并入X(1)中,即令X(1)={A, B, C, D, E }∪{B}={A, B, C, D, E}
第4次:
由于X(0)=X(1),输出X(1)={A, B, C, D, E}=X+
{A,B}→U={A, B, C, D, E},由于{A}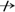 U,{B}
U,{B}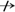 U,所以{A,B}是侯选键
U,所以{A,B}是侯选键
函数依赖集的等价与覆盖:
如果G+=F+,就说函数依赖集F与G等价,且F覆盖G,G覆盖F,它的充分必要条件是F⊆G+ ,G⊆F+
每个函数依赖集F都可以被一个右部只有单属性的函数依赖集G所覆盖。
最小函数依赖集,也称为最小依赖集或最小覆盖:
F中任一函数依赖的右部仅含有一个属性。
F中不存在这样的函数依赖X→A,使得F与F-{X→A}等价。 // 右部没有冗余的函数依赖
F中不存在这样的函数依赖X→A,X有真子集Z使得F-{X→A}∪{Z→A}与F等价。 // 左部没有冗余的属性
每个函数依赖集F都有最小覆盖,并且不唯一。
最小依赖集的计算:
首先将函数依赖集中的每一个依赖的右部进行分裂,再消除冗余函数依赖和每个函数依赖左部的冗余属性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号