数据库学习摘记 —— 关系代数和关系演算
关系数据结构
笛卡儿积:给定一组集合D1,D2,…,Dn,这些集合可以相同, 定义D1,D2,…,Dn 的笛卡尔积为:D1×D2×…×Dn={(d1,d2,…,dn) | diÎDi,i=l,2,…,n},其中的每一个元素(d1,d2,…,dn)叫做一个n元组,元素中第i个值di叫做第i个分量。
关系:笛卡尔积D1×D2×…×Dn的任一个子集称为 D1,D2,…,Dn 上的一个关系。关系是元组的集合,亦即实 体的集合。
域:集合 D1,D2,…,Dn是关系中元组的取值范围,称为关系的域。关系中的每一列对应一个域,也称为关系的属性,不同的列可以有相同的域,列名对应域名,即属性名。
度:集合 D1,D2,…,Dn的n为关系的度。
候选键:能唯一地标识出一个元组的属性或属性组。
联合键:两个或两个以上属性组成的候选键。
全键:关系的全部属性构成关系的唯一候选键。该关系称为全键关系(All-Key Relation)
主键:在关系的多个候选键中选择的一个候选键,用它作为元组的唯一标示。在一个关系中只能有一个主键。
外键:关系R中的一组属性A不是关系R的主键,但A是另一个关系S的主键,则属性组A就是关系R的外键。
关系模式:若U={A1, A2 …, An}为关系R的属性集,则关系模式简记为R(U)或R(A1, A2, …, An)
完整性规则
实体完整性规则:关系中每个元组的主键属性对应的各个分量不能为空值。
参照完整性规则:设属性组A是关系R的外键且A又是关系S的主键,则对于R中的每一个元组在属性A上的值必须为:空值或者等于S中某一个元组的主键值。
实体完整性和参照完整性都是关系模型必须满足的完整性约束条件,这些约束条件由RDBMS自动支持。
用户定义的完整性:用户根据具体应用而对数据附加的约束条件。
关系代数中传统的集合运算
关系R与S是相容的: 若关系R和S满足:R和S具有相同的度;R中的第i个属性和S中的第i个属性定义在同一个域上。
并运算: R∪S;差运算:R-S;交运算:R∩S
广义笛卡尔积:设R为m元关系,S为n元关 系,则R与S的广义笛卡尔积R×S是一个(m+n) 元关系,其中的每个元组的前m个分量是R中的一个元组,后n个分量是S中的一个元组。若R有k1个元组,S有k2个元组,则R×S有(k1×k2)个元组,即广义笛卡尔积。
关系代数中专门的集合运算
选择运算:从关系Students中选取所有的男生,其关系运算表达式为:σSsex='男'(Students)
投影运算:选取学生关系Sudents中的所有Sname(姓名),Sage(年龄)和Class(班级),其关系运算表达式为:∏Sname, Sage, Class(Students)
连接运算:θ为算术比较符,从二个关系的广义笛卡尔 积中选取满足一定连接条件的元组。

自然连接:两个关系进行连接比较的属性列完全相同的等值连接,且结果关系中没有重复的属性,R 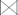 S=ΠB(σR.A=S.A(R×S)),B=ARUAS
S=ΠB(σR.A=S.A(R×S)),B=ARUAS
除法运算:
T=Π1,2,…,n-m(R)
W=(T×S)-R (计算T×S中不在R中的元组)
V=Π1,2,…,n-m(W)
R÷S=T-V
【查询选修了'英语' 课程的学生姓名】

【检索选修了所有课程的学生编号和姓名】
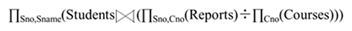
SELECT Sname,Sno
FROM Students WHERE NOT EXISTS
(SELECT * FROM Courses WHERE NOT EXISTS
(SELECT * FROM Reports WHERE
SNO=Students.Sno AND Cno=Course.Cno))
元组关系演算
表达式的一般形式为{ t | α(t)},它是使α(t)为真的所有元组t构成的集合。其中,t是元组变量,α(t)是元组关系演算公式(简称公式),它由原子公式和运算符组成。
S-学生表、R-成绩表、C-课程表
【检索班级编号为'199902'的全班学生的学号】
{t[1] | S(t)∧t[5]='199902'}
【查询选修了'英语' 课程的学生姓名】
{t[2] | S(t)∧ヨu(R(u)∧u[1]= t[1]∧ヨv(C(v)∧v[1]=u[2]∧v[2]='英语'))}
{t[2] | S(t)∧ヨuヨv (R(u)∧C(v)∧u[1]= t[1]∧v[1]=u[2]∧v[2]='英语')}
【检索选修了所有课程的学生】
{t | S(t)∧∀v(C(v)∧ヨu(R(u)∧u[2]=v[1]∧u[1]=t[1]))}
域关系演算
【检索班级编号为'199902'的全班学生的学号】
{t1 | S(t1, t2, t3, t4, t5)∧t5='199902'}}
【查询选修了'英语'课程的学生名】
{t2 | S(t1, t2, t3, t4, t5)∧ヨu1ヨu2ヨv1ヨv2(R(u1, u2, u3)∧C(v1, v2,v3)∧t1=u1∧u2=v1∧v2='英语')}
【检索选修了所有课的学生】
{(t1, t2, t3, t4, t5) | S(t1, t2, t3, t4, t5)∧ヨv1ヨu1ヨu2(R(u1, u2, u3)∧C(v1, v2, v3)∧u2=v1∧u1=t1)}
关系运算的安全限制
无限关系:当元组变元t中某一属性的定义域是无限时,如表示所有不在关系R中的元组的集合{t | ┐R(t)}。
无穷验证过程:t的取值范围为无限,如验证(∀t)(ω(t))为真的过程。
安全表达式:不产生无限关系和无穷验证过程的表达式。
安全限制:为保证所有表达式都是安全表达式所采取的限制措施。
关系代数运算是安全的:当给定的所有关系是有限时,其运算的有限次复合不会出现无限关系和无穷验证。
等价:关系代数、安全的元组关系演算和安全的域关系演算的表达能力是等价的,可以相互转换。
安全限制方法:
定义一个ψ的有限符号集合,记作DOM(ψ)(不必是最小集合),它由以下两类符号构成:
ψ中的常量符号;
ψ中涉及的所有关系的所有元组的各个分量值。
这样,把{t | ┐R(t)}和(∀t)(ω(t))中的t都全部限制在DOM(ψ)中取值,就不会出现无限关系和无穷验证过程,这时关系演算是安全的。
【关系R如右,求元组演算表达式S={t | ┐R(t)}】
令DOM(ψ)=∏A(R)∪∏B(R)∪∏C(R)={a, b, 1, 3, 7, 8},则结果关系:
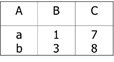
S={ t | ┐R(t)}=DOM(ψ)×DOM(ψ)×DOM(ψ)-R。因此,由于有DOM(ψ)的安全限制,关系S中有216-2=214 个元组,故是有限的。
查询优化
途径:
代数优化:对查询语句进行变换,只改变其基本操作顺序提高查询效率,但不涉及存取路径。
物理优化:根据系统提供的存取路径,比如顺序或索引等来选取较好查询方案。
规则优化:根据一些启发式规则,如先做选择、投影,再做连接操作等来选择较好的查询方案。
代价优化:在规则基础上,对所提供的查询方案进行执行代价估算,选择代价最小的查询方案。
执行代价:
在集中式数据库中,查询的执行代价为:总代价=I/O代价+CPU代价
在多用户环境下查询的执行代价为:总代价=I/O代价+CPU代价+内存代价
查询优化策略(启发式规则):
选择运算应尽早执行
把投影运算和选择运算同时进行
把投影操作与它前面或后面的一个双目运算结合起来
在执行连接运算之前,可对需要连接的关系进行适当地预处理,如建索引或排序
把笛卡尔乘积和其后的选择运算合并成为连接运算
存储公用子表达式
查询优化的等价公式:
- 笛卡儿积、自然连接和条件连接都满足交换律和结合律
- 投影运算的串接:
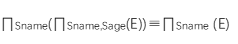
- 选择运算的串接:
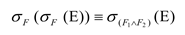
- 选择运算与投影运算交换:
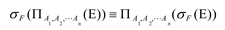
- 选择运算与笛卡尔积交换:
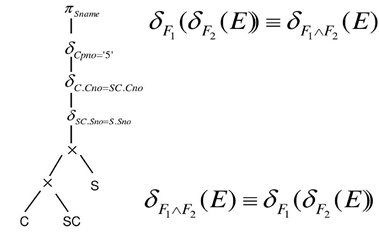
设F中涉及的属性都是E1的属性:

如果F=F1∧F2,且F1只涉及E1的属性,F2只涉及E2的属性: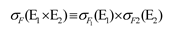
如果F= F1∧F2 ,且F1只涉及E1的属性,F2涉及E1和E2两者的属性: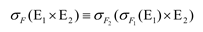
投影运算与笛卡尔积交换:
设E1、E2是两个关系代数表达式,A1,A2,…,An是E1的属性,B1,B2,…,Bm是E2的属性
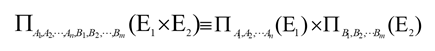
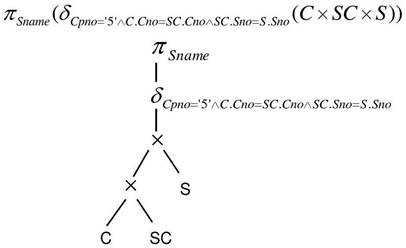
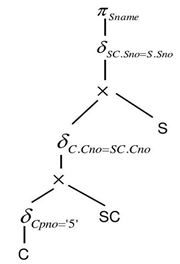
查询优化的步骤:
- 把查询要求转换成某种内部表示 ;
如关系代数语法树;
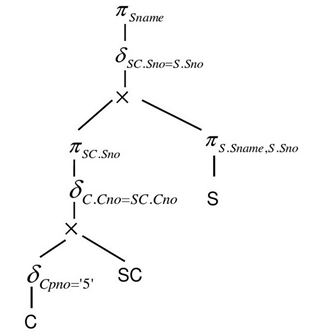
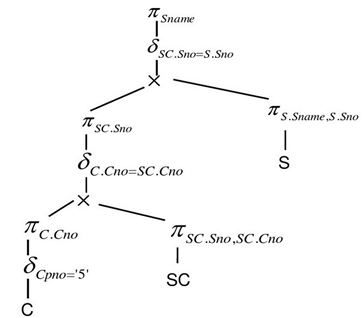
- 把语法树转换成某种优化形式;
利用关系代数等价公式的优化算法
- 选择低层的存取路径;
查询优化器根据数据字典获得当前数据库
- 状态的信息
生成多个查询计划,选择代价最小的去完成查询任务。
【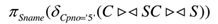 】
】





 浙公网安备 33010602011771号
浙公网安备 33010602011771号