奇偶校验 汉明码 如果一条信息中包含更多用于纠错的位，且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果，那么我们就可以找出出错位了。 crc CRC 循环冗余校验

 

CRC（循环冗余校验）_百度百科 https://baike.baidu.com/item/CRC/1453359

循环冗余校验（Cyclic Redundancy Check， CRC）是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种信道编码技术，主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。

中文名

循环冗余校验

外文名

Cyclic Redundancy Check

简    称

CRC

原    理

除法及余数的原理来作错误侦测

目    的

确保传输的数据准确无误

有关术语

循环冗余校验码

 

 

在数据传输过程中，无论传输系统的设计再怎么完美，差错总会存在，这种差错可能会导致在链路上传输的一个或者多个帧被破坏(出现比特差错，0变为1，或者1变为0)，从而接受方接收到错误的数据。为尽量提高接受方收到数据的正确率，在接收方接收数据之前需要对数据进行差错检测，当且仅当检测的结果为正确时接收方才真正收下数据。检测的方式有多种，常见的有奇偶校验、因特网校验和循环冗余校验等。循环冗余校验是一种用于校验通信链路上数字传输准确性的计算方法（通过某种数学运算来建立数据位和校验位的约定关系的 [1]  ）。发送方计算机使用某公式计算出被传送数据所含信息的一个值，并将此值 附在被传送数据后，接收方计算机则对同一数据进行 相同的计算，应该得到相同的结果。如果这两个 CRC结果不一致，则说明发送中出现了差错，接收方计算机可要求发送方计算机重新发送该数据。

在计算机网络通信中运用CRC校验时相对于其他校验方法就有一定的优势。CRC可以高比例的纠正信息传输过程中的错误，可以在极短的时间内完成数据校验码的计算，并迅速完成纠错过程，通过数据包自动重发的方式使得计算机的通信速度大幅提高，对通信效率和安全提供了保障。由于 CRC 算法检验的检错能力极强，且检测成本较低，因此在对于编码器和电路的检测中使用较为广泛。从检错的正确率与速度、成本等方面，都比奇偶校验等校验方式具有优势。因而，CRC 成为计算机信息通信领域最为普遍的校验方式。

 

在数据存储和数据通讯领域，为了保证数据的正确，就不得不采用检错的手段。在诸多检错手段中，CRC是最著名的一种。CRC的全称是循环冗余校验，其特点是：检错能力强，开销小，易于用编码器及检测电路实现。从其检错能力来看，它所不能发现的错误的几率仅为0.0047%以下。从性能上和开销上考虑，均远远优于奇偶校验及算术和校验等方式。因而，在数据存储和数据通讯领域，CRC无处不在：著名的通讯协议X.25的FCS(帧检错序列)采用的是CRC-CCITT，WinRAR、NERO、ARJ、LHA等压缩工具软件采用的是CRC32，磁盘驱动器的读写采用了CRC16，通用的图像存储格式GIF、TIFF等也都用CRC作为检错手段。下面介绍硬件生成与计算CRC的过程。

 

 

下面以最常用的CRC-16为例来说明其生成过程。

CRC-16码由两个字节构成，在开始时CRC寄存器的每一位都预置为1，然后把CRC寄存器与8-bit的数据进行异或，之后对CRC寄存器从高到低进行移位，在最高位（MSB）的位置补零，而最低位（LSB，移位后已经被移出CRC寄存器）如果为1，则把寄存器与预定义的多项式码进行异或，否则如果LSB为零，则无需进行异或。重复上述的由高至低的移位8次，第一个8-bit数据处理完毕，用此时CRC寄存器的值与下一个8-bit数据异或并进行如前一个数据似的8次移位。所有的字符处理完成后CRC寄存器内的值即为最终的CRC值。

1．设置CRC寄存器，并给其赋值FFFF(hex)。

2．将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或，并把结果存入CRC寄存器。

3．CRC寄存器向右移一位，MSB补零，移出并检查LSB。

4．如果LSB为0，重复第三步；若LSB为1，CRC寄存器与多项式码相异或。

注意：该步检查LSB应该是右移前的LSB，即第3步前的LSB。

5．重复第3与第4步直到8次移位全部完成。此时一个8-bit数据处理完毕。

6．重复第2至第5步直到所有数据全部处理完成。

7．最终CRC寄存器的内容即为CRC值。

 

 

 

  CRC（循环冗余校验）在线计算_ip33.com http://www.ip33.com/crc.html

 

 

zlib Home Site https://www.zlib.net/

zlib 1.2.11 Manual https://www.zlib.net/manual.html

 rfc1952 https://datatracker.ietf.org/doc/html/rfc1952

 

 

parity bit
奇偶位 校验位

n 有效信息的位数
k 校验位的位数

2^k-1>=n+k
k=4 => n(Max)=11
n=4 => k(Min)=3

 

 

If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.

偶校验

 

 

 

海明码之编码原理和校验方法_夜风的博客-CSDN博客_海明码 https://blog.csdn.net/u014470361/article/details/79848824

 

 

The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. 

General algorithm[edit]

The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.

An algorithm can be deduced from the following description:

1. Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
2. Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
3. All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
4. All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
5. Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
   1. Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
   2. Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
   3. Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
   4. Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
   5. In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.

If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.

The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.

This general rule can be shown visually:

 

 Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.

 

 

 

 

 

 

 

 

https://en.wikipedia.org/wiki/Block_code#The_block_length_n

https://zh.wikipedia.org/wiki/分組碼

分组码（block code），又名块码，是信道编码（channel coding）技术的一种。它在传送端发送的原始讯息中，以比特率不会超过信道容量为前提下，加入额外的比特（redundancy），使接收端能够以最小（理论值为0）的错误率解码。

分组码主要的特性为它的密码长度固定（有别于使用变长编码表的霍夫曼编码（Huffman Coding））。一般来说分组码会将包含了k位数的信息字符s，转换到包含n位数的编码字符C(s)；即分组码长度（block length）为n。

分组编码是早期移动通信（mobile communication）系统中，使用的主要信道编码（channel coding）方式。

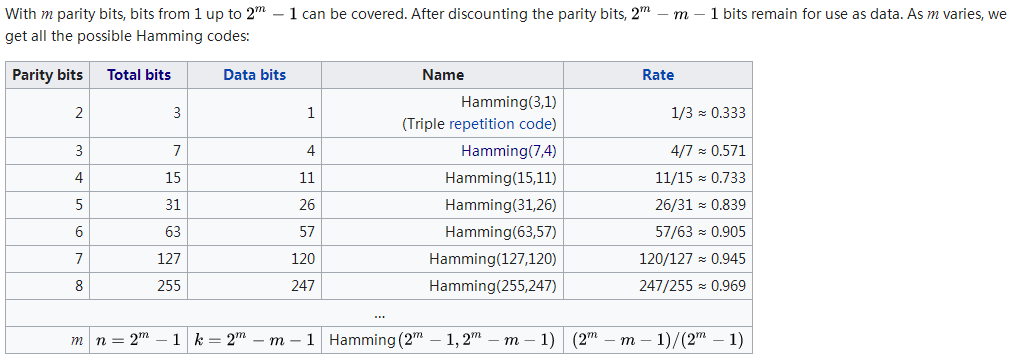
Block code - Wikipedia https://en.wikipedia.org/wiki/Block_code#The_block_length_n

In coding theory, block codes are a large and important family of error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of all block codes in a unified way. Such limitations often take the form of bounds that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors.

 

 

 

 

 

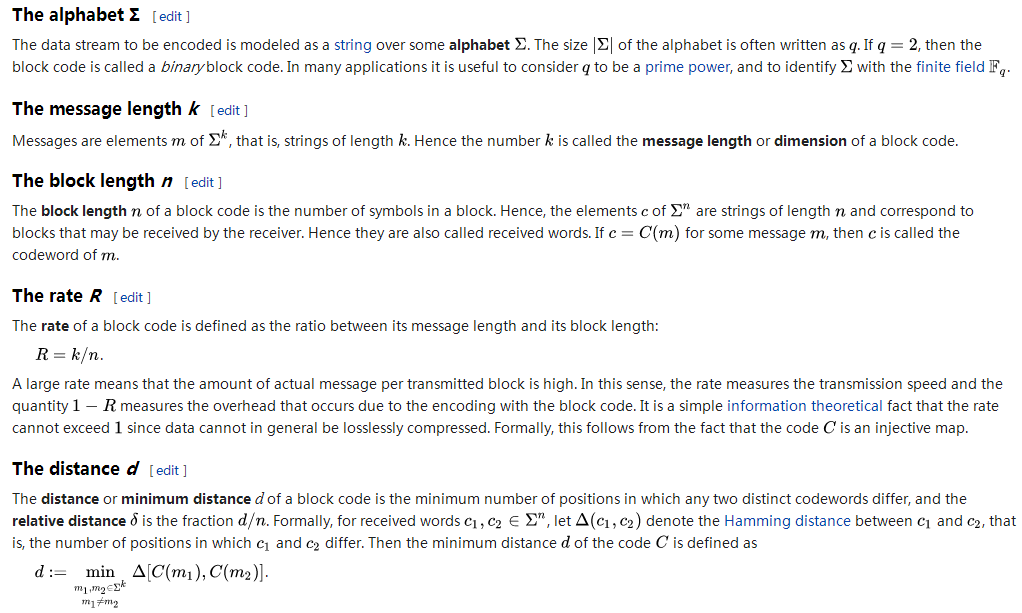
The message length k
The block length n
The rate R
The distance d

 

 

 

Hamming code - Wikipedia https://en.wikipedia.org/wiki/Hamming_code

 

st=>start: 开始
e=>end: 结束
ipt=>inputoutput: 输入一个x
op=>operation: 第i个检验位的第1个的检验位是第2^i-1位，从该位开始
cond1=>condition: 至少有(2^i-1)*2位
sub1=>subroutine: 先一共检验2^i-1位
sub2=>subroutine: 再一共跳过2^i-1位
st->ipt->op->cond1->sub1->sub2->cond1
sub2->cond1
cond1(yes,left)->sub1
cond1(no)->e

 

 

 

 

 

 

https://zh.wikipedia.org/wiki/汉明距离

在信息论中，两个等长字符串之间的汉明距离（英语：Hamming distance）是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。

汉明重量是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是1的个数，所以11101的汉明重量是4。

范例

例如：

• 1011101与1001001之间的汉明距离是2。
• 2143896与2233796之间的汉明距离是3。
• "toned"与"roses"之间的汉明距离是3。

特性

对于固定的长度n，汉明距离是该长度字符向量空间上的度量，很显然它满足非负、唯一及对称性，并且可以很容易地通过完全归纳法证明它满足三角不等式。

两个字a与b之间的汉明距离也可以看作是特定运算−的a−b的汉明重量。

对于二进制字符串a与b来说，它等于a 异或b以后所得二进制字符串中“1”的个数。另外二进制字符串的汉明距离也等于n维超正方体两个顶点之间的曼哈顿距离，其中n是两个字串的长度。

历史及应用

汉明距离是以理查德·卫斯里·汉明的名字命名的，汉明在误差检测与校正码的基础性论文中首次引入这个概念。在通信中累计定长二进制字中发生翻转的错误数据位，所以它也被称为信号距离。汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

 

 

 

 

汉明码 - 维基百科，自由的百科全书 https://zh.wikipedia.org/zh-cn/汉明码

notes1.pdf http://www.cs.cmu.edu/~venkatg/teaching/codingtheory/notes/notes1.pdf

例子

对11000010进行汉明编码，求编码后的码字。

1.列出表格，从左往右（或从右往左）填入数字，但2的次方的位置不填。

位置	1	2	3	4	5	6	7	8	9	10	11	12
数据			1		1	0	0		0	0	1	0

2.把数据行有1的列的位置写为二进制。

位置	1	2	3	4	5	6	7	8	9	10	11	12
数据			1		1	0	0		0	0	1	0
二进制			0011		0101						1011

3.收集所有二进制数字，求异或。

4.把1101依次填入表格中2的次方的位置（低位在左）。

位置	1	2	3	4	5	6	7	8	9	10	11	12
数据			1		1	0	0		0	0	1	0
二进制			0011		0101						1011
校验	1	0		1				1

5.所以编码后的码字是101110010010。

 

 

 原始数据和奇偶位组成的新数据中，将总共包含偶数个1. 奇偶校验并不总是有效，如果数据中有偶数个位发生变化，则奇偶位仍将是正确的，因此不能检测出错误。

 

在一个7位的信息中，单个位出错有7种可能，因此3个错误控制位就足以确定是否出错及哪一位出错了。

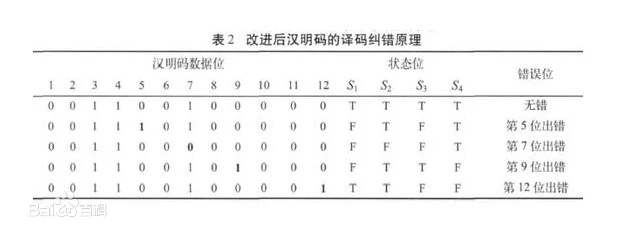
 所有校验位覆盖了数据位置和该校验位位置的二进制与的值不为0的数。

 

 

  

 

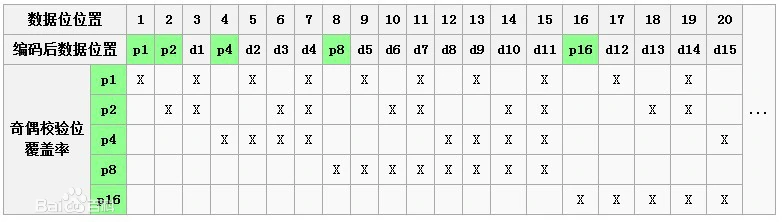
奇偶校验位 汉明码 如果一条信息中包含更多用于纠错的位，且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果，那么我们就可以找出出错位了。

奇偶校验位 汉明码

 

奇偶校验位_百度百科 https://baike.baidu.com/item/奇偶校验位
汉明码_百度百科 https://baike.baidu.com/item/汉明码/3226749

 

汉明码（Hamming Code），是在电信领域的一种线性调试码，以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码，当计算机存储或移动数据时，可能会产生数据位错误，以侦测并更正单一比特错误。由于汉明编码简单，它们被广泛应用于内存（RAM）。

 

 

中文名

汉明码

外文名

Hamming Code

目录

1. 1 历史
2. 2 校验

1. 3 纠错
2. 4 校验方法

1. 5 编码原理
2. 6 数量之比

历史

 语音

人们在汉明码出现之前使用过多种检查错误的编码方式，但是没有一个可以在和汉明码在相同空间消耗的情况下，得到相等的效果。

1940年，汉明于贝尔实验室（Bell Labs）工作，运用贝尔模型V（Bell Model V）电脑，一个周期时间在几秒钟内的机电继电器机器。输入端是依靠打孔卡（Punched Card），这不免有些读取错误。在平日，特殊代码将发现错误并闪灯（flash lights），使得操作者能够纠正这个错误。在周末和下班期间，在没有操作者的情况下，机器只会简单地转移到下一个工作。汉明在周末工作，他对于不可靠的读卡机发生错误后，总是必须重新开始项目变得愈来愈沮丧。在接下来的几年中，他为了解决调试的问题，开发了功能日益强大的调试算法。在1950年，他发表了今日所称的汉明码。现在汉明码有着广泛的应用。

校验

 语音

与其他的错误校验码类似，汉明码也利用了奇偶校验位的概念，通过在数据位后面增加一些比特，可以验证数据的有效性。利用一个以上的校验位，汉明码不仅可以验证数据是否有效，还能在数据出错的情况下指明错误位置。

纠错

 语音

在接收端通过纠错译码自动纠正传输中的差错来实现码纠错功能，称为前向纠错FEC。在数据链路中存在大量噪音时，FEC可以增加数据吞吐量。通过在传输码列中加入冗余位(也称纠错位)可以实现前向纠错。但这种方法比简单重传协议的成本要高。汉明码利用奇偶块机制降低了前向纠错的成本。

校验方法

 语音

如果一条信息中包含更多用于纠错的位，且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果，那么我们就可以找出出错位了。在一个7位的信息中，单个位出错有7种可能，因此3个错误控制位就足以确定是否出错及哪一位出错了。

汉明码SECDED（single error correction, double error detection）版本另外加入一检测比特，可以侦测两个或以下同时发生的比特错误，并能够更正单一比特的错误。因此，当发送端与接收端的比特样式的汉明距离（Hamming distance）小于或等于1时（仅有1 bit发生错误），可实现可靠的通信。相对的，简单的奇偶检验码除了不能纠正错误之外，也只能侦测出奇数个的错误。

下列通用算法可以为任意位数字产生一个可以纠错一位的汉明码：

1.从1开始给数字的数据位（从左向右）标上序号, 1，2，3，4，5...

2.将这些数据位的位置序号转换为二进制，1, 10, 11, 100, 101,等。

3.数据位的位置序号中所有为二的幂次方的位（编号1，2，4，8，等，即数据位位置序号的二进制表示中只有一个1）是校验位

4.所有其它位置的数据位（数据位位置序号的二进制表示中至少2个是1）是数据位

5.每一位的数据包含在特定的两个或两个以上的校验位中，这些校验位取决于这些数据位的位置数值的二进制表示

(1) 校验位1覆盖了所有数据位位置序号的二进制表示倒数第一位是1的数据：1（校验位自身，这里都是二进制，下同），11，101，111，1001，等

(2) 校验位2覆盖了所有数据位位置序号的二进制表示倒数第二位是1的数据：10（校验位自身），11，110，111，1010，1011，等

(3) 校验位4覆盖了所有数据位位置序号的二进制表示倒数第三位是1的数据：100（校验位自身），101，110，111，1100，1101，1110，1111，等

(4) 校验位8覆盖了所有数据位位置序号的二进制表示倒数第四位是1的数据：1000（校验位自身），1001，1010，1011，1100，1101，1110，1111，等

(5) 简而言之，所有校验位覆盖了数据位置和该校验位位置的二进制与的值不为0的数。

采用奇校验还是偶校验都是可行的。偶校验从数学的角度看更简单一些，但在实践中并没有区别。校验位一般的规律可以如下表示：

观察上表可发现一个比较直观的规律：第i个检验位是第2^(i-1)位，从该位开始，检验2^(i-1)位，跳过2^(i-1)位……依次类推。例如上表中第3个检验位p4从第23-1=4位开始，检验4、5、6、7共4位，然后跳过8、9、10、11共4位，再检验12、13、14、15共4位…… [1] 

编码原理

 语音

奇偶校验是一种添加一个奇偶位用来指示之前的数据中包含有奇数还是偶数个1的检验方式。如果在传输的过程中，有奇数个位发生了改变，那么这个错误将被检测出来（注意奇偶位本身也可能改变）。一般来说，如果数据中包含有奇数个1的话，则将奇偶位设定为1；反之，如果数据中有偶数个1的话，则将奇偶位设定为0。换句话说，原始数据和奇偶位组成的新数据中，将总共包含偶数个1. 奇偶校验并不总是有效，如果数据中有偶数个位发生变化，则奇偶位仍将是正确的，因此不能检测出错误。而且，即使奇偶校验检测出了错误，它也不能指出哪一位出现了错误，从而难以进行更正。数据必须整体丢弃并且重新传输。在一个噪音较大的媒介中，成功传输数据可能需要很长时间甚至不可能完成。虽然奇偶校验的效果不佳，但是由于他只需要一位额外的空间开销，因此这是开销最小的检测方式。并且，如果知道了发生错误的位，奇偶校验还可以恢复数据。 如果一条信息中包含更多用于纠错的位，且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果，那么我们就可以找出出错位了。在一个7位的信息中，单个数据位出错有7种可能，因此3个错误控制位就足以确定是否出错及哪一位出错了。 [2] 

一般来说，若汉明码长为n，信息位数为k，则监督位数r=n-k。若希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能位置，则要求

2^r-1≥n或2^r≥k+r+1 [3] 

现以数据码1101为例说明汉明码编码原理，此时D4=1、D3=1、D2=0、D1=1，在P1编码时，先将D4、D3、D1的二进制码相加，结果为奇数3，汉明码对奇数结果编码为1，偶数结果为0（奇数位。若奇数结果编码为0.偶数结果为1，则叫偶数位），因此P1值为1，D4+D2+D1=2，为偶数，那么P2值为0，D3+D2+D1=2，为偶数，P3值为0。这样，参照上文的位置表，汉明码处理的结果就是1101001。在这个4位数据码的例子中，我们可以发现每个汉明码都是以三个数据码为基准进行编码的。下面就是它们的对应表：

汉明码	编码用的数据码
P1	D8、D4、D1
P2	D8、D2、D1
P3	D4、D2、D1

从编码形式上，我们可以发现汉明码是一个校验很严谨的编码方式。在这个例子中，通过对4个数据位的3个位的3次组合检测来达到具体码位的校验与修正目的（不过只允许一个位出错，两个出错就无法检查出来了，这从下面的纠错例子中就能体现出来）。在校验时则把每个汉明码与各自对应的数据位值相加，如果结果为偶数（纠错代码为0）就是正确，如果为奇数（纠错代码为1）则说明当前汉明码所对应的三个数据位中有错误，此时再通过其他两个汉明码各自的运算来确定具体是哪个位出了问题。

还是刚才的1101的例子，正确的编码应该是1101001，对应D4 D3 D2 D1 P3 P2 P1。如果第三个数据位在传输途中因干扰而变成了1，就成了1111001, 即 D2=1。检测时，P1=D4+D3+D1=1+1+1的结果是奇数3，除以2余数1，原来第一位纠错代码为1，正确。P2=D3+D2+D1的结果是奇数3，除以2余数1，而原来第二位纠错代码为0，有错误。P3=D3+D2+D1的结果是奇数3，除以2余数1，而原来第三位纠错代码为0，有错误。可推断是第2位出现错误。 [4] 

数量之比

 语音

那么汉明码的数量与数据位的数量之间有何比例呢？上面的例子中数据位是4位，加上3位汉明码是7位，而2的3次幂是8。这其中就存在一个规律，即2^P≥P+D+1，其中P代表汉明码的个数，D代表数据位的个数，比如4位数据，加上1就是5，而能大于5的2的幂数就是3（2^3=8，2^2=4）。这样，我们就能算出任何数据位时所需要的汉明码位数：7位数据时需要4位汉明码（16>4+7+1），64位数据时就需要7位汉明码（128>64+7+1），大家可以依此推算。此时，它们的编码规也与4位时不一样了。