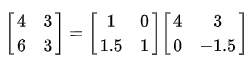LU decomposition can be viewed as the matrix form of Gaussian elimination.
https://en.wikipedia.org/wiki/LU_decomposition
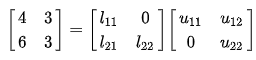
One way to find the LU decomposition of this simple matrix would be to simply solve the linear equations by inspection. Expanding the matrix multiplication gives
This system of equations is underdetermined. In this case any two non-zero elements of L and U matrices are parameters of the solution and can be set arbitrarily to any non-zero value. Therefore, to find the unique LU decomposition, it is necessary to put some restriction on L and U matrices. For example, we can conveniently require the lower triangular matrix L to be a unit triangular matrix (i.e. set all the entries of its main diagonal to ones). Then the system of equations has the following solution: