置换群
被ZJOI 2018 DAY2 T1 逼得滚回去学数学了。(⊙o⊙)…
学了一些置换群的理论。
有一些定义：
群：符合结合律，单位元，逆元的东西。
abel群： 符合交换律的群
群的阶： 群中集合的元素个数；
生成子群： 拿出一些元素后互相生成所产生的群。
陪集： 拿一个元素出来，左乘或右乘一个子群所产生的群。
定理1.设H是群G的子群，对任意H的两个左陪集aH和bH，要么aH=bH,要么aH∩bH=∅，对右陪集亦然；
等价于随便找一个G的子群H，H的不相等的（左|右）陪集们不重不漏地包含了G的所有元素；
一个符号：记|G:H|表示G中H的不同右的个数，如，设1为G的子群，且只包含单位元，则|G:1|=|G|，即集合G的大小，也即群G的阶；
那么有 |G:H|=|G|/|H|
定理2:若H是G的子群，则|G:x|=|G:H||H:x|
定理3:设H是有限群 
的子群，则
的阶整除
的阶。
置换： 一个有限集X的置换π是从该有限集映至自身的双射；如果我们把G的元素从1到|X|编号，那么置换π可以看做一个1到|X|的一个排列；实在不行就理解成行列式中那个决定前面系数的那个东西
由目测可知，置换成abel 群。
轨道与等价类：
原数列集合中的元素β，在置换群G中的所有置换中的像，构成的集合叫做β的轨道，记作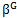
,我们也称其为包括β的等价类；
稳定子群（集）与稳定化子：
有限集X中某m个元素构成了X的一个子集A，置换群G中可以使A中所有元素不动的置换构成的子群叫做A的一个稳定子群，又称稳定集，记为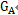
；
该定义在m=1时，需要特别关注，也就是有限集X中的元素k，置换群G中可以使元素k不动的置换构成的子群（对其他元素不做要求），记为Gk，我们也称其为k的稳定化子；通俗的讲，就是不动点所成的群。
轨道-稳定集定理：
|kG|*|Gk|=|G|;
证明：由定理1 ，2 可知是充分的划分。
又因为置换等于一系列轮换的积，在加上行列式的第二定义，易得上述结论。⊙o⊙…
Burnside引理:
轨道数=不动点数之和/置换群的阶
由轨道-稳定集定理易得。
Polya定理
就是把burnside引理写成轮换形式。
poj 2369
给你一个排列p，求k，使得p^k=p
先找出所有的轮换，然后循环阶数的lcm就是答案了
poj 1026
给你一个长度为n的置换，然后给你m是下面做置换的次数，再给你个字符串，长度为n，空的地方用空格，然后求置换后的字符串
找轮换后暴力。
poj 1721
给一个置换p |p|<=1000,求 log 2 p
由群的性质得这个操作会循环，那么暴力。
CodeForces 612E
给一个置换p |p|<=1000000,求 sqrt p
奇偶讨论
poj 3270
给你一个排列，然后让你交换到递增排列，交换X和Y的位置，花费就是X+Y，求变成递增序列的最小花费
贪心
未完待续。。。
