SPLAY 模板

经典引文

空间效率：O(n)

时间效率：O(log n)插入、查找、删除

创造者：Daniel Sleator 和 Robert Tarjan

优点：每次查询会调整树的结构，使被查询频率高的条目更靠近树根。

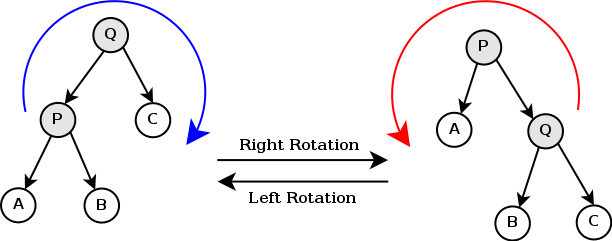
Tree Rotation

 

树的旋转是splay的基础，对于二叉查找树来说，树的旋转不破坏查找树的结构。

 

Splaying

 

Splaying是Splay Tree中的基本操作，为了让被查询的条目更接近树根，Splay Tree使用了树的旋转操作，同时保证二叉排序树的性质不变。

Splaying的操作受以下三种因素影响：

• 节点x是父节点p的左孩子还是右孩子
• 节点p是不是根节点，如果不是
• 节点p是父节点g的左孩子还是右孩子

同时有三种基本操作：

Zig Step

当p为根节点时，进行zip step操作。

当x是p的左孩子时，对x右旋；

当x是p的右孩子时，对x左旋。

 

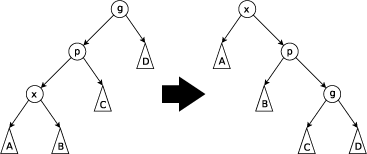
Zig-Zig Step

当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。

当x和p同为左孩子时，依次将p和x右旋；

当x和p同为右孩子时，依次将p和x左旋。

 

 

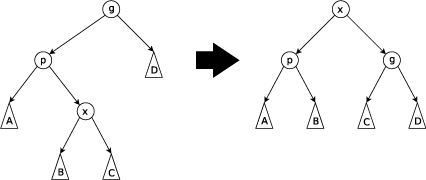
Zig-Zag Step

当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。

当p为左孩子，x为右孩子时，将x左旋后再右旋。

当p为右孩子，x为左孩子时，将x右旋后再左旋。

总结：

    rotate操作的核心是把点和其父亲换位置，然后维护中序就好了。

   我们可以通过复杂度分析发现是log级的。

文艺平衡树：

#pragma GCC optimize("-O2")
#include<bits/stdc++.h>
#define N 100005
using namespace std;
int f[N],ch[N][2],siz[N],rev[N],rt;
#define Mid (l+r>>1)
#define sight(x) ('0'<=x&&x<='9')
inline void read(int &x){
    static char c;
    for (c=getchar();!sight(c);c=getchar());
    for (x=0;sight(c);c=getchar())x=x*10+c-48;
}
void write(int x){if (x<10) {putchar('0'+x); return;} write(x/10); putchar('0'+x%10);}
inline void writeln(int x){ if (x<0) putchar('-'),x*=-1; write(x); putchar('\n'); }
inline void writel(int x){ if (x<0) putchar('-'),x*=-1; write(x); putchar(' '); }
inline void pb(int x){
    siz[x]=1+siz[ch[x][0]]+siz[ch[x][1]];
}
inline void pd(int x){
    if (!rev[x]) return ;
    swap(ch[x][0],ch[x][1]);
    rev[ch[x][0]]^=1,rev[ch[x][1]]^=1; rev[x]=0;
}
int build(int l,int r,int fa){
    if (l>r) return 0; f[Mid]=fa;
    ch[Mid][0]=build(l,Mid-1,Mid);
    ch[Mid][1]=build(Mid+1,r,Mid);
    pb(Mid); return Mid;
}
int x,y,z,kind;
void rotate(int x,int &k) {
    int y=f[x],z=f[y],kind=(ch[y][0]==x);
    if (y==k) k=x;else {ch[z][ch[z][0]!=y]=x;}
       ch[y][kind^1]=ch[x][kind]; f[ch[y][kind^1]]=y;
       ch[x][kind]=y; f[y]=x; f[x]=z;
       pb(x); pb(y);
}
void splay(int x,int &k){
    while (x^k) {
        int y=f[x],z=f[y];
        if (y^k) {
            if ((ch[y][0]==x)^(ch[z][0]==y)) rotate(x,k); 
            else rotate(y,k);
        }
        rotate(x,k);
    }
}
int s,n,m,l,r;
int find(int x,int k) {
    pd(x); s=siz[ch[x][0]];
    if (k==s+1) return x;
    if (k<=s) return find(ch[x][0],k);
    else return find(ch[x][1],k-s-1);
}
void rever(int l,int r){
    x=find(rt,l); y=find(rt,r+2);
    splay(x,rt); splay(y,ch[x][1]); 
    rev[ch[y][0]]^=1;
}
signed main () {
    freopen("testdata.in","r",stdin);
    read(n); read(m); rt=n+3>>1;
    ch[rt][0]=build(1,rt-1,rt);
    ch[rt][1]=build(rt+1,n+2,rt);
    while (m--) {
        read(l); read(r);
        rever(l,r);
    }
    for (int i=2;i<=n+1;i++) writel(find(rt,i)-1);
}