ACM-东北赛划水记

今天东北赛，滑了一天水，做了几道题。

T8：

1. 题意：字符串压缩

 

 

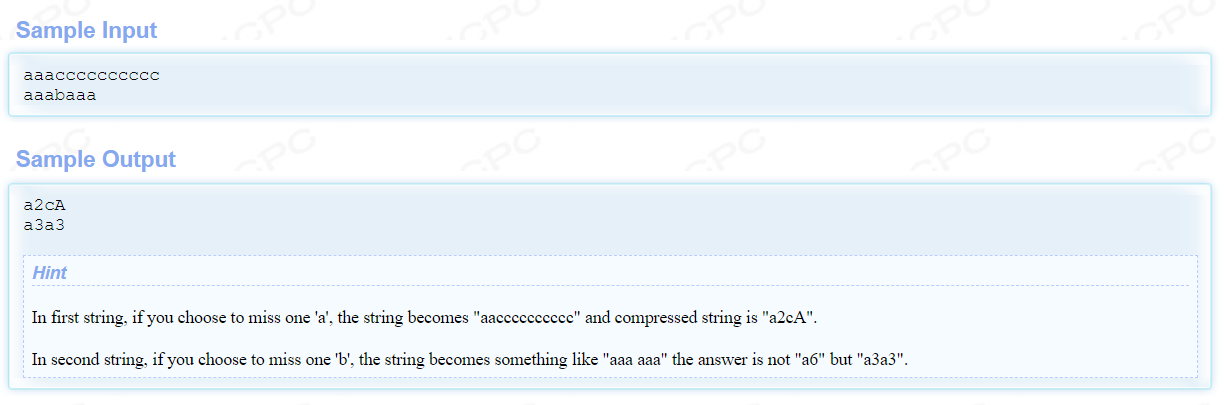
SOL：优先压缩长度，再选字典序最优。注意可能对长度有贡献的数字1 2 16  16*16 16*16*16......

          把这些点记录下来，再对每个点进行尝试，判断去掉一个字符后对字典序的贡献是减少还是增加，如果有减少的点，选减少的最前面的那个点，不然就选增加的最后一个点。

#include<bits/stdc++.h>
#define N 1000007
using namespace std;
int t[17],len,tag,c[N],ta[N],sb,sb1,sb2,ff1[N],ff2[N];
char p[N],s[N];
bool get_ab() {
    for (int i=1;i<=tag;i++) {
        for (int j=1;j<=6;j++) 
            if (c[i]==t[j]) {ta[++sb]=i; break;}
    }
    return sb!=0;
}
void out(int x) {
    if (x==0) return;
    out(x/16); x=x%16;
    if (0<=x&&x<10) putchar(48+x); else putchar(55+x);
}
signed main () {
    t[1]=1; t[2]=2; t[3]=16; t[4]=256; 
    t[5]=4096; t[6]=65536; 
    while (scanf("%s",s+1)!=EOF) {
        len=strlen(s+1); tag=0; sb=0;
        for (int i=1;i<=len;i++) {
            if (s[i]==s[i-1]) c[tag]++;
            else p[++tag]=s[i],c[tag]=1;
        }
        if (get_ab()) { sb1=sb2=0;
            for (int i=1;i<=sb;i++) {
             if  (c[ta[i]]==1) {
                 if (p[ta[i]]>p[ta[i]+1]) ff1[++sb1]=ta[i]; else ff2[++sb2]=ta[i];}
             if (c[ta[i]]==2) { ff2[++sb2]=ta[i];}
             if (c[ta[i]]>2) { ff2[++sb2]=ta[i];}
             }
            if (sb1!=0) c[ff1[1]]--; else c[ff2[sb2]]--;
        } else {c[1]--;}
        for (int i=1;i<=tag;i++) {
            if (c[i]==0) continue;
            if (c[i]==1) { putchar(p[i]); continue;}
            putchar(p[i]); out(c[i]);
        }
        putchar('\n');
    }
}

T10

 

可以发现，如果n充分大，那么对于y同奇偶的点，选定一个点的颜色，其他都唯一确定了。 所以2个自由元，答案为4

n比较小的时候写暴力观察即可。

#include<bits/stdc++.h>using namespace std;
long long f[73];int T,n,k;
signed main () {
    scanf("%d",&T);
    while (T--) {
        scanf("%d%d",&n,&k);
        if (n==1&&k==1) {puts("1"); continue;}
        if (n==k||k==0) {puts("-1"); continue;}
        if (k%2==1) {
        for (int i=1;i<=k+1;i++) 
          f[i]=(1ll<<k+1)-1ll-(1ll<<(k+1-i));
        for (int i=k+2;i<=n;i++) f[i]=(1ll<<i-1)+(1ll<<k-1)-1ll;
        for (int i=1;i<n;i++) printf("%lld ",f[i]); printf("%lld\n",f[n]); 
        } else {
            puts("-1"); continue;
        }
    }
}

 

T5

咋一看像线性基，其实不是

 

对于k是奇数，可以发现选后k+1位分别选一位为0即可。

对于偶数，认真观察（瞎几把猜）可以发现是无解的（不会证明）

#include<bits/stdc++.h>
using namespace std;
long long f[73];int T,n,k;
signed main () {
    scanf("%d",&T);
    while (T--) {
        scanf("%d%d",&n,&k);
        if (n==1&&k==1) {puts("1"); continue;}
        if (n==k||k==0) {puts("-1"); continue;}
        if (k%2==1) {
        for (int i=1;i<=k+1;i++) 
          f[i]=(1ll<<k+1)-1ll-(1ll<<(k+1-i));
        for (int i=k+2;i<=n;i++) f[i]=(1ll<<i-1)+(1ll<<k-1)-1ll;
        for (int i=1;i<n;i++) printf("%lld ",f[i]); printf("%lld\n",f[n]); 
        } else {
            puts("-1"); continue;
        }
    }
}

T13

 

水题，不多bb

Code Render Status : Rendered By HDOJ G++ Code Render Version 0.01 Beta
#include<bits/stdc++.h>
using namespace std;
int  p[1000007];
void t(int x){
    if (x<1||x>1000000) return;
    p[x]=1;
}
int T,x;
signed main () {
    p[1]=1;
    for (int i=1;i<=1000000;i++) 
     if (p[i]) { 
         t(i*5+13);
         t(i*5-13);
         t(i*13-5);
         t(i*13+5);
     }
    scanf("%d",&T);
    while (T--) {
        scanf("%d",&x);
//        if (x>)
        puts(p[x]?"Yes":"No");
    }
}