【11】三个重要统计量的分布(1)
【11】三个重要统计量的分布(1)
假设检验问题的基础内容,三大抽样分布在多元形态下的推广。
分量独立的 \(n\) 维随机向量\(X\)的二次型
\(\chi^2\)得复习节。。。
设\(X_i\sim N_1(\mu_i,\sigma^2)(i=1,...,n)\),且相互独立,记
则\(X\sim N_n(\mu=(\mu_1,...,\mu_n)',\sigma^2I_n)\).
- 当\(\mu_i=0,(i=1,...,n),\sigma^2=1\)时(每一个都是标准正态):
- 当\(\mu_i=0,\sigma^2\neq1\)时,(凑成标准正态)
- 当\(\color{red}\mu_i\neq0\)时,\(X'X\)的分布称为非中心\(\chi^2\)分布。
(def)
设 \({r.v.}\ X_{n\times1}\sim N_n(\mu,I_n),(\mu\neq0)\),则称 \(\xi=X'X\) 为服从 \(n\) 个自由度,非中心参数 \(\delta=\mu'\mu=\sum_{i=1}^n\mu^2_i\) 的 \(\chi^2\) 分布,记为:
\[X'X\sim\chi^2(n,\delta)\color{gray}or\color{black}\chi^2_{n}(\delta) \]
(推广)
如何将一般的正态随机向量 (协方差矩阵不是单位阵) 转化成服从 \(\chi^2\)分布。
设\(X\sim N_p(\mu,\Sigma>0)\),则\(X'\Sigma^{-1}X\sim\chi^2(p,\delta=\mu'\Sigma^{-1}\mu)\).
由于\(\Sigma\)是正定矩阵,则可以分解为非退化方阵的乘积:\(\Sigma=CC'\),则令 \(Y=C^{-1}X\),于是有:
\[Y\sim N(C^{-1}\mu,C^{-1}\Sigma(C^{-1})') \]因为\(\Sigma=CC'\)所以,\(Y\sim N_p(C^{-1}\mu,I_n)\),且有:
\[X'\Sigma^{-1}X=Y'C'\Sigma^{-1}CY=Y'Y\sim \chi^2(p,\delta) \]其中:
\[\delta=(C^{-1}\mu)'(C^{-1}\mu)=\mu'\Sigma^{-1}\mu \]
- (对称幂等矩阵)
【结论很重要】
设\(X\sim N_n(0_n,\sigma^2I_n)\), \(A\) 为对称矩阵,\(rank(A)=r\) ,则二次型:\(\frac{X'AX}{\sigma^2}\sim\chi^2(r)\Leftrightarrow A^2=A\).
\(\rightrightarrows\)
因为 \(A\) 是对称矩阵,所以存在正交阵 \(\Gamma\) 使得:
\[\Gamma'A\Gamma=diag(\lambda_1,...,\lambda_r,0,...,0) \]令
\[Y=\Gamma'X\sim N_n(0_n,\sigma^2I_n),X=\Gamma Y \]则
\[\xi=X'AX/\sigma^2=Y'\Gamma'A\Gamma Y/\sigma^2=\sum_{i=1}^r\lambda_iY_i^2/\sigma^2 \]且\(Y_1,...,Y_r\)独立同\(N(0,\sigma^2)\)分布,因此,\(Y_i^2/\sigma^2\sim\chi^2(1),(i=1,...,r)\),且相互独立。
\(\sum_{i=1}^r\lambda_iY_i^2/\sigma^2\)的特征函数为:
\[(1-2i\lambda_1t)^{-1/2}(1-2i\lambda_2t)^{-1/2}...(1-2i\lambda_rt)^{-1/2} \]又因为\(\xi=X'AX/\sigma^2\sim\chi^2(r)\),因此他的特征函数为:
\[(1-2it)^{-r/2}=(1-2i\lambda_1t)^{-1/2}(1-2i\lambda_2t)^{-1/2}...(1-2i\lambda_rt)^{-1/2} \]比较得:\(\lambda_1=...=\lambda_r=1\),于是:
\[diag(1,...,1,0,...,0)=\Gamma'A\Gamma=\Gamma'A\Gamma\cdot\Gamma'A\Gamma=\Gamma'A^2\Gamma \]所以\(A\)是对称幂等矩阵。
\(\leftleftarrows\)
对称幂等矩阵的特征值非0即1,且只有r个非0特征值,即:
\[\Gamma'A\Gamma=\left[\begin{array}{cc}I_r&O\\O&O\end{array}\right] \]令\(Y=\Gamma'X\),则 \(Y\sim N_n(0_n,\sigma^2\Gamma'I_n\Gamma)=N_n(0_n,\sigma^2I_n)\).
\[\frac{X'AX}{\sigma^2}=\frac{Y'\Gamma'A\Gamma Y}{\sigma^2}=\frac1{\sigma^2}Y'\left[\begin{array}{cc}I_r&O\\O&O\end{array}\right]Y=\frac1{\sigma^2}\sum_{i=1}^rY_i^2\sim\chi^2(r) \]
- (二次型与线性函数的独立性)
设\(X\sim N_n(\mu,\sigma^2I_n)\),\(A\)为\(n\)阶对称矩阵,\(B\)为\(m\times n\)矩阵,令 \(\xi=X'AX,Z_{m\times1}=BX\) ,若 \(BA=O\) , 则\(BX,X'AX\) 相互独立。
顺序不能换。
- (两个二次型相互独立)
设\(X\sim N_n(\mu,\sigma^2I_n)\) , \(A,B\) 为 \(n\) 阶对称矩阵,则:
\(\chi^2\to Wishart\)分布
设\(X_{(\alpha)}\sim N_p(0,\Sigma),(\alpha=1,...,n)\)相互独立,记\(X=(X_{(1)},...,X_{(n)})'\)为\(n\times p\)维矩阵,则称
的分布为\(\color{red}Wishart\)分布,记为:\(W\sim W_p(n,\Sigma)\).
- 当\(p=1\)时,\(X_{(\alpha)}\sim N_1(0,\sigma^2),W=\sum X_{(\alpha)}^2\sim\sigma^2\chi^2(n)\).
一般的,\(X_{(\alpha)}\sim N_p(\mu_\alpha,\Sigma),(\alpha=1,...,n)\)相互独立,记
则称\(W=X'X\)服从非中心参数为 \(\Delta=M'M=\sum\mu_{\alpha}\mu_{\alpha}'\)的非中心威沙特分布,记为\(W\sim W_p(n,\Sigma,\Delta)\)。
性质
- 设\(X_{(\alpha)}\sim N_p(0,\Sigma),(\alpha=1,...,n)\)相互独立,则样本离差阵\(A\)服从威沙特分布,即:
- 设 \(W_i\sim W_p(n_i,\Sigma),(i=1,...,k)\)相互独立,则
其中 \(n=n_1+\cdots+n_k\).
- 设\(p\)阶随机阵\(W\sim W_p(n,\Sigma)\).C是\(m\times p\)常数阵,则\(m\)阶随机阵\(CWC'\)也服从威沙特分布,即:\(CWC'\sim W_m(n,C\Sigma C')\).
- \(aW\sim W_p(n,a\Sigma),(a>0,为常数)\);
- 设 \(l'=(l_1,...,l_p)\),则\(l'Wl=\xi\sim W_1(n,l'\Sigma l)\),即:\(\xi\sim\sigma^2\chi^2(n)\),其中:\(\sigma^2=l'\Sigma l\).
- 分块威沙特矩阵:
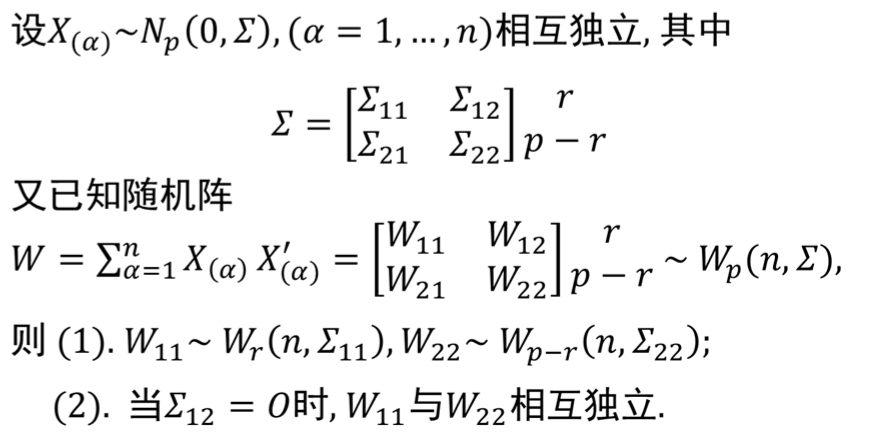

 从卡方分布扩展到了威沙特分布,三个重要统计量之首
从卡方分布扩展到了威沙特分布,三个重要统计量之首

 浙公网安备 33010602011771号
浙公网安备 33010602011771号