【施工中】一致收敛

一种更强的收敛

一致收敛性是一个在级数、积分运算中经常可以用到的性质，不过高数上并非重点，本文意在整理其定义，以及用通俗的语言描述常用的重要性质，最后一节给出一致收敛函数的判别法。

同时要注意区分数列收敛，函数列一致收敛及内闭一致收敛的区别，这些是初学者容易混淆的概念，应加以注意。

首先声明函数列及函数项级数的定义：

• 设\(f_1，f_2,\cdots,f_n,\cdots\)是一列定义在同一数据集\(E\)的函数，称为定义在\(E\)上的函数列\(\{f_n\}，（n=1,2,\dots）\),设\(x_0\in E\)，带入函数列可得到数列：

\[f_1(x_0),f_2(x_0),\cdots,f_n(x_0),\dots\tag{1} \]

• 对于上述函数列，称：

\[\sum_{n=1}^{\infty}f_n(x)=f_1(x)+f_2(x)+\cdots f_n(x)+\cdots，x\in E \]

为定义在\(E\)上的函数项级数，简记为\(\sum f_n(x)\)，称

\[S_n(x)=\sum_{k=1}^n f_k(x)，x\in E，n=1,2,\dots \]

为函数项级数的部分和函数列

若数列（1）收敛，则称函数列在\(x_0\)收敛，若函数列在数集\(D\sub E\)上每一个点都收敛，则称函数列在数集 D 上收敛。即对于\(\forall x\in D\)，存在数列\(\{f_n\}\)的极限值与之相对应，由此映射所对应的 D 上的函数，称为函数列的极限函数，记为：

\[\lim_{n\to\infty}f_n(x)=f(x)，x\in D\sub E \]

\[for\ x\in D,\forall\varepsilon>0,\exist N>0,s.t.n>N\ 时\\ |f_n(x)-f(x)|<\varepsilon \]

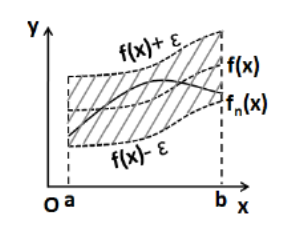
函数列的一致收敛性

设函数列\(\{f_n\}\)与函数\(f\)定义在同一数集\(D\)上，若对任给的正数\(\varepsilon\)，总存在某一正整数 N ，使得当\(n>N\)时，对一切\(x\in D\),都有：

\[|f_n(x)-f(x)|<\varepsilon \]

则称函数列\(\{f_n\}\)在 D 上一致收敛于\(f\)，记作：

\[f_n(x)\rightrightarrows f(x)\quad(n\to\infty)，x\in D \]

## approach to judge

函数列 一致收敛的柯西准则

函数列\(\{f_n\}\)在数集\(D\)上一致收敛 \(\Leftrightarrow\) 对\(\forall\varepsilon>0,\exist N>0\)使得当\(n,m>N\)时，对一切\(x\in D\)都有：

\[|f_n(x)-f_m(x)|<\varepsilon \]

[必要性]

设

\[f_n(x)\rightrightarrows f(x)\quad(n\to\infty)，x\in D \]

由定义，即对\(\forall\varepsilon>0,\exist N>0\)使得当\(n>N\)时，对一切\(x\in D\)都有：

\[|f_n(x)-f(x)|<\frac{\varepsilon}2 \]

于是当\(n,m>N\)时，由上式：

\[|f_n(x)-f_m(x)|\leq|f_n(x)-f(x)|+|f(x)-f_m(x)|<\frac{\varepsilon}2+\frac{\varepsilon}2=\varepsilon \]

[充分性]

若\(|f_n(x)-f_m(x)|<\varepsilon\)成立

函数列 一致收敛的充要条件

内闭一致收敛性

函数项级数的一致收敛性判别法

一致收敛的柯西准则

函数项 级数一致收敛的充要条件

Weierstraß 判别法

Abel 判别法

Dirichlet 判别法

一致收敛函数列的性质

• （极限顺序无关性）设函数列\(\{f_n\}\)在\((a,x_0)\bigcup(x_0,b)\)上一致收敛于\(f(x)\)，且对于每一个n，\(f_n(x)\to a_n\quad(x\to x_0)\)，则\(\{a_n\}(n\to\infty)\)和\(f(x)\ (x\to x_0)\)均存在且相等。

也就是说，在一致收敛的情况下，\(\{f_n(x)\}\)中的两个独立变量\(x、n\)再分别求极限时其求极限的顺序可以交换。

\[\lim_{x\to x_o}\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}\lim_{x\to x_o}f_n(x) \]

• （可积性）设函数列\(\{f_n\}\)在\([a,b]\)上一致收敛，且每一项都连续，则

\[\int_a^b\lim_{n\to\infty}f_n(x)dx=\lim_{n\to\infty}\int_a^bf_n(x)dx \]

在一致收敛的情况下，极限运算与积分运算的顺序可以交换。

• （可微性）设函数列\(\{f_n\}\)在\([a,b]\)上有定义，若\(x_0\in[a,b]\)为\(\{f_n\}\)的收敛点，\(\{f_n\}\)的每一项在\([a,b]\)上都有连续的导数，且\(\{f_n'\}\)在\([a,b]\)上一致收敛，则：

\[\frac{d}{dx}{(\lim_{n\to\infty}f_n(x))}=\lim_{n\to\infty}\frac{d}{dx}f_n(x)\\ f'(x)=\lim_{n\to\infty}f_n'(x) \]

• （连续性）若函数项级数\(\sum u_n(x)\)在区间\([a,b]\)上一致收敛，且每一项都连续，则其和函数在\([a,b]\)上也连续

\[\sum(\lim_{x\to x_0}u_n(x))=\lim_{x\to x_0}(\sum u_n(x)) \]

• （逐项求积）若函数项级数\(\sum u_n(x)\)在区间\([a,b]\)上一致收敛，且每一项都连续，则：

\[\sum\int_a^bu_n(x)dx=\int_a^b\sum u_n(x)dx \]

• （逐项求导）若函数项级数\(\sum u_n(x)\)在区间\([a,b]\)上每一项都有连续的导函数，\(x_0\in[a,b]\)为\(\sum u_n(x)\)的收敛点，且\(\sum u'_n(x)\)在\([a,b]\)上一致收敛，那么：

\[\sum (\frac{d}{dx}u_n(x))=\frac{d}{dx}(\sum u_n(x)) \]