科技活动心得

名字是抄那个本子上的，那个本子太小了就写这里。

2022-06-25

[JLOI2016]圆的异或并

发现只要考虑圆与圆的包含关系，设第 $i$ 个圆被 $b_i$ 个圆包含，然后可得：

$\displaystyle ans=\sum_{i=1}^{n} (-1)^{b_i} r_i^2$

考虑扫描线，我们将把圆拆成上圆弧和下圆弧，用扫描线去截圆弧上的点，这样就可以知道圆与圆的包含关系了。

具体做法是，我们将圆按 x 坐标排序，将圆分为前端和后端，前端插入，后端删除，每次插入点前，先找到上圆弧的前驱（即离上半圆最近的下面的半圆），如果这是下圆弧，则包含于前驱，否则和前驱并列，再插入圆弧。

用 set 维护交点。

注意，为了防止元素重复，在写比较函数时，上圆弧和下圆弧加一个 $eps$ 扰动一下。

bool operator <(const node &bb) const {
	long double di1,di2;
	if(opt==0) di1=1.000*sqrt((long double)r*r-(long double)(nx-x)*(nx-x)+eps)+1.000*y;
	else di1=y-1.000*sqrt((long double)r*r-(long double)(nx-x)*(nx-x)+eps);

	if(bb.opt==0) di2=1.000*sqrt((long double)bb.r*bb.r-(long double)(nx-bb.x)*(nx-bb.x)+eps)+1.000*bb.y;
	else di2=bb.y-1.000*sqrt((long double)bb.r*bb.r-(long double)(nx-bb.x)*(nx-bb.x)+eps);
	return di1-di2<-eps;
}

set操作待复习

2022-06-26

[NOI Online #2 提高组] 游戏

恰好有 $k$ 个非平局不好算，我们算至少有 $k$ 个非平局的。

考虑设 $dp_{i,k}$ 表示 $i$ 的子树内有 $k$ 个非平局的方案数，$col_{i,0/1}$ 表示 $i$ 的子树内 $0/1$ 两种点的个数。

先从子树合并，枚举子树 $v$，则有：

$\displaystyle dp_{i,k+l} \to \sum_{k=0}^{\min(col_{i,0},col_{i,1})} \sum_{l=0}^{\min(col_{v,0},col_{v,1})} dp_{i,k}\times dp_{v,l}$

这里要注意之前的值不要被覆盖。

最后考虑节点 $i$ 被选为非平局的方案：

$\displaystyle dp_{i,k} \to dp_{i,k}+dp_{i,k-1}\times (col_{i,\neg c_{i}}-k+1)$。

注意 $col_{i,0/1}$ 的值要随 $dp_{i,k}$ 的合并过程更新，而不是预处理，预处理之后可能会 T。

然后设 $g_{k}$ 表示至少有 $k$ 局非平局的方案数，$f_{k}$ 是恰好有 $k$ 个非平局的方案数。

那么 $\displaystyle g_{k} = dp_{1,k} \times (\frac{n}{2} - k)!$，$\displaystyle (\frac{n}{2} - k)!$ 就是从剩下的点中随便取得方案数（我们把 $A$ 的点固定，用 $B$ 的点去匹配每个 $A$ 的点，方案数就是 $\displaystyle (\frac{n}{2} - k)!$）。

容斥一下，就有：

$\displaystyle f_k=\sum_{i=k+1}^{m} (-1)^{i-k} \binom{i}{k} g_i$

广义容斥，背包带复习……

[HNOI2016]序列

一道莫队（有在线做法但我不会）

众所周知，我们只要考虑 $r+1$ 会对 $[l,r]$ 的答案产生怎样的贡献就行了。

不难发现 $r+1$ 对区间的贡献是一段一段的，我们可以一段一段的算。

我们先找到 $[l,r]$ 的最小值，假设它的位置为 $p$，那么以 $p$ 之前的位置为子串的最小值一定是 $a_p$，把这一段贡献一起加了。

对于 $[p+1,r+1]$ 这一段的贡献，我们也想到一段一段的算，因此我们处理出了一个数组 $pre_i$ 表示 $i$ 往前第一个比他小或等于他的数。

那么我们就跳 $pre_i$，然后每段贡献加起来。

这样理所当然的 T 了。

我们考虑用一个前缀的形式去算，设 $f_p$ 表示以 $p$ 为右端点，$[1,p-1]$ 为左端点的区间的最小值之和。

用上面的思路，可以得出 $f_p = f_{pre_p} + a_p\times (p-pre_p)$。

重点来了，因为 $p$ 是 $[l,r]$ 中最小的数，所以 $p$ 一定会出现在 $r$ 往前跳 $pre$ 的路径中，换句话说， $f_r$ 一定是间接从 $f_p$ 转移过来的，而 $f_r$ 却不一定是从 $f_{l-1}$ 转移过来的，因此 $f_r-f_p$ 就可以是 $r$ 对 $[p+1,r]$ 的贡献，而 $f_{r}-f_{l-1}$ 却不是 $r$ 对 $[l,r]$ 的贡献。

将 $pre_i$ 向 $i$ 连边，建成一棵树的话会好理解些。

其他情况同理。

莫队的核心在于分块和转移（~~不可以贺的地方~~）。

2022-06-27

[HEOI2016/TJOI2016]排序

我们将排好序的区间看成一个大块，用 set 维护这些块（这个类似 Chtholly Tree）。

对于每一个块，我们可以存下它是按从大到小还是从小到大排序，并用权值线段树维护区间内的元素。

假设我们要对一个新区间 $[l,r]$ 排序了，我们把 $l$ 从它原本所在的块中分离出来，这里要用到线段树分裂（类似于 fhq_Treap 的分裂），$r$ 同理。

然后，我们把 $[l,r]$ 之间的所有块合并起来，这里用线段树合并。

查询的时候我们只需把 $q$ 的线段树拆出来就行了。

注意，使用 set 时要注意迭代器是否失效（具体如将区间的权值线段树的根存在 $rt_l$ 里和分裂时先分裂 $r+1$，再分裂 $l$ ）。

[NOI2016] 区间

考虑先将每个区间都加进来，然后看看最大值是否大于 $m$，如果有，那肯定合法，否则不合法。

那么现在考虑，如何选择 $m$ 个区间？

有一种方式是选择尺取法，我们每次先向右选区间 $R$，选到最大值大于等于 $m$ 时就收手，然后删掉左边的区间，直到最大值小于 $m$，然后统计答案。

这样和双指针的复杂度一样都是 $O(n)$ 的。

为了方便计算题目中所说的权值，我们把区间按长度排序。

维护数轴，用线段树。标记永久化多爽，写啥离散化。

尺取法能解决的是一个有单调性的问题，即加到了一定阈值就会合法的问题。

[AGC039D] Incenters

先做几步转换。

首先，三角形的内心是将它三条角平分线与圆的另外三个交点所组成的三角形的垂心。

如图中的 $\triangle DEF$

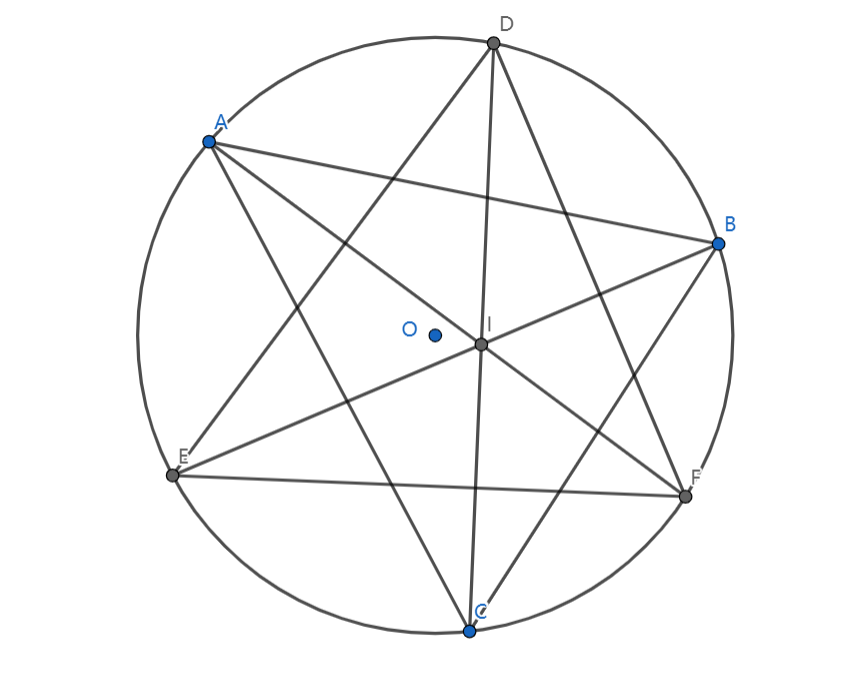
这极好证，随便导导角证垂直就证出来了。

然后，便是欧拉线，有 $OH=2OG$，如图：

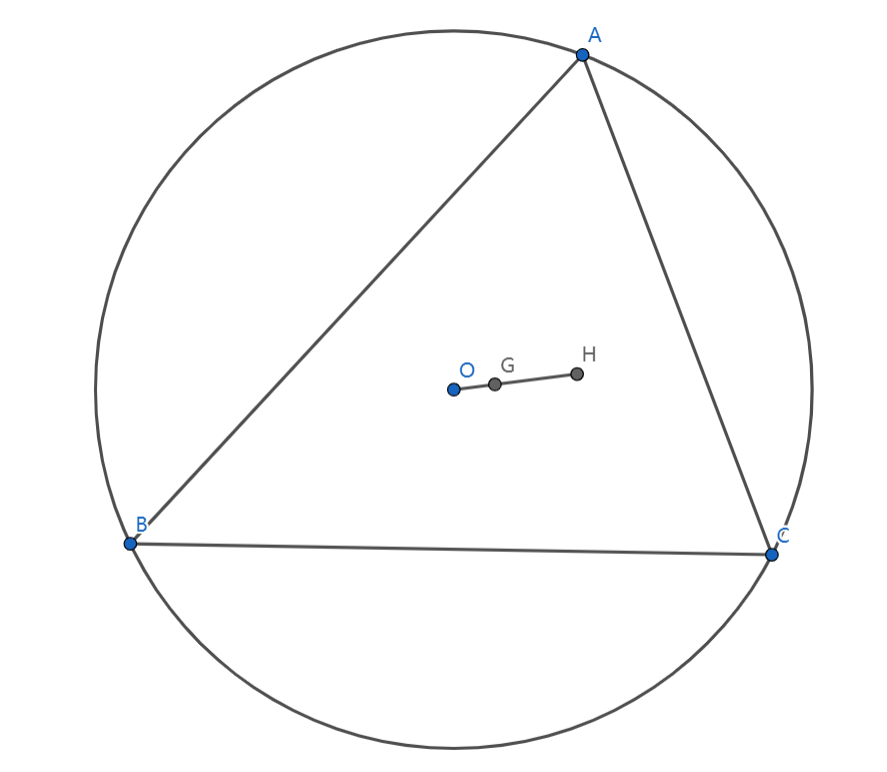
证明方法如下：

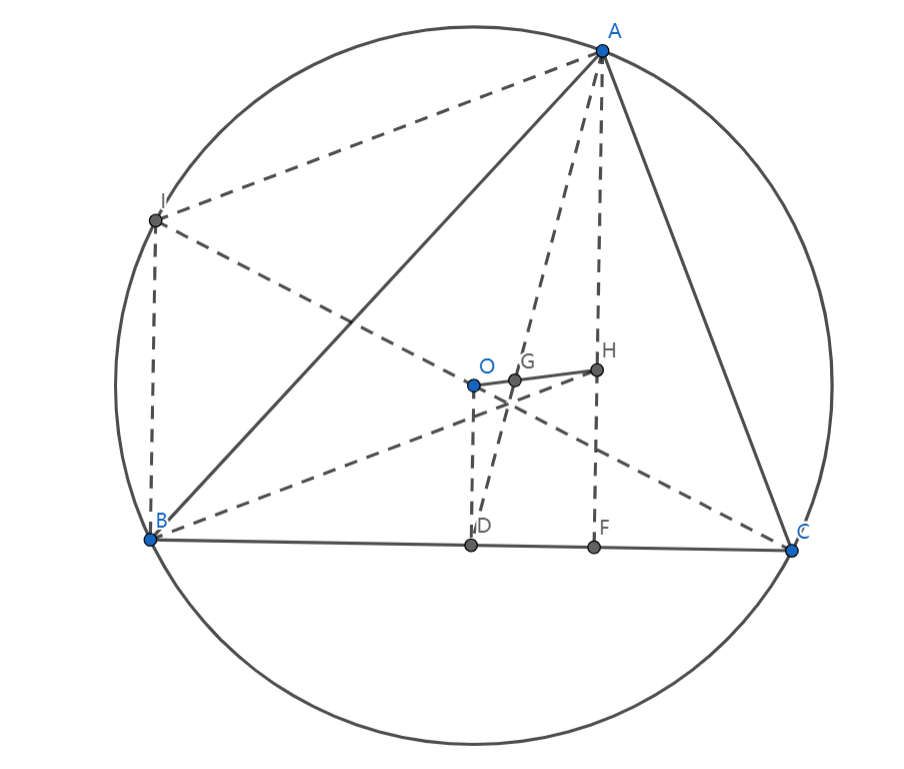
延长 $CO$ 交圆于点 $I$，连接 $IB,IA$，$D$ 是 $BC$ 中点，$F$ 是垂足，连 $AG,GD,OD,AH,HF,BH$。

考虑到 $CO$ 为直径，所以 $\angle IBC = 90^{\circ} ,\angle IAC= 90^{\circ}$，所以 $BI \parallel AH$，又因为 $\angle HBA= 90^{\circ} -\angle BAC,\angle IAB=90^{\circ} - \angle BAC$，所以 $\angle HBA=\angle IAB$，即 $BH\parallel AI$。

那么 $BI=AH$，因为 $OD$ 是中位线，所以我们有 $\displaystyle OD=\frac{1}{2}BI=\frac{1}{2}AH$，由重心性质可得 $AG=2GD$，通过相似我们可以得到 $O,G,H$ 三点共线且 $OG=2GH$。

所以 $\displaystyle \vec{OH}=3\vec{OG}$。

重心坐标公式是 $(\displaystyle \frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})$，因此 $H(x_1+x_2+x_3,y_1+y_2+y_3)$。

对于 $D,E,F$ 三点的坐标，我们可以结合鸡爪定理求出，即 $\displaystyle \bigg( cos\bigg(\frac{T_a+T_b}{2} \bigg),sin \bigg( \frac{T_a+T_b}{2} \bigg) \bigg)$（以 $D$ 为例，这里的 $T_a$ 指的是 $A$ 的极角）。

但是朴素做法是 $O(n^3)$ 的，所以我们考虑对于每两个点 $A,B$，算一遍他们对弦下方所有点的贡献和对弦上方所有点的贡献，这些可以直接加起来。

这样就变成了 $O(n^2)$，足已通过。

当然可以进一步优化，我们考虑对于横坐标的答案（令 $a_i = \frac{t_i\pi}{L}$）：

\[ans=\sum_{i=1}^{n} \sum_{j=i+1}^{n} \cos (a_i+a_j)(n-2i-2j) \\ =\sum_{i=1}^{n} \sum_{j=i+1}^{n} (\cos a_i \cos a_{j} - \sin a_i \sin a_j)(n-2i-2j) \\ =\sum_{i=1}^{n} \cos a_i \bigg( \bigg( (n-2i)\sum_{j=i+1}^{n} \cos a_j \bigg)-2\sum_{j=i+1}^{n} j\cos a_j \bigg) - \sin a_i \bigg( \bigg( (n-2i)\sum_{j=i+1}^{n} \sin a_j \bigg)-2\sum_{j=i+1}^{n} j\sin a_j \bigg) \]

纵坐标也按 $\sin(\alpha + \beta )$ 的公式拆开，结果和上面类似，这样我们只需统计 $\cos a_i,i\cos a_i,\sin a_i,i\sin a_i$ 的前缀和即可在 $O(n)$ 内求出答案。

基础思想：隔离魔鬼。

2022-06-28

[NOIP2021] 数列

这题状态明显难于转移。

考虑设 $f_{i,j,k,t}$ 表示已经考虑了 $S$ 的前 $i-1$ 位，已经填好了 $a$ 的前 $j$ 位，$S$ 在二进制下有 $k$ 个 $1$，且要向前进 $t$ 位的方案数。

前三维好想，第四位要注意到前面加上的数会对后面有影响。

考虑 $f_{i,j,k,t}$ 能转移给谁。

首先，后继状态的第一维一定是 $i+1$，相当于多考虑一位 $S$，然后考虑我们在 $i$ 这个位置上填 $l$ 个 $1$，那么在 $a$ 数组中就要填入 $l$ 个 $i$，所以转移的第二维就是 $j+l$。

考虑到每两个 $1$ 就会组成一个 $0$，因此转移后增加的 $1$ 的个数为 $(l+t)\bmod{2}$，向后进位的个数为 $\displaystyle \bigg\lfloor \frac{l+t}{2} \bigg\rfloor$。

因此 $\displaystyle f_{i,j,k,t} \to f_{i+1,j+l,(l+t)\bmod{2},\big\lfloor \frac{l+t}{2} \big\rfloor}$。

然后，考虑到乘积的相加可以拆开来成每一项然后加起来（乘法分配律）。

所以有：$\displaystyle f_{i+1,j+l,(l+t)\bmod{2},\big\lfloor \frac{l+t}{2} \big\rfloor} = v_i^l \binom{l}{n-j}f_{i,j,k,t}$。

转移即可，最后答案即 $\displaystyle\sum_{l=0}^{n}\sum_{t=0}^{\frac{n}{2}} [l+popcnt(t)\le k]f_{m+1,n,l,t}$（判断条件是因为要考虑向后进位）。

[ARC093C] Bichrome Spanning Tree

我们可以先建出最小生成树。

如果最小生成树的边权和 $val\le x$，我们肯定考虑用非最小生成树的边去凑出 $x$。

所以我们先将生成树上的边染成相同颜色。

但，我们只能强制选一条非最小生成树的边。这点很关键，我在这绕了好久，因为我们只需要两种颜色至少出现一次，那么假设树全被染成白色，我们将若干条非最小生成树的边染成黑色，那我们肯定会选择那条最小的黑色的边，剩下的按原来的最小生成树选，这样一定是最小生成树，其它的边就不够优而不会被选。

考虑每条非最小生成树的边替换掉最小生成树的边的增量。

很显然，对于一条非最小生成树的边 $(u,v,d)$，他的瓶颈（也就是在生成树上的路径 $(u,v)$ 中边权最大边）肯定是唯一能被它替换的边（这个思想可以参考次小生成树）。

设这个瓶颈的边权为 $lim$，那么这个增量就是 $d-lim$。

根据加粗字的结论，我们不能用多个边的增量凑出 $x$，我们只能选择一个增量使得 $d-lim+val=x$。

那么，为了防止这样的边被替换掉，我们要保证满足 $d-lim<x-val$ 的边都和生成树同一个颜色，$d-lim>x-val$ 的边随便染色。

设满足 $d-lim=x-val$ 的边有 $x_1$ 条，满足 $d-lim>x-val$ 的边有 $x_2$ 条。

那么方案数即 $2\times (2^{x_1}-1) \times 2^{x_2}$。

因为生成树和满足 $d-lim<x-val$ 的边的颜色有两种（黑和白），满足 $d-lim=x-val$ 的边的颜色不能全部与生成树和满足 $d-lim<x-val$ 的边颜色相同，因此 $-1$，剩下的边随便选。

当然，当 $val=x$ 时，我们就不一定要替换掉生成树上的边了（当然替换也是可以的），所以我们生成树上的边只要不是全部相同就行，然后非生成树的边还是随便染，方案数即 $(2^{n-1}-2)\times 2^{m-n+1}$。

对于 $val<x$，方案数只要算 $2\times (2^{x_1}-1) \times 2^{x_2}$，对于 $val=x$，我们要把上述两种情况加起来。

什么，你问 $val>x$？那不是 $0$ 吗？

这题可以用次小生成树那题的思想去思考，是为数不多我能独立想出大部分的 2500+。

~~但是倍增 LCA 竟然写挂了~~

倍增 LCA 在往上跳的时候，应该写 for(int i=19; i>=0; i--) 而不是 for(int i=19; i; i--)

2022-06-29

[AGC010F] Tree Game

我们发现根本没有思路，于是我们从只有两个点的情况入手。

假如先手选权值为 $a_1$，另外一个点权值为 $a_2$，那么显然只有 $a_1>a_2$ 的时候先手才会赢。

现在考虑一个菊花图的形式。

我们发现，假如叶子节点的权值有一个小于根节点的，那么先手一定会往那个节点上走，而后手无能为力，只能走回去，根据只有两个点的情况，此时先手必胜。

如果叶子节点的权值全部大于根节点，那么很显然的，无论先手往哪个节点走，先手的权值一定会被耗完（同两个点的结论）。

然后我们再来考虑更一般的情况。

对于叶子节点的父亲，我们显然可以把它当做菊花图的情况来处理。

而对于其他节点，我们假设已经求出了每个儿子的子树中是先手必胜还是后手必胜。

那么先手肯定不会往儿子节点中先手必胜的节点走，因为走了之后后手就可以把控全局。

因此先手会往儿子中后手必胜的节点走，但如果这个节点的权值小于先手选择的儿子节点的权值，后手一定会往回走，那么同只有两个节点的情况一样，先手会被耗死。

所以先手一定会往儿子中，有后手必胜的策略，且儿子节点权值小于父亲的走，这样后手就没有办法改变局面了。

于是我们可以 dfs 一下，枚举每一个点作为根，然后 dfs。对于每一个节点，找到儿子节点中具有后手必胜策略的权值最小的点，如果这个权值小于该节点的权值，则这个点的子树存在先手必胜策略，否则存在后手必胜策略。

然后换个根，维护一下最小值和次小值，就可以做到 $O(n)$。

此题的关键在于从特殊（简单）情况入手，化繁为简，再由特殊到一般，归纳得出做法。很多 AGC 都是这种思想。

[AGC010C] Cleaning

思考一下，我们发现对于每一个非叶子节点，能做的无非是这些：

内部消化一些石头，子树与子树之间相互匹配
将剩下的石头往父亲传，和父亲的其他儿子的子树解决。

因此我们考虑设一个状态 $f_{u}$，表示 $u$ 在子树内最大匹配之后，还需向父亲上传的石头。

我们发现，$u$ 的子树内能匹配多少，决定于 $u$ 的石头数量。

我们记 $sum_u$ 表示 $\displaystyle\sum_{v\in son_u} f_v$，即需要被解决的石头，我们发现，每消耗一个 $u$ 的石头，可以解决掉两个待匹配的石头，因此，我们有 $2a_{u}-sum_{u}=f_u$。

为什么不是 $sum_{u}-2a_u$ 呢？因为如果 $a_u$ 的石头个数都为 $0$ 了，那儿子节点的石头就上传不了了。所以，$f_u = 2a_{u}-sum_u \ge 0$，否则无解。

然后还有一个条件：$\displaystyle\max_{v\in son_u} f_v \le a_u$。为什么呢？仔细想想就会发现，每消耗一个 $u$ 的石头，儿子节点的需求就会减少 $2$，而对于选中的两个儿子节点，它们的 $f$ 只会分别减少 $1$，那么如果 $\displaystyle\max_{v\in son_u} f_v > a_u$ 的话，则会出现 $a_u = 0$ 从而使儿子节点上传不了的情况。

那为什么 $2a_{u}-sum_u \ge 0$ 没有把这种情况判掉呢？很显然，每个 $f_v$ 又不一样，比如 $f_v$ 分别为 ${5,2,1}$，$a_u=4$，那么 $2a_{u}-sum_u = 0$ 而 $\displaystyle\max_{v\in son_u} f_v > a_u$。

然后根节点的 $f$ 一定是 $0$，因为根节点已经无法上传了，否则无解。

注意到：

选择度数大于一的点为根。
叶子节点的 $f_u$ 赋成 $a_u$。
$n=2$ 的情况需特判。

思想仍是考虑每个节点然后递归解决。

[AGC010B] Boxes

通过约束建立方程思想，在 AT/CF Div2 的前几题比较常见。

我们考虑每次操作会把环的总权值减去 $\displaystyle\frac{n(n+1)}{2}$，所以我们判断环上所有点的权值和 $s$，如果 $\frac{n(n+1)}{2} \nmid s$ 就不合法。

设 $m=\displaystyle\frac{s}{\frac{n(n+1)}{2}}$

然后考虑我们处理出 $d_i=a_i-a_{i-1} (a_0 = a_n)$，不难发现如果我们对 $i$ 执行一次操作，那么 $d_i$ 就会加上 $n-1$，然而对于在其他点进行操作，$d_i$ 会减去 $1$，而我们最终要让 $d_i=0$。

我们设 $x_i$ 表示我们在节点 $i$ 进行了多少次操作，那我们不难发现一个方程：

\[\forall i \in [1,n],(m-x_i)-x_i(n-1)=d_i \]

则有：

\[\forall i \in [1,n],x_i=\frac{m-d_i}{n} \]

那我们只需每个判断 $x_i$ 是否是正整数，如果有一个不是就肯定不合法。

最后把所有 $x_i$ 加起来，如果不等于 $m$ 的话就不行，如果等于就一定构造的出方案。

2022-06-30

[AGC010D] Decrementing

从 $\gcd$ 下手十分困难，所以我们考虑序列中有 $1$ 的情况，这样问题就简单些了。

考虑对于如下情况：

$1,1,1,\cdots ,1,2,1,\cdots$

此时，先手（当前的）只需要把 $1$ 减掉，就赢了。

然后，我们考虑 $\cdots , 1 ,\cdots$ 的情况。

此时不论双方如何操作，最后这个序列的 $gcd$ 永远是 $1$，所以只需要考虑奇偶性。我们发现，如果 $2\nmid\displaystyle\sum_{i=1}^{n}(a_i-1)$ 则先手必胜，否则后手必胜，这个条件等价于有奇数个偶数。

那么考虑没有 $1$ 的情况。

如果此时数列中存在奇数个偶数，那么后手如果破坏一个偶数，先手就可以把它改回来，或者先手也破坏一个偶数或奇数；如果后手想要通过破坏奇数使得序列 $/ \gcd$，那先手可以在这之前把局面破坏掉，并在后面维护奇数个偶数。总之，偶数的奇偶性不会变，先手总能维持奇数个偶数。
如果此时数列中不存在奇数个偶数，但是，奇数只有一个（当然不是 $1$），那么先手就把这个奇数破坏掉，使得整体 $/ \gcd (2\mid\gcd)$，从而使整个局面发生很大的变化。这个时候，我们只需判断一下，然后模拟一下先手的操作，最后重新判断新的局面，每次至少除以 $2$，总次数不会超过 $\log$，注意此时后手反客为主了。
否则，后手就可以像先手那样操纵局面，从而使得后手必胜。

仍是从特殊出发，但重点是想到考虑偶元素数量的奇偶性，将原本难以下手的除以gcd变成了只要考虑奇偶性的简单问题。

[AGC010E] Rearranging

zy 布置给小六的题不会了~~话说现在小六都爆切 AT 银版题吗？~~

很神奇，我至今不知道正解怎么想到的。

考虑到先手能做的事情太多，我们从后手的操作入手。

可以发现，对于不互质的数，它们的相对关系已经被先手内定了，后手怎么做都是徒劳无功。

而且，不互质具有传递性和对称性，于是将不互质的数互相连边，然后~~我也不知道为什么~~想到先手的操作即是给这些边定向，把连通块变为 $DAG$，且使得对于每个连通块内的 $bfs$ 序的字典序最小（即是：总是从小数走到大数）。

然而根据后手的选法。对于不同连通块，甚至是统一连通块内互质的数（它们一定不会有边相连，且它们被遍历的顺序不会互相影响，我们可以理解为它们的拓扑序是一样的），后手都能够随意交换位置，那么我们可以想出一种后手的贪心策略：即每次选择值最大的入度为 $0$ 的点，然后模拟 topsort 的过程，即将 topsort 的队列改为大根堆。

这题的关键在于想到向连边后定向（或者说求字典序最小的 $bfs$ 序？），然后问题就很好解决了。

[AGC017D] Game on Tree

首先一看题，没有思路，发现第一个样例根只有一个儿子，那我们把它切掉不就好了？

然后对于两个儿子，我们考虑先手可以留着点东西切，然而后手也不敢贸然行动，那么就考虑当谁不得不把其中一条边断掉就输，这样可以把两个子树看做是子问题，递归处理。

然后想不到其他的了。

我们会发现，对于一个菊花图而言，它如果有奇数个儿子就先手必胜，偶数的话就后手必胜。

然后就联想到了，异或和？

然后有回到根只有一个或两个儿子的情况，如果有多颗这样的树，是不是有点像 Nim 游戏？

于是我想到了用 $sg$ 值来处理。

通过菊花图的情况，我猜测儿子的 $sg$ 值是不是要 $+1$ 才能参与异或，仔细一想发现是的。

我们把根的儿子取出来，再在每一个上面加上一个根节点，我们发现这就是多个独立游戏，那么总的 $sg$ 值就是这些 $sg$ 值得异或和。

对于每一个独立的游戏，我们考虑它一定有一个状态是必败状态，那便是切除根和惟一的儿子节点。

然而对于其他状态，我们可以试试数学归纳法。

我们发现，每切掉一条边，问题都会少一个规模，并且我们知道当我们划掉一个叶子节点时，就等价了在儿子的子树内玩游戏，那么我们可以考虑这个对博弈图分层，我们考虑当层数等于 $1$ 的情况（即必败状态的前一层），那么这个状态的 $sg$ 显然等于 $1$。

再对于第 $k$ 层，我们假设前 $k$ 层满足这个结论，那 $\displaystyle sg_{k+1}= \operatorname{mex}_{i=1}^{k} (sg_{i})$，我们会发现 $sg_{i}=sg_{i-1}+1,sg_{0}=0$，所以 $sg_{k}$ 及之前的数都有过了，那么$sg_{k+1}=sg_k +1$。

归纳得出只有一个根节点的游戏，它的 $sg$ 等于它的儿子的 $sg$ 值 $+1$。

听说这个很经典，可能当时学博弈论时题做少了。

[AGC023F] 01 on Tree

题目要求现删父亲，再删儿子，那么我们发现，只要父亲再前，儿子就可以随便排。

那我们把每棵子树看做一个子问题，对于一个节点的两个子节点 $s_1$ 和 $s_2$，如果把 $s_1$ 放前面，对答案的贡献就是 $cnt_{s_1,1}\times cnt_{s_2,0}$，反之则是 $cnt_{s_1,0}\times cnt_{s_2,1}$。

于是我们可以贪心的选，先选 $\frac{cnt_{u,1}}{cnt_{u,0}}$ 最小的 $u$。

于是我按这个写了，写着写着突然想：对于不同子树的不同节点，它们也是可以调换顺序的，比如再根的两颗子树 $T_i,T_j$ 中，有两个节点 $s_{i},s_j$，权值分别为 $0,1$，假设原先的顺序是把 $T_j$ 放到 $T_i$ 的前面，那我们将 $s_i$ 以及它的祖先们（假设祖先都是 $0$）调到 $s_j$ 的前面，显然就减少了答案。

然而贪心是没错的，只是需要考虑全局。

那我们不妨想出一个这样的算法：

先将每个点看做是独立的。

我们把所有点都扔到小根堆里，每次选出堆顶，然后并到它的父亲上所在的连通块上，计算贡献。显然，这个时候保证了父亲再它的前面，并且根据刚才的贪心，父亲连通块内的数列必然是最优的。

连通块可以用并查集维护。

但我们要考虑到一件事，如果我们把父亲所在连通块的 $cnt$ 改变了，那我们先得把堆中的父亲节点的祖先删掉，然后再更改它的权值，再插入，不然就保证不了堆的单调性。所以我们要写个可删堆。

当然这个我是不会写的，于是我~~看了一眼题解~~将取出的堆顶的 $cnt$ （这里是结构体中自带用来排序的）与他真实的 $cnt$ 数组（合并时改的是这个）比较，不合法就 continue。

PS：我当时把小根堆写成大根堆调了挺久。。。

2022-07-01

[AGC028C] Min Cost Cycle

乍一看好像挺神奇，我们肯定不能求直接求这个边权和最小的哈密顿回路的边权和，考虑将问题转换。

我们这样把题目改写一下：考虑确定一种点的顺序，使得 $\displaystyle\sum_{i=1}^{n}\min(a_i,b_{i+1}) \ (b_{n+1}=b_1)$ 最小。

进一步的，我们考虑将 $\min$ 变成起点 $i$ 和终点 $i+1$ 中任选一个（只要不是同时被选），这样可以使问题简单些。为什么可以呢？

考虑到如果 $a_i < b_{i+1}$ 而我们把 $b_{i+1}$ 选了的话，那么选 $a_i$ 的答案显然更优，所以选 $b_{i+1}$ 的情况就被舍去了。

我们先考虑一个方案是否合法。

我们不难发现，对于一个点 $u$，它对答案的贡献只有 $4$ 种：

$a_u$ 被选而 $b_u$ 不被选，我们记为 10
$a_u$ 不被选而 $b_u$ 被选，我们记为 01
$a_u,b_u$ 都被选，我们记为 11
$a_u,b_u$ 都不被选，我们记为 00

我们发现，一条边 $u \to v$，$a_u,b_v$ 是不可能同时被选的，既不可能出现 $1,0\to 0,1$ 或 $1,0 \to 1,1$ 或 $1,1 \to 0,1$，但有可能出现 $0,1\to 1,1$。

对于所有相连的 10 我们可以把它并成一个点，01 同理。

假设序列中只出现了 10 或 01，那肯定合法。但如果 10 和 01 同时出现却没有其它的，那一定不合法。

如果出现了 11，那么我们不难发现 00 的个数会和 11 相等。

于是我们可以考虑这样构造：01 11 10 00，然后 00 接 01。

我们发现，把所有 $a_i,b_i$ 排个序，选前 $n$ 个，如果合法，那么这样肯定是最优的。

如果不合法，为了最优，我们会考虑把第 $n$ 个换成第 $n+1$ 个。

如果还不合法，那我们有两种换发：

第 $n+1$ 换成第 $n+2$ 个。
第 $n-1$ 换成 $n$ 个。

这时一定合法，只需取 $\min$。

为什么？

首先不合法的情况肯定是只有 10 和 01，考虑换了一次还是不合法那必然是把 01 换成了 10 或反之。

那么我们便可以得出第 $n$ 个和第 $n+1$ 个是属于同一个点的权值。

那我们做第二次修改，便会制造出一个 11 或 00。

那就一定合法了。

关键是通过贪心保证合法，进而使得问题简化。

[AGC028B] Removing Blocks

自己写出来的，很开心。

考虑计算每一个区间 $[l,r]$ 的贡献（计算加上的值恰好是这个区间，可以证明这样不会重复也不会遗漏）：

对于 $l-1,r+1$，它们要在区间内的点被选之前选，然后 $[1,l-1),(r+1,n]$ 中的点随便放，那我们便会有一个计算方案数的式子：

\[T=2(r-l+1)!\times A(n,r-l+3) \]

然后再乘上区间和。

当区间为端点为 $1$ 或者是 $n$ 时要单独算。

考虑优化。

我们先把区间为端点为 $1$ 或者是 $n$ 时单独算了。

然后考虑先枚举长度：

\[\sum_{len=1}^{n} \sum_{i=2}^{n-len} (sum_{i+len-1}-sum_{i-1})\times 2len!\times A(n,len+2) \]

把 $T$ 提出来：

\[\sum_{len=1}^{n} T\sum_{i=2}^{n-len} (sum_{i+len-1}-sum_{i-1}) \]

我们不难发现 $\displaystyle\sum_{i=2}^{n-len} (sum_{i+len-1}-sum_{i-1})$ 展开来就是 $sum_{len+1}-sum_1+sum_{len+2}-sum_2+\cdots +sum_{n-1}-sum_{n-len-1}$。

那我们做一做加法交换律，就得到：

\[\sum_{i=2}^{n-len} (sum_{i+len-1}-sum_{i-1}) = \bigg( \sum_{i=len+1}^{n-1} sum_i\bigg) - \bigg( \sum_{i=1}^{n-len-1} sum_i \bigg) \]

维护 $sum_i$ 的前缀和和后缀和，就可以很快计算。

又是隔离魔鬼。

不过题解为什么都是神仙期望做法？

[AGC028D] Chords

考虑把这个环上的问题转到序列上，对于两条边 $(u_1,v_1)$ 和 $(u_2,v_2)$，把它们看做区间，如果它们相交但不包含，则它们在圆上也相邻。

我们可以考虑到找到一个连通块的标号最小点 $i$，和标号最大点 $j$，设一个状态 $f_{i,j}$ 表示 $[i,j]$ 这个连通块被算了多少次，显然有：

\[f_{i,j} = g(c_{i,j})*g(2n-j+i-1-2k+c_{i,j}) \]

$g(n)$ 表示 $n$ 个点随便连边的方案数，可以发现 $2\nmid n$ 时 $g(n)=0$，否则 $g(n)=(n-1)g(n-2),g(0)=1$，于是我们可以预处理 $g$。$c_{i,j}$ 表示 $[i,j]$ 内未被确定的点的个数。

当然不止上述这些，还有其他情况：

当 $[i,j]$ 内存在一个点连到了 $[i,j]$ 外（是题目中钦定的连边），那 $[i,j]$ 这个连通块就不复存在了，方案数为 $0$。
可能 $[i,j]$ 内是由小连通块组成的，我们可以考虑容斥：$\displaystyle f_{i,j}=g(2n-j+i-1-2k+c_{i,j})(g(c_{i,j})-\sum_{k=i}^{j} f_{i,k}*g(c_{k+1,j}))$。

最后把所有 $f_{i,j}$ 加起来就是答案。

这题挺妙的，把相交问题转化为区间问题，然后用类区间 Dp 的思想求答案。

2022-07-04

笔记前五题。

2022-07-05

笔记后两题。

2022-07-06

Count on a tree

主席树板子。

注意要减去 siz[lca]+siz[fa[lca]]，而不是只减 siz[lca]。

帕秋莉的魔导书

求期望可以转成求前缀和的区间和，那维护前缀和数组不就好了？

每次加入一个数，就相当于一个区间加。

[PKUWC2018]Minimax

大佬们都是先做这再在考场上秒掉 NOI2020 D2T1，而我先做了命运再做这个的。

先考虑一个 $O(nw)$ 的 DP。题目中要我们求的那玩意肯定不好维护，我们还是维护每个数的出现概率。

设 $f_{i,j}$ 表示 $i$ 的权值为 $j$ 的概率。

假设 $j$ 是左儿子的权值，那概率先得是 $f_{ls,j}$，然后还得保证它一定会被选，考虑 $i$ 是选最大值还是最小值。

因为左子树已经被确定了，所以我们考虑右子树的被选择情况

$j$ 是最大值的概率显然是 $\displaystyle\sum_{k=1}^{j-1} f_{rs,k}$，当然还得 $i$ 选最大值，所以乘上一个概率 $p_i$，$j$ 是最小值的话同理，即 $\displaystyle\sum_{k=j+1}^{w} f_{rs,k}$，再乘上 $1-p_i$。

右子树一样的考虑。所以我们就有了转移：

\[f_{i,j} = f_{ls,j}\left( p_i\sum_{k=1}^{j-1} f_{rs,k} + (1-p_i)\sum_{k=j+1}^{w} f_{rs,k}\right) + f_{rs,j}\left( p_i\sum_{k=1}^{j-1} f_{ls,k} + (1-p_i)\sum_{k=j+1}^{w} f_{ls,k}\right) \]

我们发现几个 $\sum$ 都是前缀和或后缀和的形式，并且状态出现了两维，因此我们考虑用一种结构动态维护前缀和和后缀和，同时维护整个数列，这里我们使用线段树。

考虑线段树合并。

因为题目中说权值不会重，所以我们在做线段树合并的过程中，不是左儿子的线段树在这个节点上为 $0$，就是右儿子为 $0$。

以左儿子为 $0$ 为例，所以此时 $\displaystyle f_{i,j}=f_{rs,j}\left( p_i\sum_{k=1}^{j-1} f_{ls,k} + (1-p_i)\sum_{k=j+1}^{w} f_{ls,k}\right)$，对于括号内的值是可以通过维护前缀和和后缀和求出来的，所以直接更新即可。不过注意此时这个节点可能是一个区间，所以我们直接打上乘法标记。

那前缀和和后缀和怎么维护呢？

有一种方法是，将前缀和和后缀和写入函数的参数中，递归左儿子（这里是线段树上的节点，前面是原树上的节点）时，将该节点后缀和加上右儿子的权值和然后递归；递归右儿子同理。

2022-07-07

[SDOI2011] 消耗战

虚树板子。

考虑 DP，设 $dp_{i}$ 表示 $i$ 与子树内的的点切开的最小代价。

不难得出：

\[dp_{u} = \begin{cases}dp_{u}+w_{u,v}&v \ \operatorname{is} \ \operatorname{keynode} \\dp_{u}+\min \{dp_v,w_{u,v}\}&\operatorname{otherwise}\end{cases} \]

然后发现每次对关键点建虚树即可。

虚树的边权为原来树上两点间的最小边权。

[NOI2014] 起床困难综合症

简单贪心。

这种关于位运算的一般按位考虑。

考虑用两个数，一种存下二进制下全 $0$ 通过门之后的值（记为 $a_0$），一种存下二进制下全 $1$ 通过门之后的值（记为 $a_1$）。

然后考虑求答案，为了使答案更大，我们从高位到低位枚举。

如果 $a_0$ 这一位为 $1$，那说明答案这一位肯定能为 $1$。

如果 $a_1$ 这一位为 $1$，那我们能加就加，这样一定是最大的。

关于位运算的一般按位考虑。

[Ynoi2017] 由乃的 OJ

绿题上树。

肯定考虑沿用上道题的贪心，这时你会发现合并不好做，并且可能是 $O(nk\log^2 n)$ 的东西，复杂度很悬。

我们先考虑合并，也就是维护线段树的问题。

我们考虑对每个区间，维护四个值：$l_0,l_1,r_0,r_1$，定义同上题 $a_0,a_1$ 类似，只不过 $l_0,l_1$ 是从区间左边开始走，$r_0,r_1$ 是从区间右边开始走。

为什么呢？

因为你在查询树上路径的时候，$x \to lca$ 是 $dfn$ 倒序的，而 $lca\to y$ 是 $dfn$ 正序的。

然后考虑合并。

我们发现（这里是考虑某一位）：

$ls[l_0]=1,rs[l_1]=1\Rightarrow p[l_0]=1$
$ls[l_0]=0,rs[l_0]=1\Rightarrow p[l_0]=1$
$ls[l_1]=0,rs[l_0]=1\Rightarrow p[l_1]=1$
$ls[l_1]=1,rs[l_1]=1\Rightarrow p[l_1]=1$

$r$ 同理。

于是我们可以得到这样的合并方法：

node operator +(const node &bb) const {
	node res;
	res.l0=(l0&bb.l1)|((~l0)&bb.l0);
	res.l1=(l1&bb.l1)|((~l1)&bb.l0);
	res.r0=(bb.r0&r1)|(r0&(~bb.r0));
	res.r1=(bb.r1&r1)|(r0&(~bb.r1));
	return res;
}

维护了这玩意之后，我们显然可以把贪心放到最后，最后就变成了 $O(n\log{n}+q(\log^2{n}+k))$。

调试心得：

我把树链剖分跳 top 写成了这玩意：

while(fx!=fy) {
	if(dep[fx]>dep[fy]) {
		ans1[++cnt1]=wgj.query(1,n,1,dfn[fx],dfn[u]);
		u=top[fx];
		fx=top[u];
		}
	else {
		ans2[++cnt2]=wgj.query(1,n,1,dfn[fy],dfn[v]);
		v=top[fy];
		fy=top[v];
	}
}

注意位运算时要写 `1ull`。

正确：

if((vv.l0>>i)&1ull) ans=(ans+(1ull<<i));
else if(((vv.l1>>i)&1ull)&&z>=(vi+(1ull<<i))) ans=(ans+(1ull<<i)),vi=vi+(1ull<<i);

错误：

if((vv.l0>>i)&1) ans=(ans+(1<<i));
else if(((vv.l1>>i)&1)&&z>=(vi+(1<<i))) ans=(ans+(1<<i)),vi=vi+(1<<i);

注意 ull 不能减出负数！！！

P5174 圆点

考虑枚举 $\frac{1}{4}$ 圆然后再乘 $4$。

先枚举横（纵也可以）坐标，可以用勾股定理求出这一行（列）的整点个数：$\lfloor\sqrt{r-i^2}\rfloor$。

然后考虑算贡献：

\[ans=\sum_{i=1}^{\sqrt{r}} \sum_{j=1}^{\lfloor\sqrt{r-i^2}\rfloor} i^2+j^2 \\ =\sum_{i=1}^{\sqrt{r}} \lfloor\sqrt{r-i^2}\rfloor i^2 + \sum_{j=1}^{\lfloor\sqrt{r-i^2}\rfloor} i^2+j^2 \\ =\sum_{i=1}^{\sqrt{r}} \lfloor\sqrt{r-i^2}\rfloor i^2 + \frac{\lfloor\sqrt{r-i^2}\rfloor (\lfloor\sqrt{r-i^2}\rfloor +1)(2\lfloor\sqrt{r-i^2}\rfloor +1)}{6} \]

2022-07-08

[POI2011]ROT-Tree Rotations

考虑到对于每一个节点，合并两棵子树的答案时，每棵子树内的权值顺序不会影响这个节点增加的答案。

于是我们可以想到线段树合并。

然后这题做完了。

这种 ex 的读入使得我需要边读入边计算答案。

[THUWC2017]在美妙的数学王国中畅游

如果不给泰勒展开公式，我不一定会往把函数用多项式表示的方面去想。

不过这里给了，那它就是 nt 缝合题了。

考虑到肯定要用 LCT 之类的数据结构维护。

那么，快速的将路径上的信息合并，或者快速求出经过路径后的函数值，是最为严重的问题。

因为，我们很难把一个包含 $\operatorname{Exp},\sin ,ax+b$ 的函数合并起来处理，也没有办法快速求值。

~~那么我们只能贺题解了~~

当然我们不是法国人，我们把题目往下翻翻，发现出题人给了你这个：

【小R 教你学数学】

若函数 $f(x)$ 的 $n$ 阶导数在 $[a,b]$ 区间内连续，则对 $f(x)$ 在 $x_0 \ (x_0\in[a,b])$ 处使用 $n$ 次拉格朗日中值定理可以得到带拉格朗日余项的泰勒展开式

\[f(x)=\sum_{k=0}^{n-1}\frac{f^{(k)}(x_0)(x-x_0)^k}{k!}+\frac{f^{(n)}(\xi)(x-x_0)^n}{n!},x\in[a,b] \]

其中，当 $x>x_0$ 时，$\xi\in[x_0,x]$。当 $x<x_0$ 时，$\xi\in[x,x_0]$。

$f^{(n)}$ 表示函数 $f$ 的 $n$ 阶导数。

想想，泰勒展开是不是将函数用多项式表示的一种手段，那么我们可以对 $\operatorname{Exp},\sin$ 这两个函数进行泰勒展开。

我们都知道：$(e^x)^{\prime}=e^x,\sin{x}^{\prime}=\cos{x},\cos{x}^{\prime}=-\sin{x}$。

于是我们让 $x_0=0$，这样就有：

\[\operatorname{e}^{ax+b} = \sum_{i=0}^{\infty} \frac{(ax+b)^i}{i!} \\ \sin (ax+b) = \sum_{i=0}^{\infty} \frac{(-1)^{2i+1}(ax+b)^{2i+1}}{(2i+1)!} \]

我们考虑到 OI 只要求我们算近似值，所以我们取这个多项式的前几项就可以了，我取的是 $15$。

然后只需将多项式的系数加起来，求值即可。

再套个 LCT 板子。

2022-07-10

Meeting

考虑求出以 $1$ 为起点的最短路和以 $n$ 为起点的最短路，然后枚举每一个点算答案。

不过这个连边最坏情况是 $O(n^2)$ 的，所以我们考虑优化建图。

使用一个虚点连每一个块，就结束了。

挺 nt 一题，因为 PE 调了很久（说句闲话，上次遇到 PE 还是在初一，而现在我高一了）。

[POI2015] PUS

考虑对每个位置的大小约束关系连边，然后 topsort 检验。

检验数的大小关系是否矛盾，即判环。
检验是否能满足原本规定的值，这个可以用 DP 做，设 $f_{i}$ 表示 $i$ 的最小权值，初始时有值就赋值为那个值，没有就没有。然后在 topsort 的过程中由相连的节点转移过来，即 $f_{v}=max(f_{v},f_{u}+1)$。
检验是否超出值域范围，也是上面 DP。

然后套个线段树优化建图即可（也要一个区间一个区间的连）。

Counting Stars

三元环记数。

考虑如果一条边被 $k$ 个三元环包含，就会产生 $\binom{k}{2}$ 的贡献。

于是我们统计每一条边被算了几次即可。

我们可以将三元环的边拆成三类分别处理。

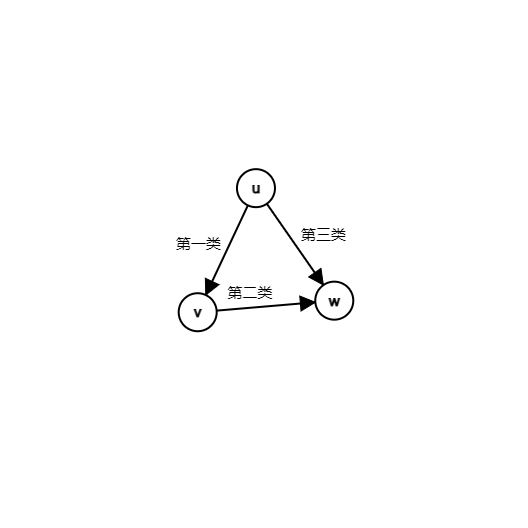
第二类先统计，先枚举与 $u$ 相连的 $v$，再枚举与 $v$ 相邻的 $w$，然后顺便统计三元环个数。
第一类，考虑我们每枚举一个 $v$ 时，能算出包含 $u,v$ 的所有三元环，然后加到 $(u,v)$ 的贡献中就是了。
第三类，我们在枚举 $w$ 时对每个 $w$ 打上一次标记，最后统计所有与 $u$ 相连的点的标记。

[SDOI2009] Elaxia的路线

我们先做两遍最短路，于是我们有了两张最短路构成的 DAG。

考虑到重合的路径一定会是连续的，所以我们可以在 topsort 时 DP 处理。

然后我们考虑到重合路径有两种情况：

两者同向。
两者异向。

于是我们在开头处理出四个点的最短路，再根据上面两种情况连有向边，最后跑 topsort 统计链的长度。

还是有一定思维含量的吧。

2022-07-11

太摸了今天，只写了一道题（糊倒是糊了三道）

CF985G Team Players

显然建反图边数是 $O(n^2)$ 的，不能使用这种方法。

考虑容斥。

它是要恰好没有边相连，我们仍然可以求钦定 $n$ 条边相连的 $g(n)$，然后 $ans=g(0)-g(1)+g(2)-g(3)$。

$g(0)$ 是钦定 $0$ 条边相连，我们可以先求 $i\times A$ 的前缀和 $sumA_{i}$，再求 $i\times B+sumA_{i}$ 的前缀和 $sumB_{i}$，再求 $i\times C+sumB_{i}$ 的前缀和。
对于 $g(1)$，我们可以枚举每条边 $(u,v)$，然后讨论 $[1,u),(u,v),(v,n]$ 算贡献。
对于 $g(2)$，我们可以枚举每个点 $u$，然后将 $u$ 的边排序后，用类似 $g(1)$ 的方式分类讨论，注意到每条边都被算了两次，贡献也就被算了两次，所以要除以二。时间复杂度：$\displaystyle\sum_{i=1}^{n} deg_i\log{deg_i} = O(m\log{m})$。
对于 $g(3)$，我们直接枚举三元环然后统计答案。

PS:早上算 $g(2)$ 时建有向图调了一早上，下午枚举三元环时三个点的排序写错调了一下午。。。

对这一天的反思： 留给我的时间不多了，还是要抓紧，不能总是在犹豫哪题代码好写，也不能在工作时间摸鱼。

2022-07-12

[POI2013]CEN-Price List

我们先考虑答案来源。

有可能，答案是原图上的最短路（即全是 $a$），也有可能，我们将两个 $a$ 替换成一个 $b$，不过最后可能余下 $a$。

当然还有一种可能，我们多走了几个 $b$，从而绕过了余下的 $a$。

对于前两种，bfs 即可。

对于后一种，我们考虑枚举 $u$ 的相邻节点 $v$ 的相邻节点 $w$，用 $u$ 的值去更新 $w$。

但这样是 $O(m^2)$ 的，考虑优化。

考虑 $u\to v$ 和 $v\to w$，当我们用 $u$ 更新 $w$ 之后，对于其它点 $s \to v$，再枚举 $v \to w$ 就是没有必要的，于是我们可以把这条边删了。

不过在枚举 $v$ 的相邻节点的相邻节点时，这条边还是有用的，所以我们存两幅图，第一幅用于第一次遍历，第二幅用于第二次遍历。

这样每个三元环只会被枚举一次，套用三元环计数的结论可以得到复杂度是 $O(m\sqrt{m})$ 的。

PS：关键是想到三元环计数的优化策略。

[POI2013]MOR-Tales of seafaring

思路同 CSP-J 2019 T4。

考虑要是 $d$ 能被凑出来，那么 $2k+d$ 也能被凑出来。

于是求出长度为奇的和长度为偶的最短路，然后判断询问路径长度的奇偶性，看路径长度是否大于对应奇偶性下的最短路。

求奇偶最短路的一种方法是拆点后 bfs。

考虑到空间不够，开 short 压。

还有一种情况需要考虑：当询问的 $s,t$ 相同，且 $s$ 是孤点时，即是 $d$ 为偶数不能构造方案，要特判。

其它情况均不需特判

PS：对于 $s=t$ 的情况瞎判导致我调了好久。

[AHOI2014/JSOI2014]骑士游戏

我觉得挺好一思维题。

考虑 DP。

设 $dp_{i}$ 表示 $i$ 被完全打败的价值，那么有 $\displaystyle dp_{i}=\min \{ k_{i},s_{i}+\sum_{v\in R_i} dp_{v_i}\}$。

但直接转移有后效性，我们考虑怎么消除这个后效性的影响。

我们发现，对于 $k_i$ 最小的那个，不管从谁哪里转移过来都不如直接杀了他最优，这启示我们通过排序来确定转移先后。

我们考虑对于 $\forall v\in R_i, v\to i$。

做一个类似 topsort 的过程，先将所有元素存入堆中，按 $k_i$ 的大小排序，然后取出堆顶 $x$，更新 $x$ 能到达的节点的答案，然后该节点的 $R$ 减 $1$。若节点的 $R=0$ 则加入堆（该节点已经更新完了），此时是将点的 $dp$ 值作为关键字排序（当然一开始以 $k_i$ 为关键字的元素仍然是让 $k_i$ 参与排序）。

注意每个点只要被访问一次，所以开一个 vis 记录一下，若被访问过了答案肯定不够优，跳过即可。

然后答案就是拓扑序最大的那几个点的 $dp$ 值。

此题考察图论算法的本质，不再是滥用模板。

~~我怎么感觉做过类似套路？？？~~

2022-07-13

[SDOI2018]旧试题

还是先莫反：

\[\sum_{i=1}^{A}\sum_{j=1}^{B}\sum_{k=1}^{C} d(ijk) \\ =\sum_{i=1}^{A}\sum_{j=1}^{B}\sum_{k=1}^{C} \sum_{x|i} \sum_{y|j} \sum_{z|k} [x\perp y][y\perp z][x\perp z] \\ =\sum_{x=1}^{A}\sum_{y=1}^{B}\sum_{z=1}^{C} \left\lfloor \frac{A}{x}\right\rfloor \sum_{u|x,u|y} \mu (u) \left\lfloor \frac{B}{y}\right\rfloor \sum_{v|y,v|z} \mu (v) \left\lfloor \frac{C}{x}\right\rfloor \sum_{w|x,w|z}\mu (w) \ \ \ \ \ \ \ \ （这里改变枚举顺序和莫反同时进行了） \\ =\sum_{u=1}^{\min (A,B)}\sum_{v=1}^{\min (B,C)}\sum_{w=1}^{\min (A,C)} \mu (u)\mu (v)\mu (w)\sum_{u|x,w|x}\left\lfloor \frac{A}{x}\right\rfloor \sum_{u|y,v|y} \left\lfloor \frac{B}{y}\right\rfloor \sum_{v|z,w|z} \left\lfloor \frac{C}{z}\right\rfloor \\ =\sum_{u=1}^{\min (A,B)}\sum_{v=1}^{\min (B,C)}\sum_{w=1}^{\min (A,C)} \mu (u)\mu (v)\mu (w)\sum_{x=1}^{\left\lfloor \frac{A}{\operatorname{lcm} (u,v)} \right\rfloor} \left\lfloor\frac{\left\lfloor \frac{A}{\operatorname{lcm} (u,v)}\right\rfloor }{x}\right\rfloor \sum_{y=1}^{\left\lfloor \frac{B}{\operatorname{lcm} (v,w)} \right\rfloor} \left\lfloor \frac{\left\lfloor\frac{B}{\operatorname{lcm} (v,w)}\right\rfloor }{y}\right\rfloor \sum_{z=1}^{\left\lfloor \frac{C}{\operatorname{lcm} (u,w)} \right\rfloor } \left\lfloor \frac{\left\lfloor\frac{C}{\operatorname{lcm} (u,w)}\right\rfloor}{z}\right\rfloor \]

我们设 $\displaystyle f(n)=\sum_{i=1}^{n}\left\lfloor\frac{n}{i}\right\rfloor$，那么就可以写成：

\[\sum_{u=1}^{\min (A,B)}\sum_{v=1}^{\min (B,C)}\sum_{w=1}^{\min (A,C)} \mu (u)\mu (v)\mu (w)f\left( \left\lfloor \frac{A}{\operatorname{lcm} (u,v)} \right\rfloor\right) f\left( \left\lfloor \frac{B}{\operatorname{lcm} (v,w)} \right\rfloor\right) f\left( \left\lfloor \frac{C}{\operatorname{lcm} (u,w)} \right\rfloor\right) \]

发现 $f$ 本质是求约数个数~~（所以你把它弄成整除分块的形式干嘛）~~，所以可以 $O(n\ln n)$ 预处理。

我们只需要考虑，如何统计这个三元组的答案。

我们考虑将数看成点，然后对于 $\operatorname{lcm} (u,v) < lim$ 的点 $u,v$ 连边，边权为 $\operatorname{lcm} (u,v)$。

这样就是三元环计数板子了，期望复杂度 $O(V+V\ln V+m\sqrt{m})$，$V$ 是值域，$m$ 是边数。

不过 $m$ 的上限可能是 $O(n^2)$ 的，并且连边过程也是 $O(n^2)$ 的，怎么优化？

首先，我们考虑将 $\mu$ 为 $0$ 的点删去，这样会少一点点数。

然后，我们枚举一个 $\gcd$，再枚举两个互质的 $i,j$，这样建边会比 $O(n^2)$ 快，但不是 $O(m)$ 的。

大佬们说这样做 $m\le 760741$，我也不知道为什么。

~~我的能力不允许我探究这么多~~

除了反演部分其它都是看题解的，最后仍是一知半解，以后少写这种过度超出自己能力范围的题v

[SNOI2019]通信

首先想个简单建模，$i^{\prime}$ 表示 $i$ 的虚点：

$S\to i,i\in [1,n]$，流量为 $1$，费用为 $0$。
$i \to T,i\in [1,n]$，流量为 $1$，费用为 $W$。
$i\to j^{\prime},j\in [1,i)$，流量为 $1$，费用为 $|a_i -a_j |$。
$i^{\prime} \to T,i\in [1,n]$，流量为 $1$，费用为 $0$。

连边是 $O(n^2)$ 的，考虑优化。

自己想的时候往线段树优化建图的方向上想，结果发现 $|a_i -a_j |$ 不好解决，然后再题解区看到了一种好一些的分治做法。

考虑分治，对于一个区间 $[l,r]$，考虑将区间内的点的权值排序去重后变成虚点，每两个相邻点之间连一条流量为 $+\infty$，费用为它们的差的边，这里要连两条（当然如果要建反图就连了四条），然后对于 $[mid+1,r]$ 的点，我们连一条出边到它的对应权值上，流量为 $1$，费用为 $0$，同样对于 $[l,mid]$ 的点，我们连入一条入边，从它的权值对应的点，流量为 $1$，费用为 $w$。

点数与分治时间复杂度同阶，边数与点数同阶，都是 $O(n\log n)$。

文理分科

最小割经典建图，对于每个点 $i$ 建两个虚点 $i^{\prime},i^{\prime\prime}$。

$S\to i$ 流量为 $art_i$。
$i\to T$ 流量为 $science_i$。
$S \to i^{\prime}$ 流量为 $same\_ art_i$。
$i^{\prime} \to V,V=\{j|j与i相邻\}\cup {i}$，流量为 $+\infty$。
$V \to i^{\prime\prime},V=\{j|j与i相邻\}\cup {i}$，流量为 $+\infty$。
$i^{\prime\prime} \to T$，流量为 $same\_ science$。

小M的作物

建模思路同上。

退役了，如果要说点什么，我就在这说了。

我一直很喜欢 OI，退役的原因和 OI 无关。
学 OI 就是没有希望我也会留着的，毕竟我做一天和尚就撞一天钟。
至于退役原因的话，当然是因为“问心无愧”的双标。
大学有机会的话我肯定会参加 ACM，不过我可能大概率回去学数学？
总之再见了，唯一靠兴趣吃饭的生活，接下来都是功利了。

想必当事人一定会看懂罢，我就不做解释了。

回想起我差不多 1 年的 OI 生涯，我学的东西也不是很多。

但它们都给我带来了我学 whk 得不到的乐趣。

即使我连省一都没有。

不过，我也算不了 OIer 罢，大概只能算一个接触过 OI 的 whker 罢，所以没有退役这一说？

反正 MO 之类的是来不及了，我肯定没机会搞。

所以只能学 whk 了，不过 MO 之流我会弄点，比如我接下来发的东西。

也是个人兴趣了。

对于暑假，我只想凭情怀做事。

分班考试什么的，随他去吧。

我仍是我，始终如一。

只是 rpdg(2020~2022) 死了。

2022-07-18

小蓝本数论习题1

1

不证自知。

显然 $1,2,\cdots ,n$ 中被 $k$ 整除的数一定是 $k,2k,\cdots ,dk$，其中 $dk\le n$ 但 $(d+1)k >n$，不难发现 $d=\left[\dfrac{n}{k}\right]$。

2

不难发现 $n^2+9n-2=(n+11)(n-2)+20$，又因为 $(n+1)|(n^2+9n-2)$，所以 $(n+11)|20$，解得 $n=9$，不难得出结论。

3

例题的套路……

$\displaystyle n-T(n)=(10+1)a_1+(100-1)a_2+\cdots +[10^k+(-1)^{k}]a_k=\sum_{i=1,2\nmid i}^{2\left[\frac{k}{2}\right]+k\bmod 2} (10^k+1)a_i + \sum_{i=2,2\mid i}^{2\left[\frac{k}{2}\right]} (10^k-1)a_i$。

右边显然是 $99,9999,\cdots$，这样的形式，必然是 $11$ 的倍数，左边保证了 $i$ 是奇数，于是 $10^i+1=(10+1)(10^{i-1}+10^{i-2}+\cdots +1)$，也是 $11$ 的倍数，故 $11|(n-T(n))$。

4

考虑这样一个形式：$\displaystyle n\mid \frac{\displaystyle \prod\limits_{i=1}^{n} a_i}{a_i}-a_{i}$。

所以有 $\displaystyle n\mid \frac{\displaystyle \prod\limits_{i=1}^{n} a_i -a_i^2}{a_i}$。

于是 $\displaystyle n\mid \displaystyle \prod\limits_{i=1}^{n} a_i -a_i^2$。

把所有 $i$ 加起来，可得 $n\mid n\displaystyle \prod\limits_{i=1}^{n} a_i - \sum_{i=1}^{n}a_i^2$。

$n\displaystyle \prod\limits_{i=1}^{n} a_i$ 显然被 $n$ 整除，由整除的性质可得 $\displaystyle n\mid \sum_{i=1}^{n}a_i^2$。

5

假设命题成立。

那么 $(ad-bc)\mid a,(ad-bc)\mid d$，所以 $(ad-bc)^2\mid ad$。

同理 $(ad-bc)^2\mid bc$，所以有 $(ad-bc)^2\mid (ad-bc)$，与 $ad-bc>1$ 矛盾，故命题不成立。

6

考虑到 $b-k \mid b^n-k^n$，所以 $b-k\mid |a-b^n|$，考虑到 $k$ 是任意整数（其它数都是给定的），所以只能有 $|a-b^n|=0$，即 $a=b^n$。

7

考虑到设 $k_i = q_im+r_i,0<r_i<m$。

那么我们有 $2^{k_i}=2^{q_im}*2^{r_i}=(2^{q_im}-1)2^{r_i}+2^{r_i}$。

显然原式可以被拆成两个部分：$\displaystyle\sum_{i=1}^{n} (2^{q_im}-1)2^{r_i}+\sum_{i=1}^{n}2^{r_i}$。

显然 $2^{m}-1\mid 2^{q_im}-1$，于是左边被 $2^m -1 $ 整除，我们考虑右边。

不妨设这个 $n$ 就是最小能满足条件的 $n$，那我们可以假设 $r_i$ 都是不重复的，毕竟有重复的可以合并掉。

那么 $\displaystyle 2^{m}-1=\sum_{i=0}^{m-1}2^{i} \mid \sum_{i=1}^{n}2^{r_i}$，所以 $\displaystyle \sum_{i=1}^{n}2^{r_i} \ge \sum_{i=0}^{m-1}2^{i}$。

由 $r_i < m$，且 $r_i$ 不重复，可知 $n\ge m$。

posted @ 2022-06-28 00:46 redproblemdog 阅读(69) 评论(0) 编辑收藏举报

刷新页面返回顶部

Izmail's home