2022摸鱼实录
AFO 的 whker 了
所以刷水题来获得快感。
2022/2/8
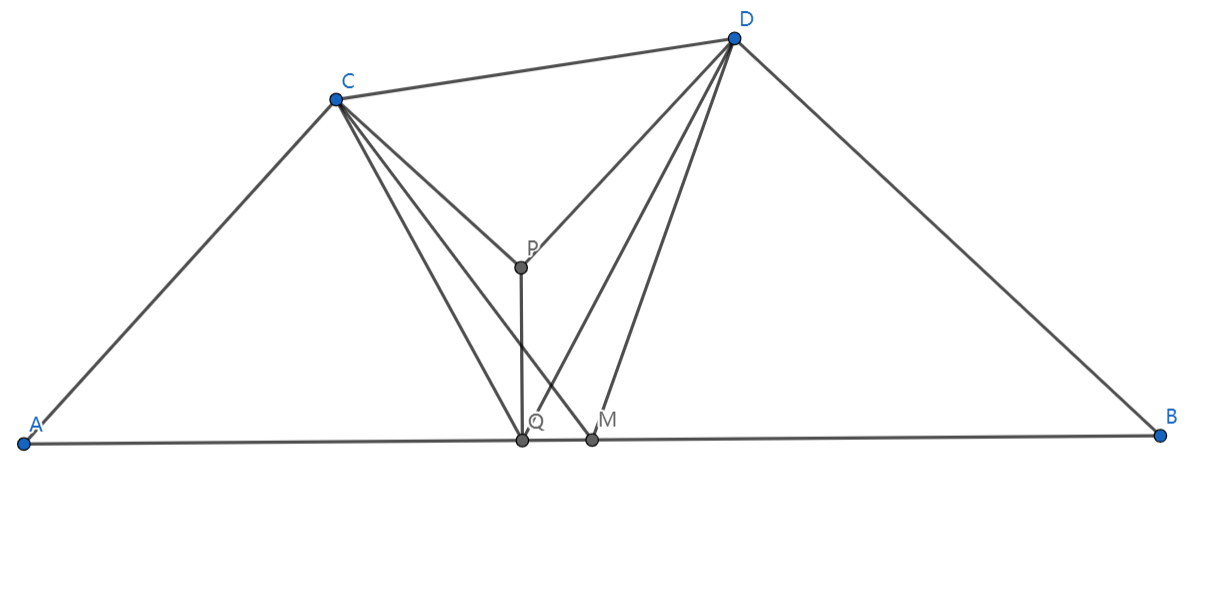
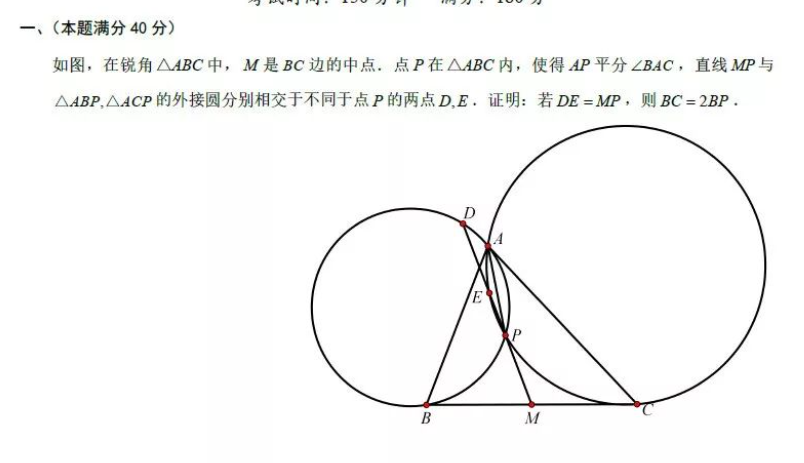
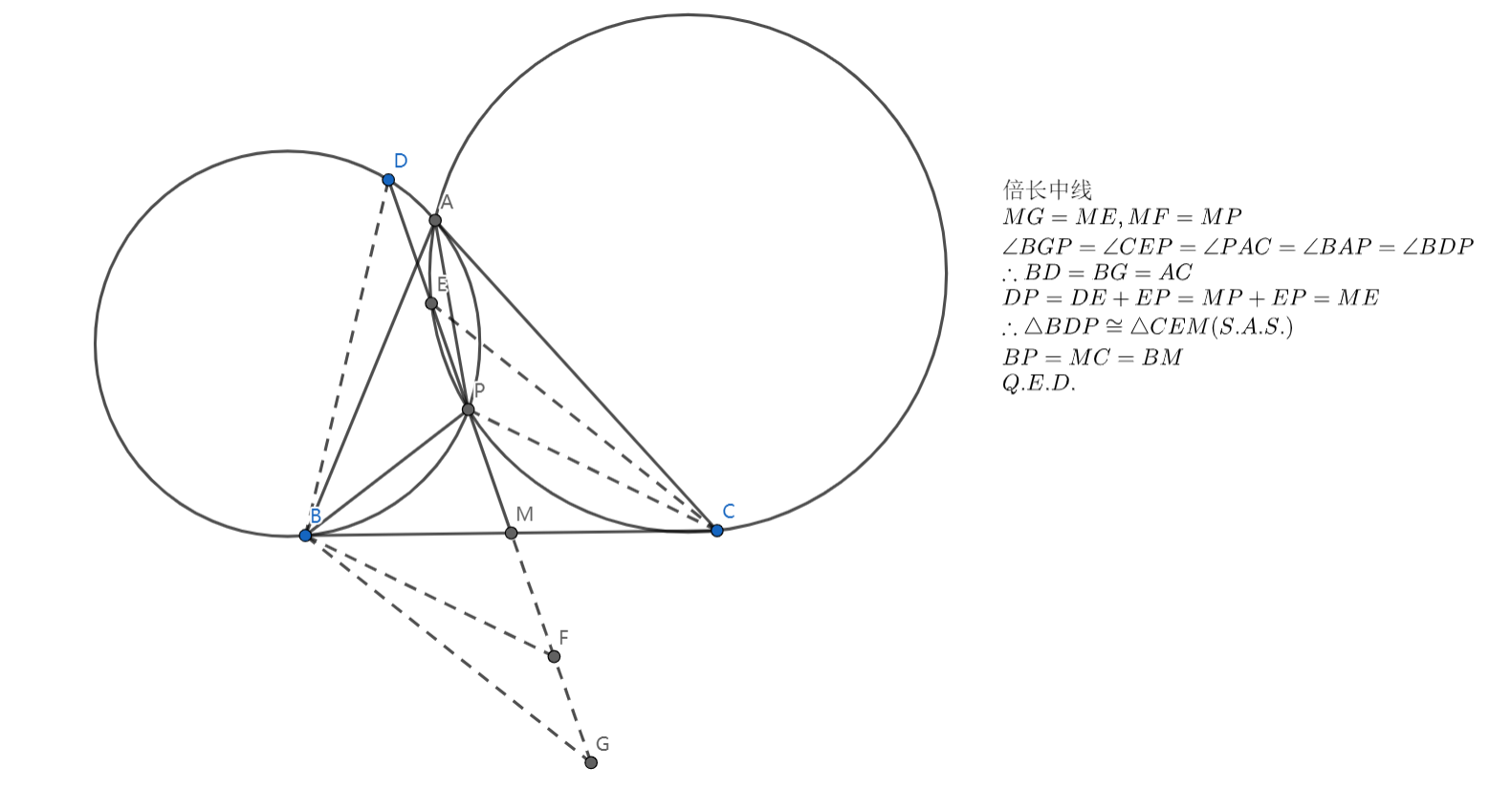
如图,,求证:
思考:不难发现有两组四点共圆: 和 ,可以考虑将圆做出来,圆心分别是 的中点,然后 又是中点,这促使我们构造中位线。
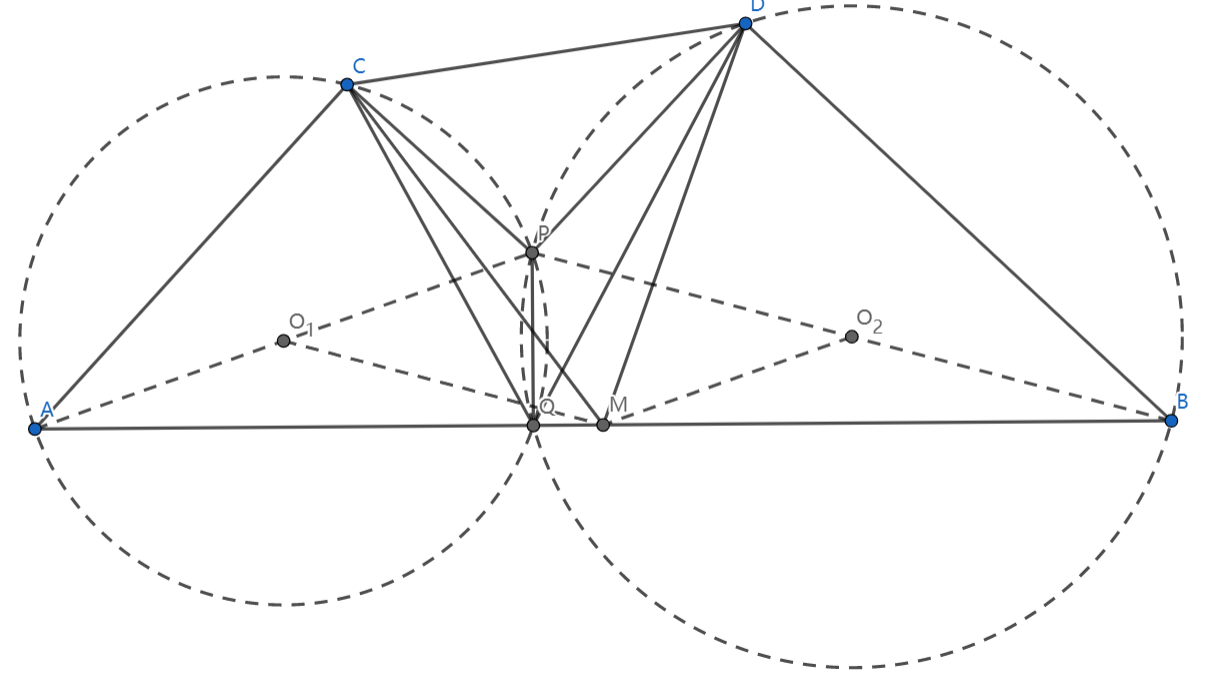
我们发现 ,这驱使我们把半径做出来:
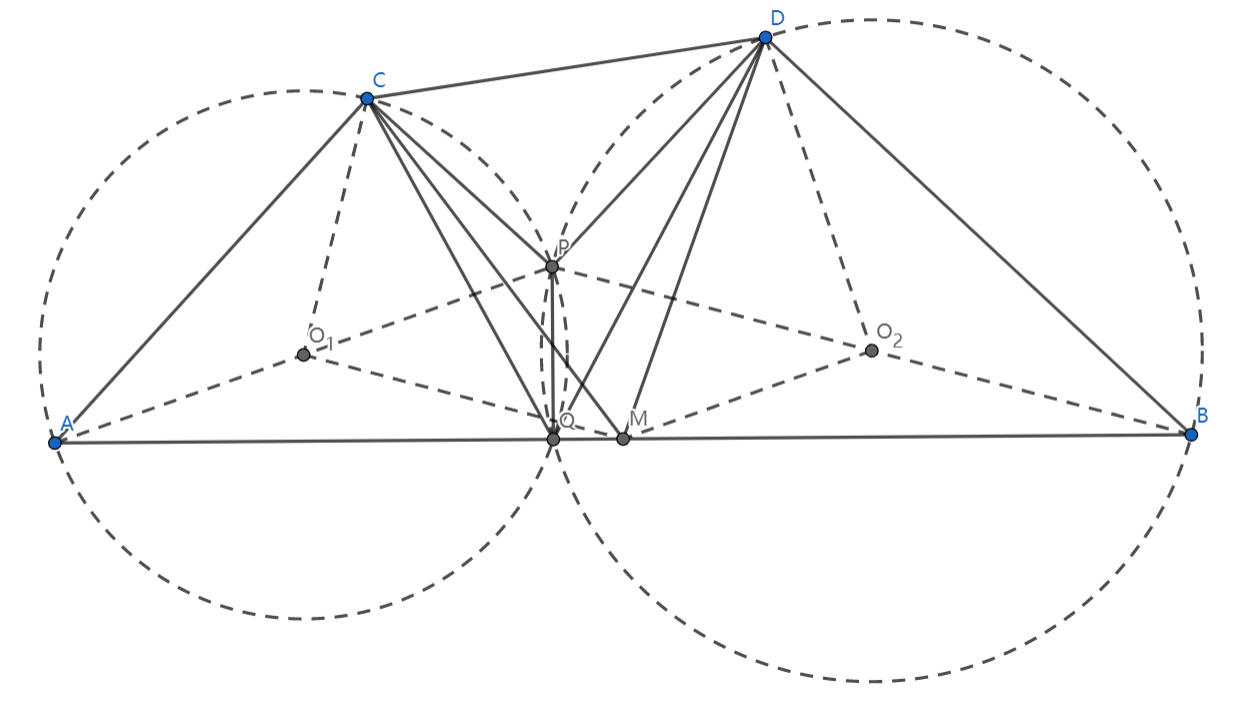
然后就可以得到一组全等三角形:,这时得到 ,因为四边形 是平行四边形(两组对边分别平行),所以 ,所以 ,所以 (同弧所对圆周角相等)。
总的来说,这题还是不错的,至少对于我这样一位中考生来说(然而这好像是 MO 题?),对我的几何能力有很大挑战,不过还是想嘲讽一下就这
2022/2/9
第一问:
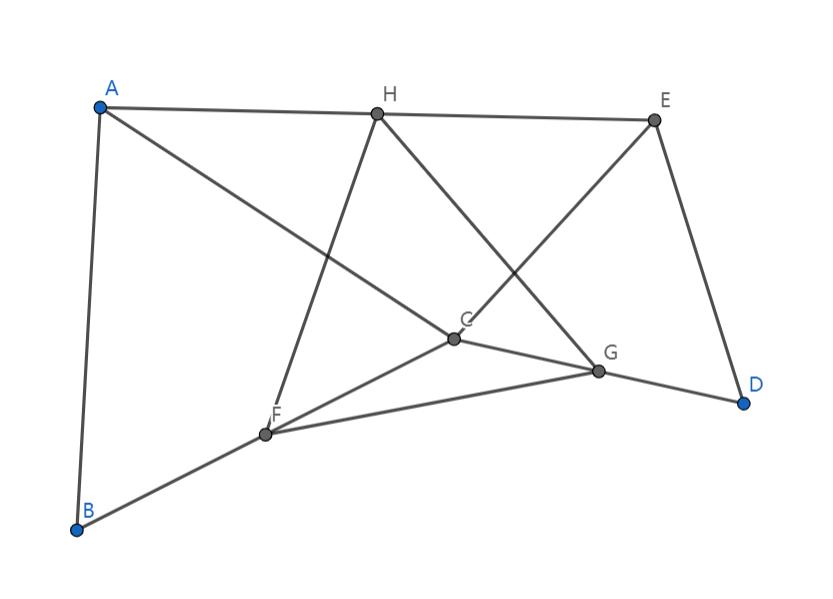
如图, 都是等边三角形, 分别是 的中点, 是 的中点,求证: 为等边三角形
看到要我们证是等边三角形,先考虑能不能转一转,似乎能把 绕 往上转,那我们考虑能不能在右上方构造一个全等于 的三角形
考虑找到 中点 ,连接 ,如图:
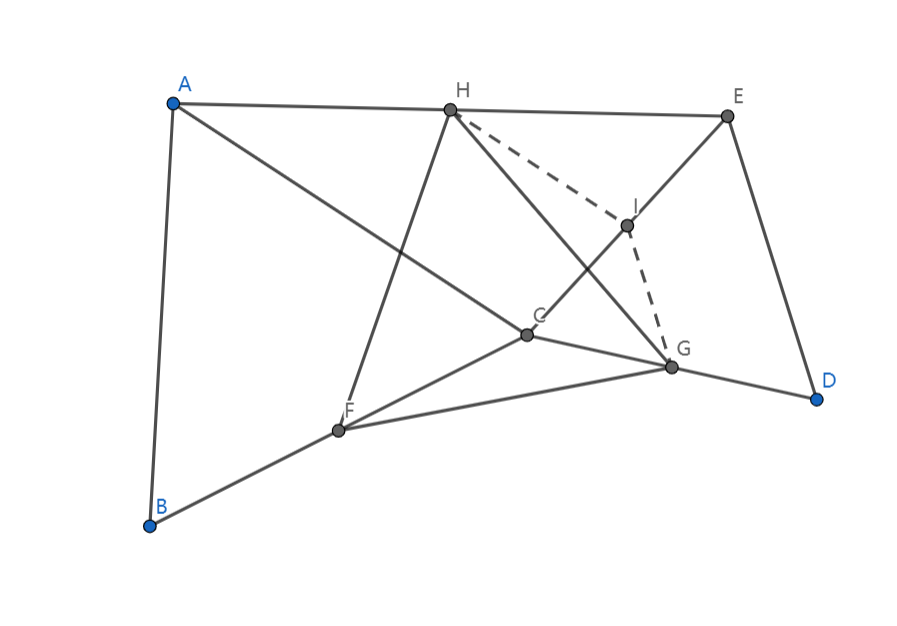
这时我们发现 (中位线),然后我们试图证明 ,这样就相当于将 绕点 旋转了。
因为 所以旋转角肯定是 ,所以我们只要证明上述角相等,命题就得证了。
那么怎么证明角相等呢?
设 ,则 ,则 ,所以 ,然后就可以证全等了。
第二问:
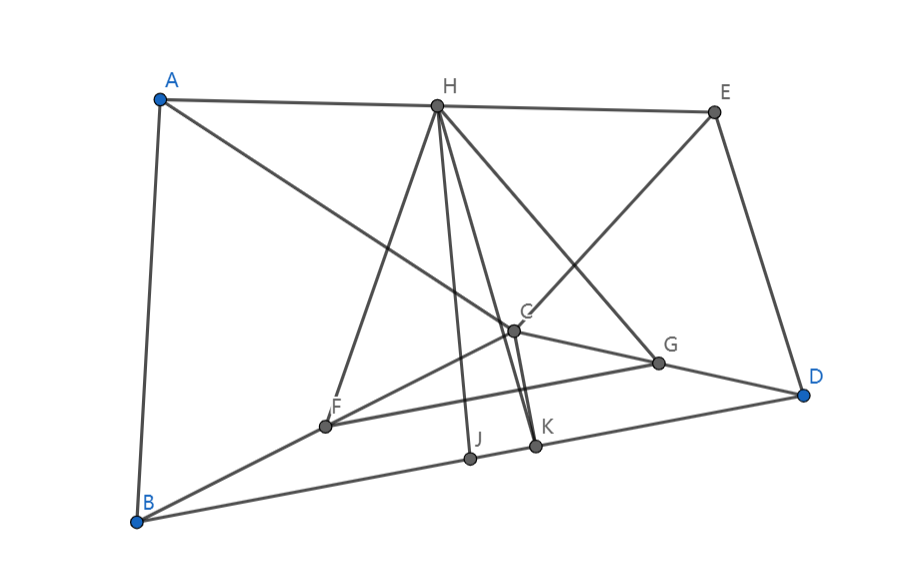
如图,在第一问的条件下, 为 中点, 于 ,求证:
我们发现 是中位线,所以 ,同时 是直角三角形斜边上的中线,所以 ,所以 。
连接 如图:
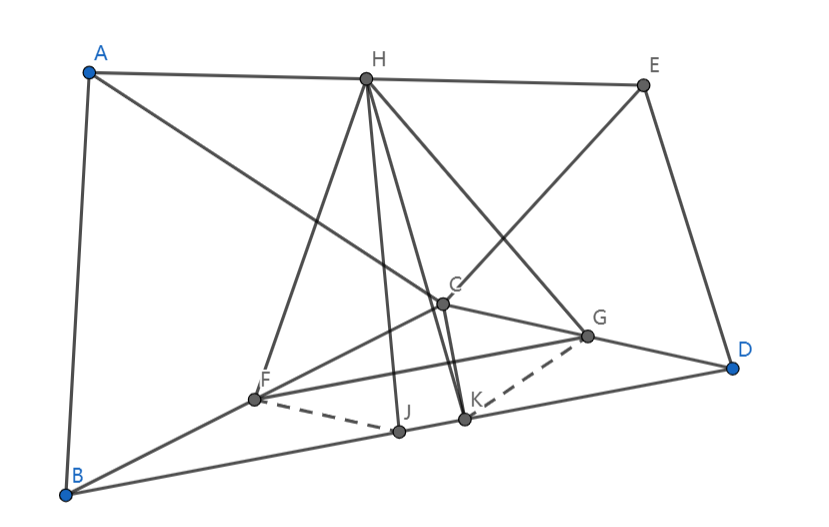
因为 ,这仍然驱使我们去证全等,考虑到 ,而 ,所以 ,又因为 ,则 ,因为 (内错角相等),所以 ,所以 ,一个 的全等就证出来了(),然后就得到 。
偶尔做做八年级的题也不错。
蛤?要分班考?
还要我准备是吧?
那我来准备力!
2022-08-09
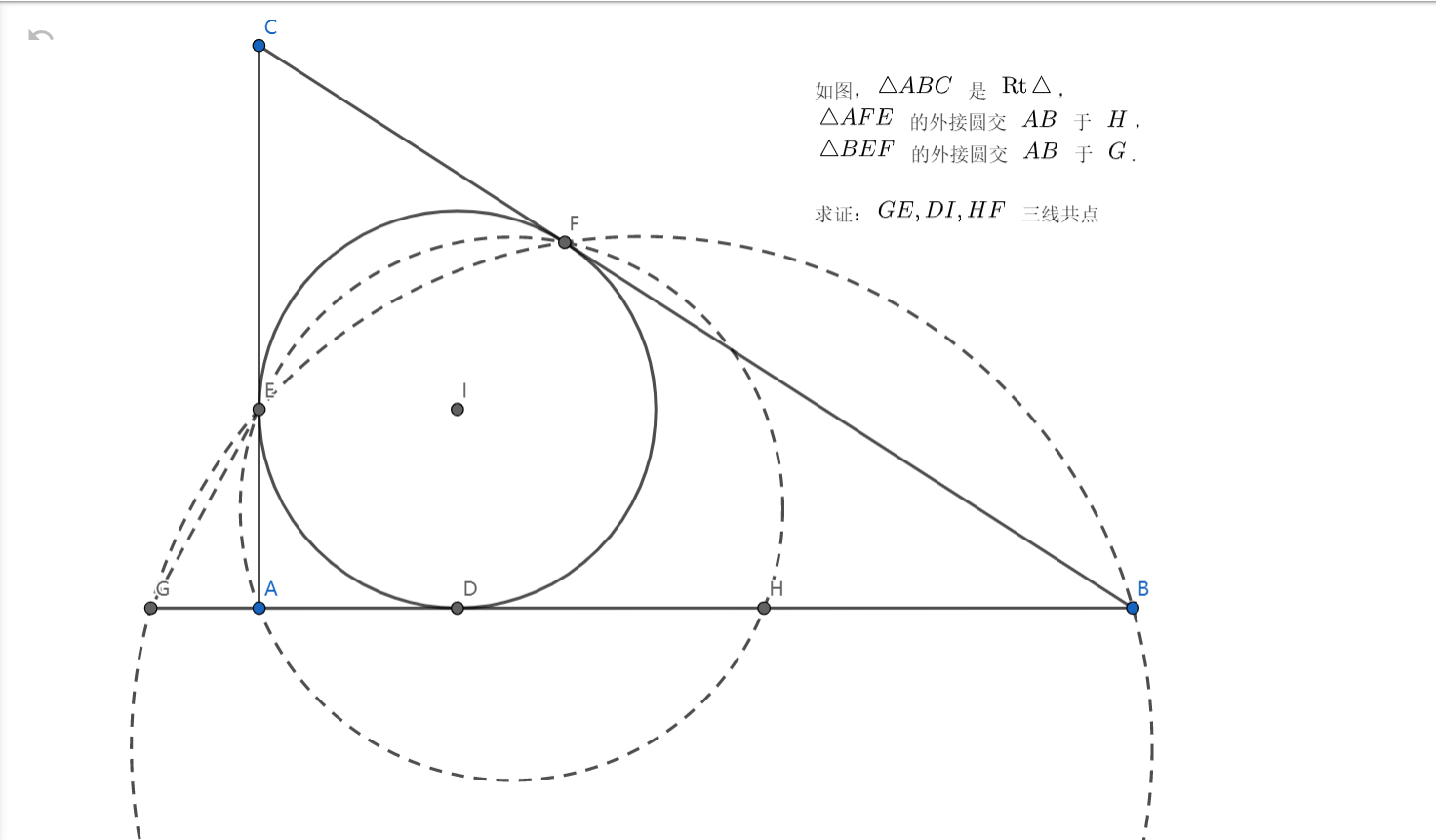
过程:
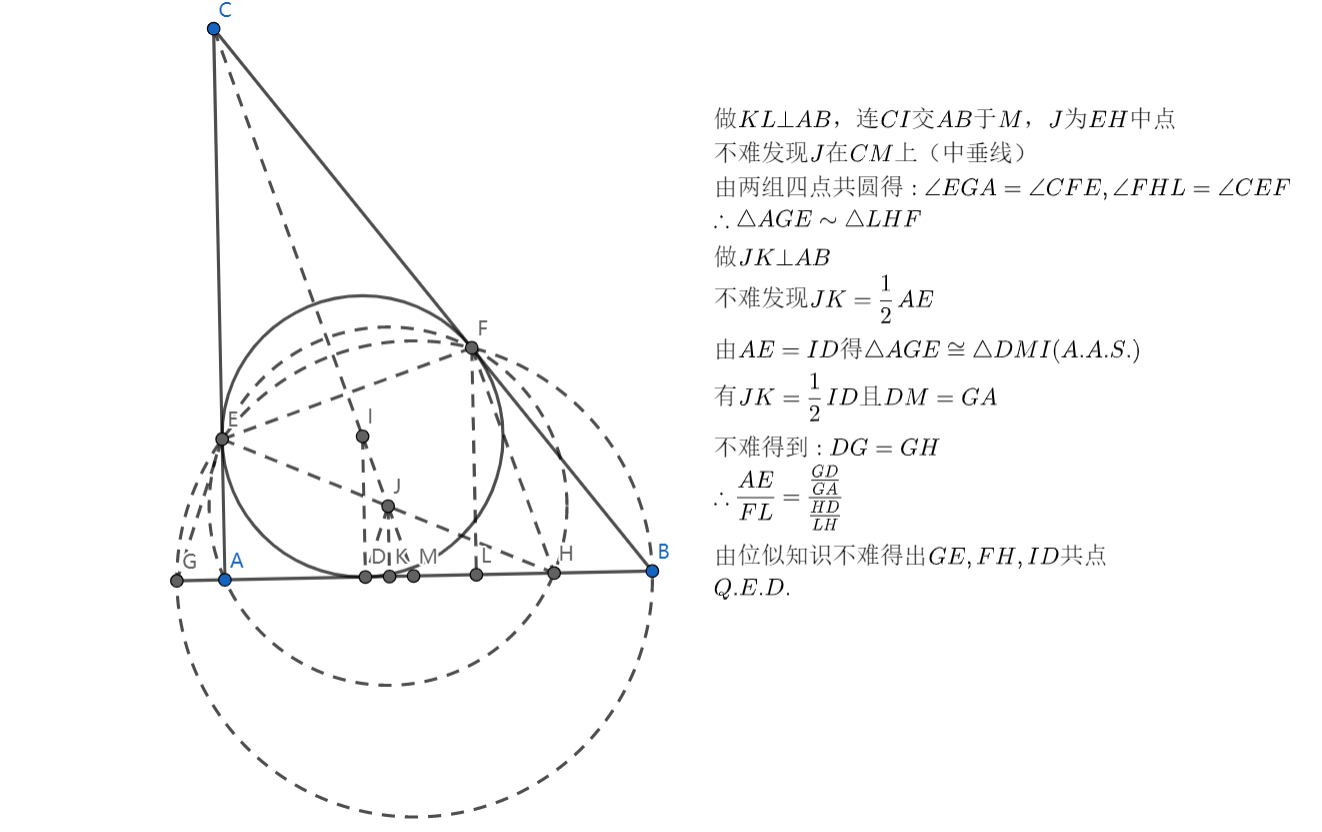
思路及评价:考虑通过相似把证共点改为线段的比例关系,原问题转换为证 为 中点,再注意到 再 上,其他就很简单了。果然是初联水题!
PS:之前以为 , 共点(lyk和ym)。
2022-08-10
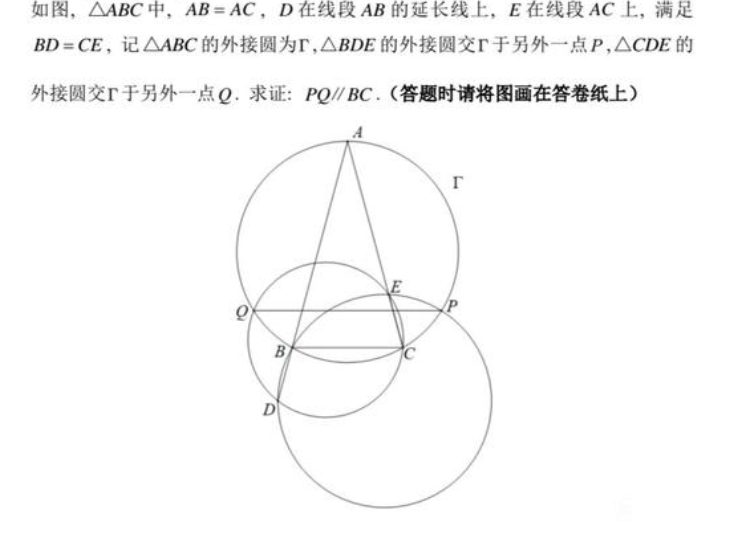
过程:
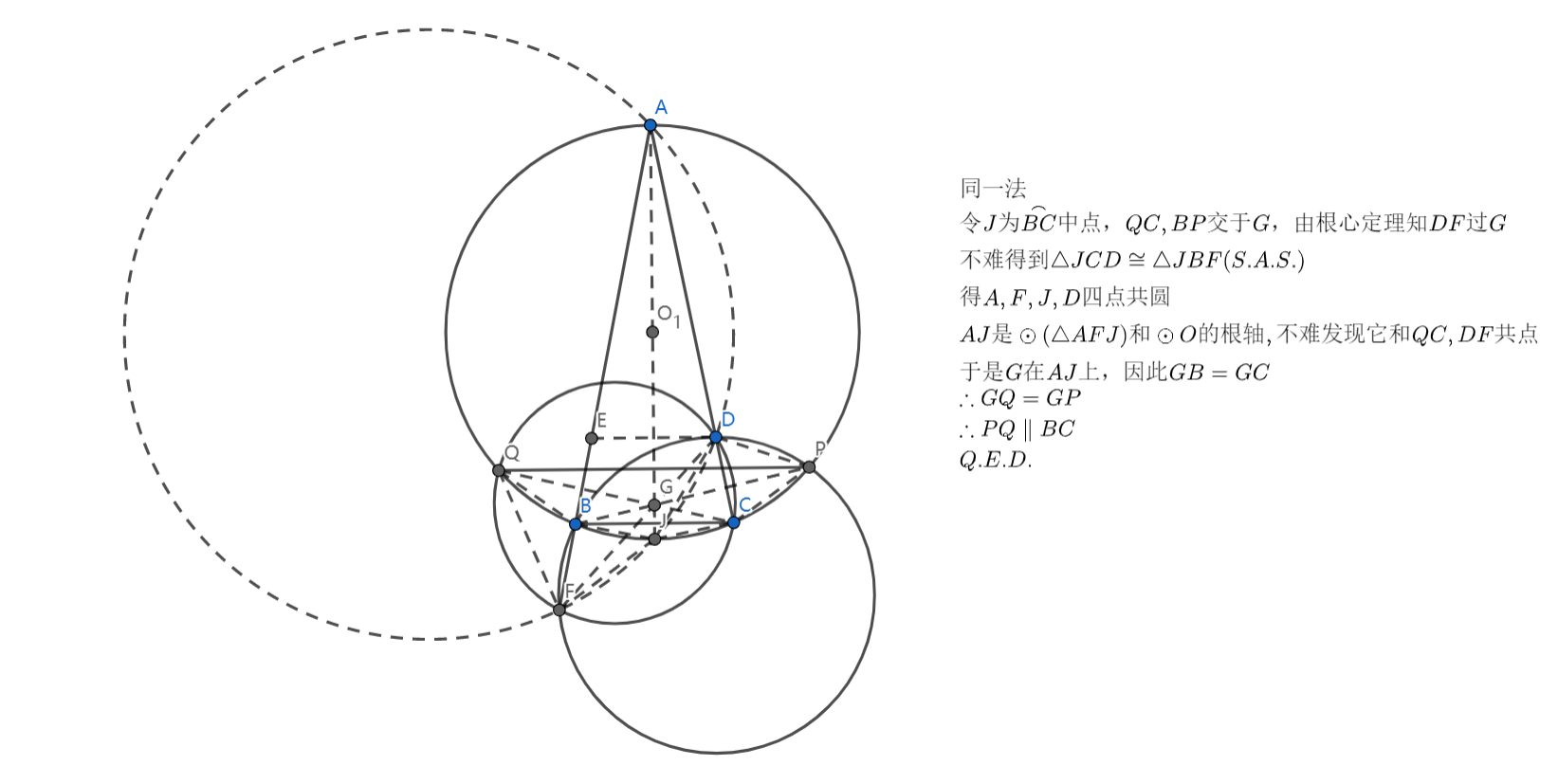
思路及评价:想到同一法就秒了(可惜我没想到,看来我还是逊),听说答案解法很难算?我觉得那些算的方法和根轴是等价的吧!这种水题少做。
2022-08-11
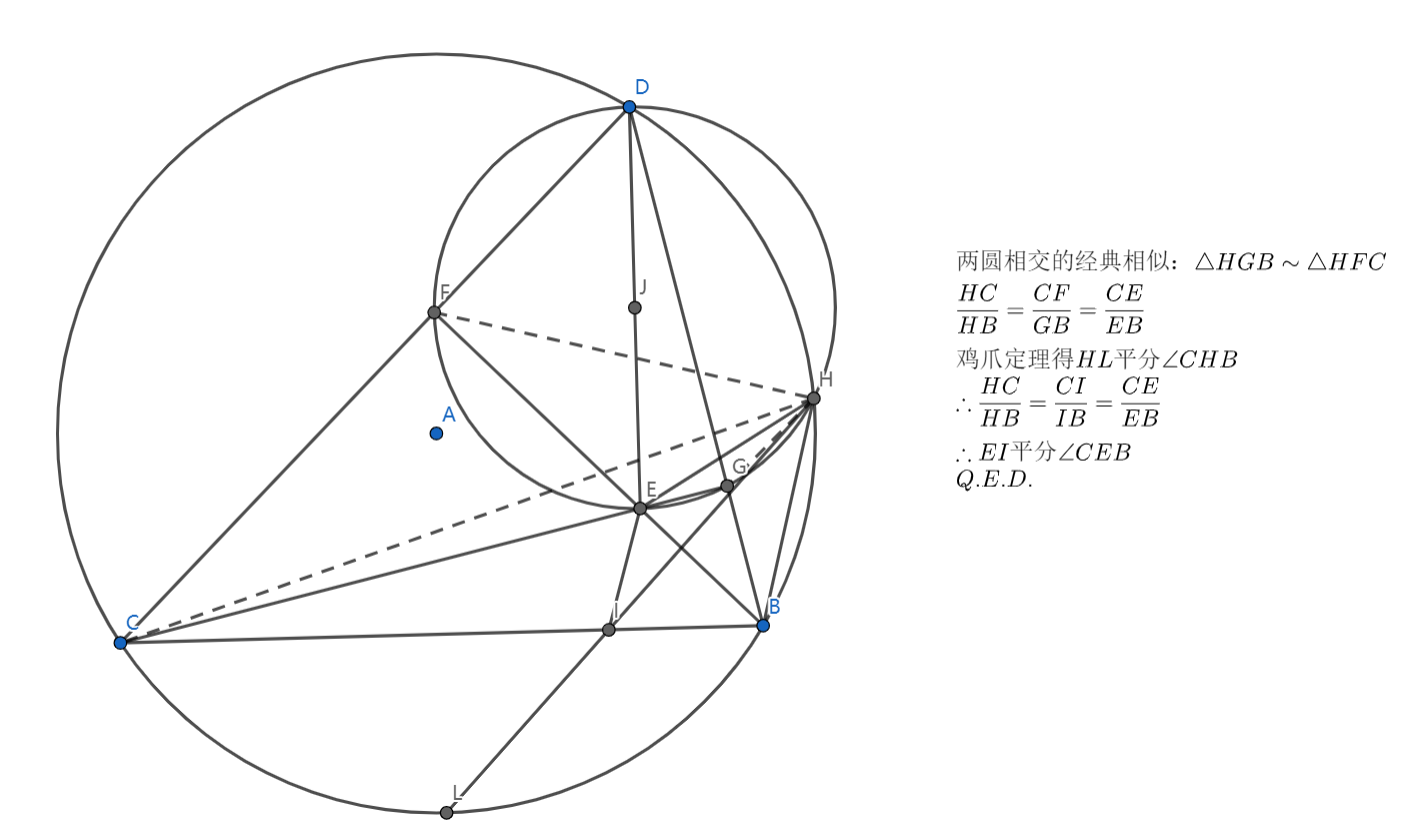
两圆相交的相似。
十分经典,于是直接放过程了。
好像还鸽了个也很简单的,不过相似比我一直导不出来。
2022-08-12
过程:
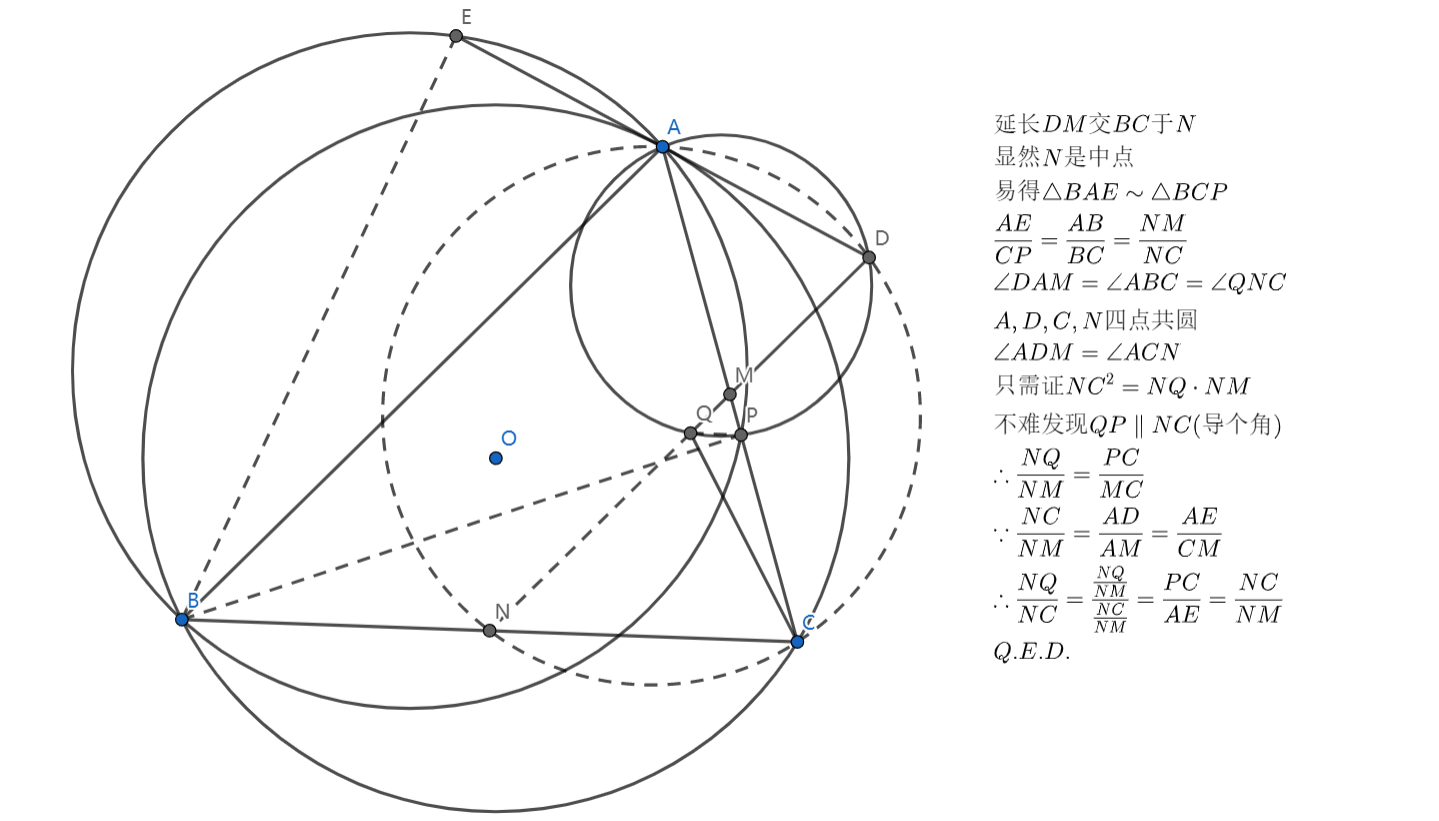
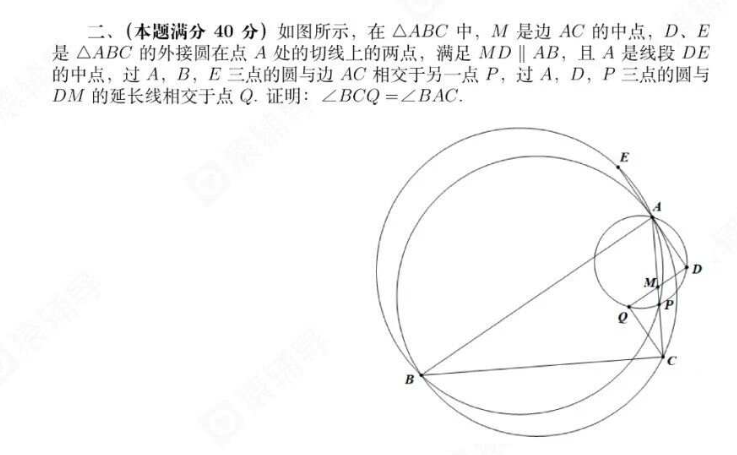
思路及评价:看到中点有很多种处理方法,中点遇上平行构造中位线,又是两圆相交的一个相似,有这些后导导角就做出来了。去年联赛题,虽然我在场外觉得很水,不过场上这个图就贼难画,而且紧张的话说不定导不出比。不过思维含量的确不高。
2022-08-13
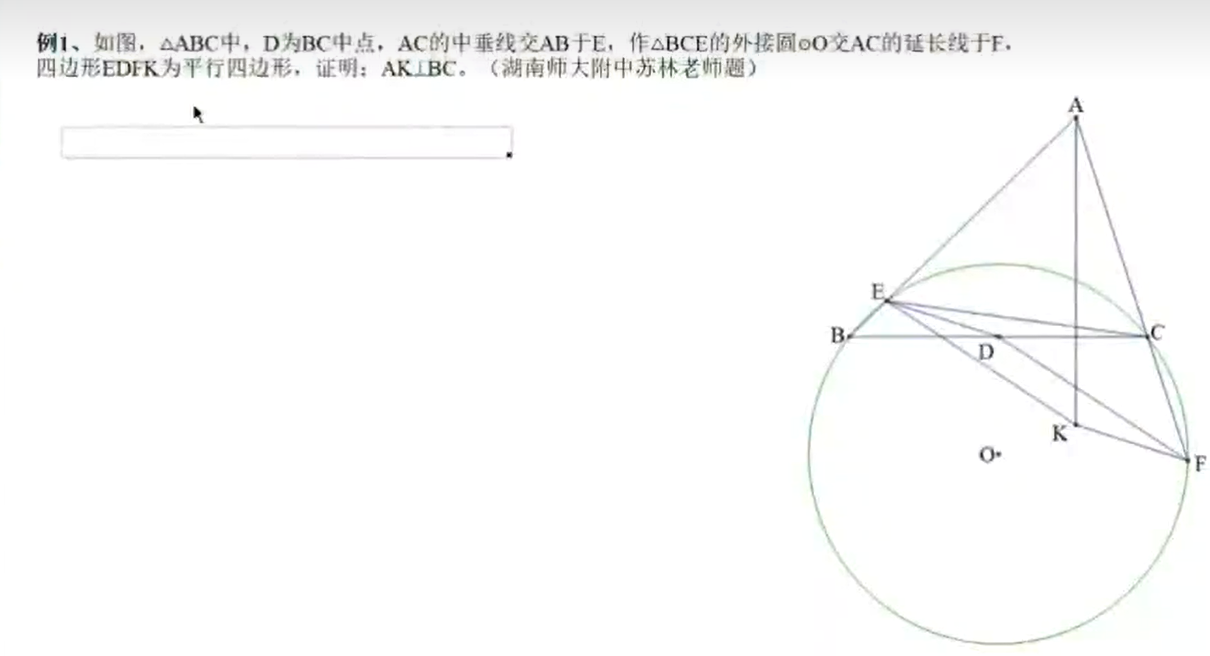
过程:
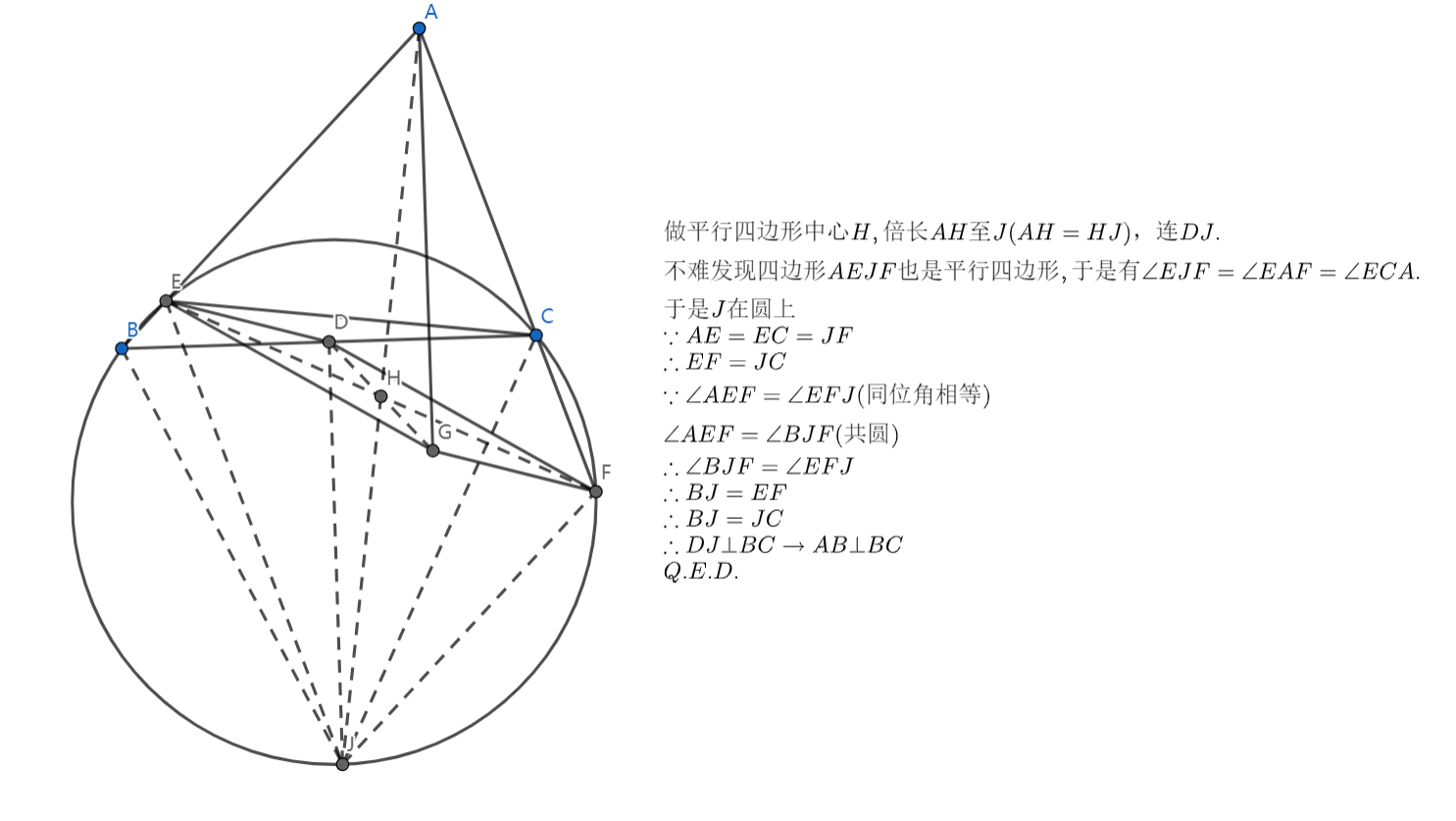
思路及评价:这里考虑把 往外移,发现平行四边形的中心也能产生中点,于是我们打算倍长,这样相当于把 移到了 上,和中点这个条件凑到一起了。然后又发现还有一个平行四边形,且发现 好像在圆上的样子,于是我们考虑先证明 在圆上,这样可以把垂直转为证边的相等,简化了问题。证完这个之后我们又发现两个等腰梯形,于是原命题的证。
很妙,我觉得。出题人通过平行四边形,等腰三角形,和圆构造出了两个等腰梯形,比较腻害!
2022-08-14
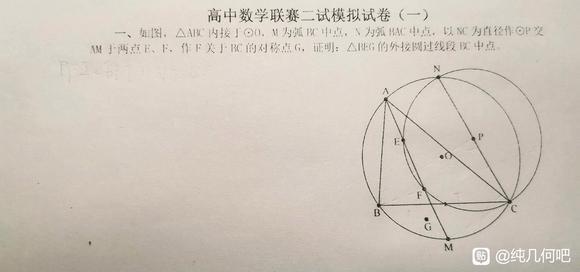
过程:
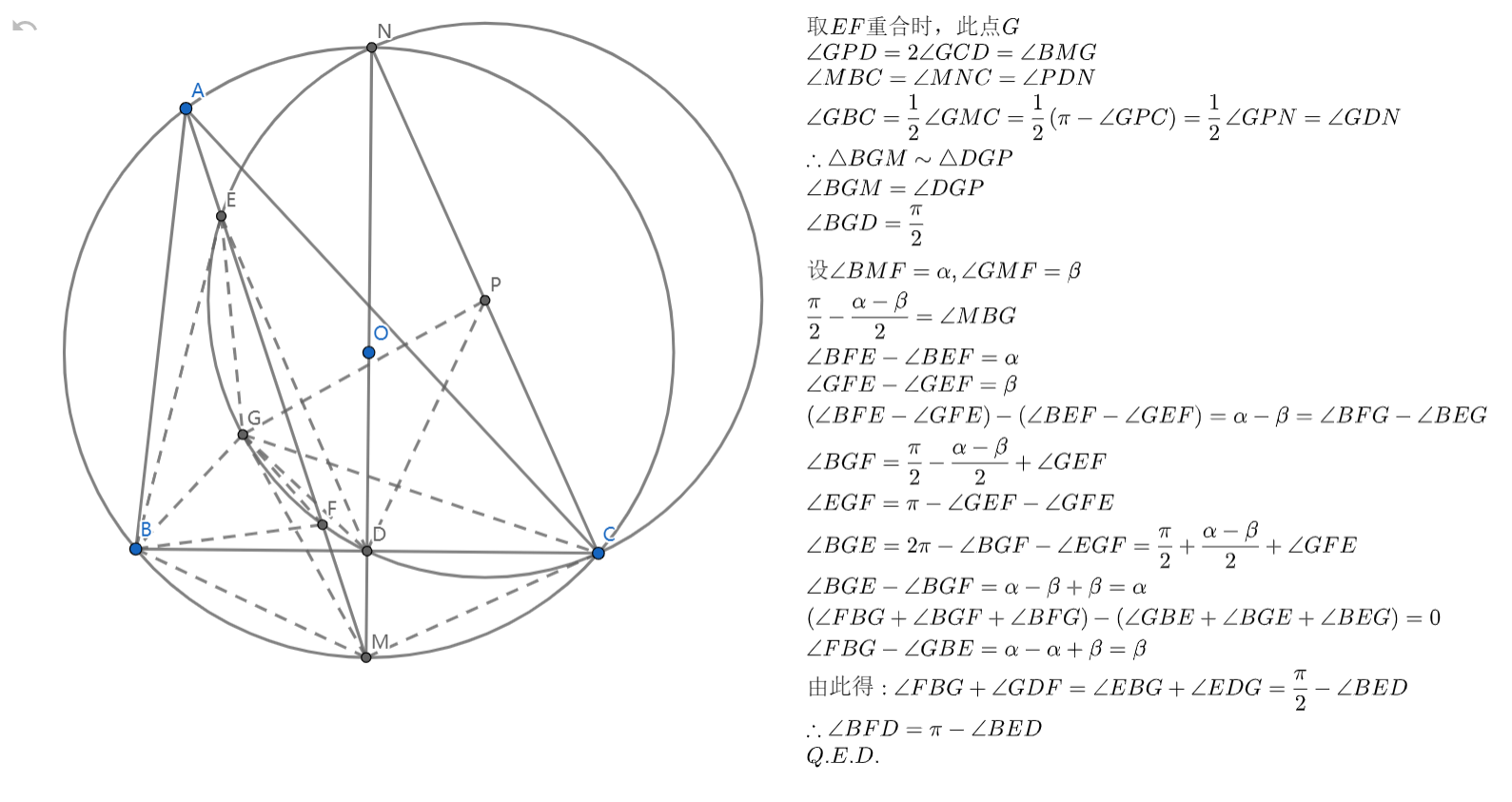
思路及评价:我的想法是,由特殊到一般,于是我先找了切点的情况,很快发现一组相似,然后证明了 ,入一般之后就是证 。下午发现 和 (其实 那个是早上发现的,下午类推),然后就考虑通过角的差值证明它们和相等,导会角就出来了。
感觉自己确实整复杂了,但是,我觉得我的思路很自然啊?
2022-08-15
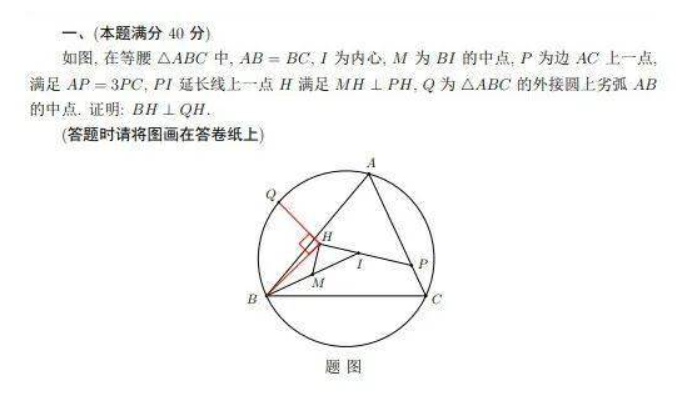
过程:
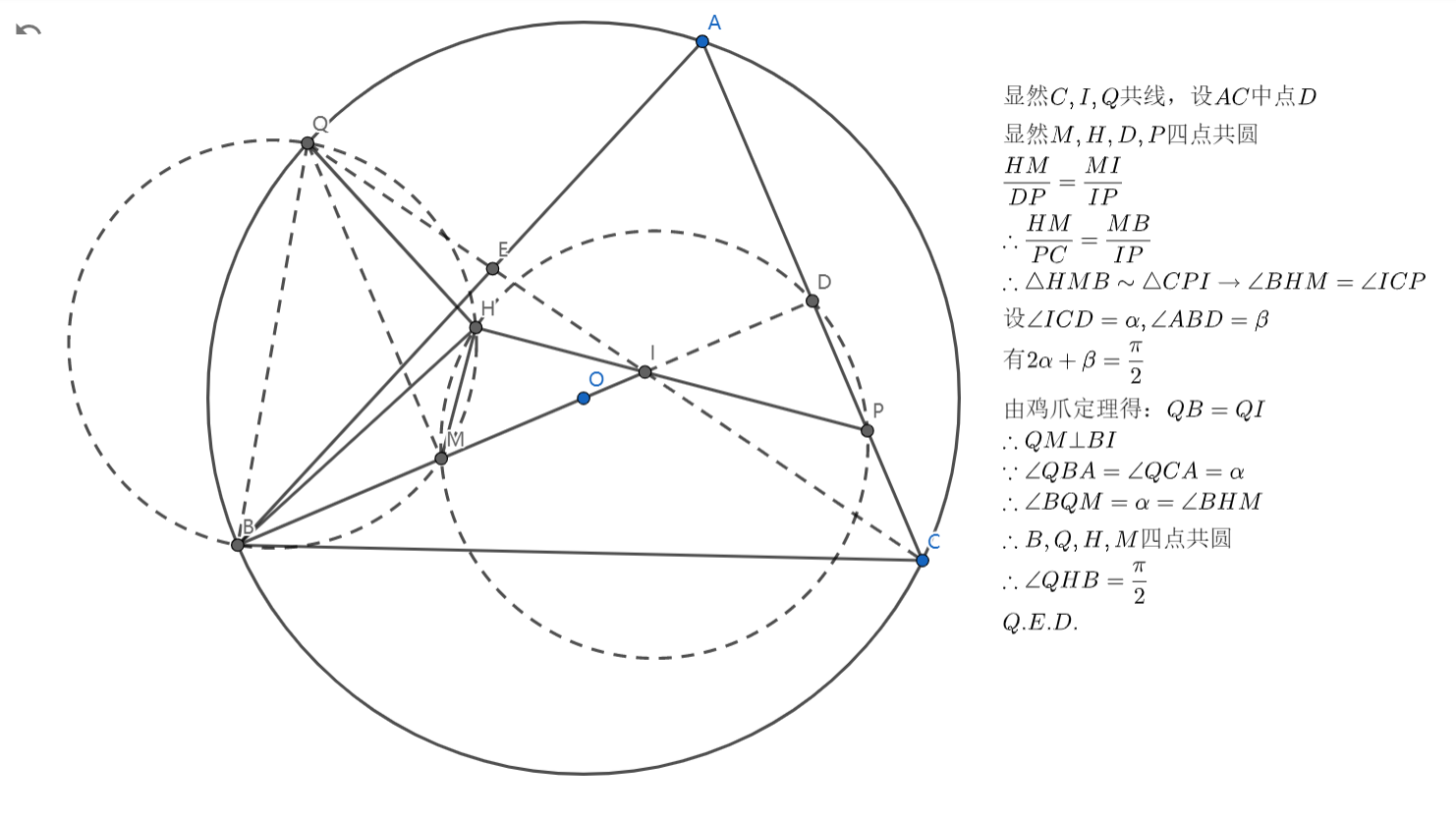
思路及评价:看到内心直觉鸡爪(因为我不会其它的了),然后发现 是四等分点,画图的时候我们会用到中点,而这个中点由于是等腰三角形的缘故会在 线上,然后 ,显然有一个四点共圆的相似,然后导导比,发现一个新的相似,然后观察到 ,考虑能不能通过四点共圆来证垂直,于是导导角,然后就出来了。
好寄吧水啊,高联几何能不能别这么水!!!这还比不上中考题趴!!!
2022-08-16
过程:
思路及评价:好几把水啊,画图竟然比做出来还难。
回学校力!听说学数竞还得选拔,我搞寄吧,我这种下三滥水平怎么打得过衡八学子……继续摸鱼。
2022-09-11
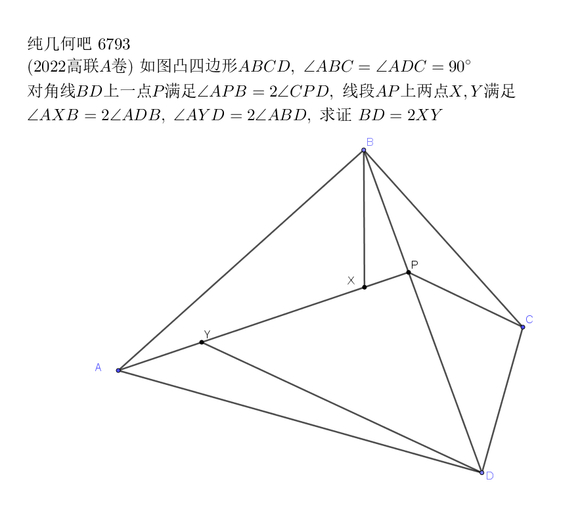
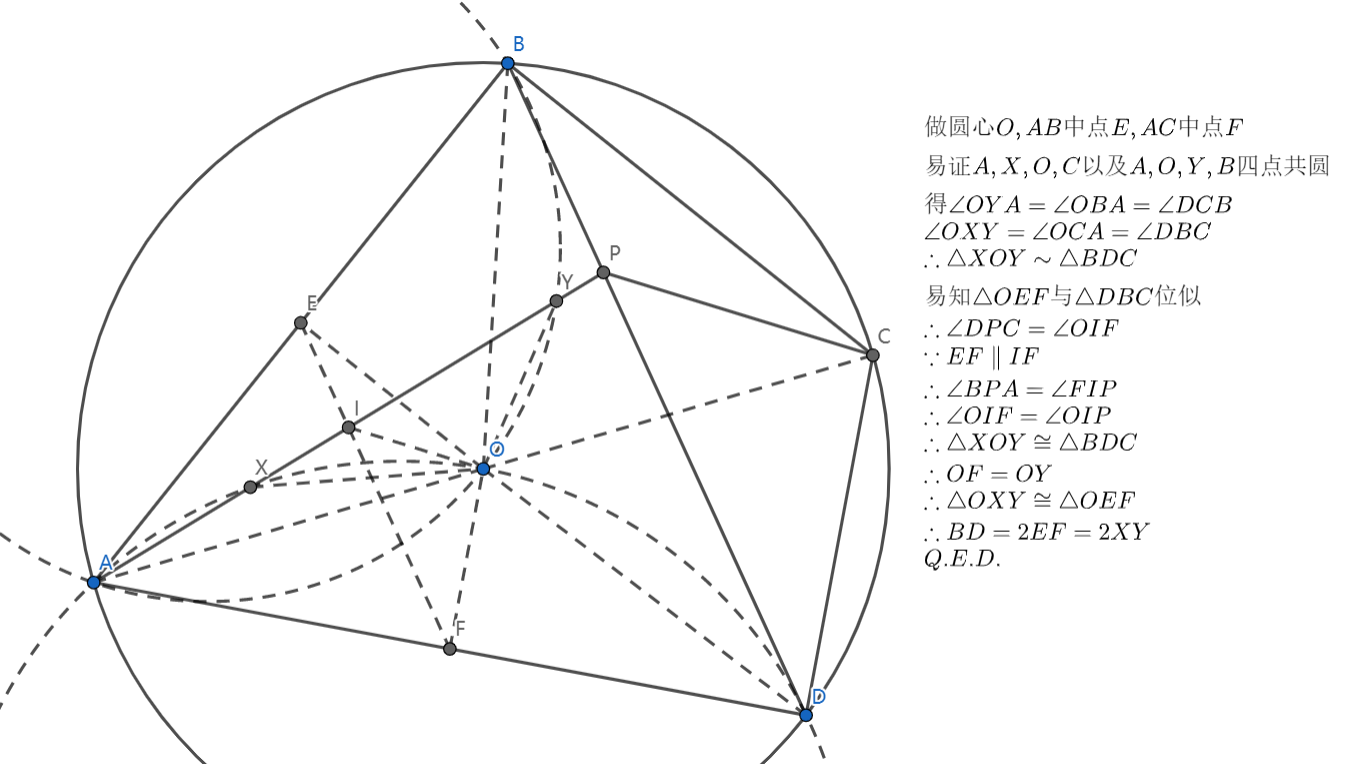
联赛脑瘫题,不做评价。
PS:xxh 初中同学 ,恐怖如斯!!!
2022-09-13
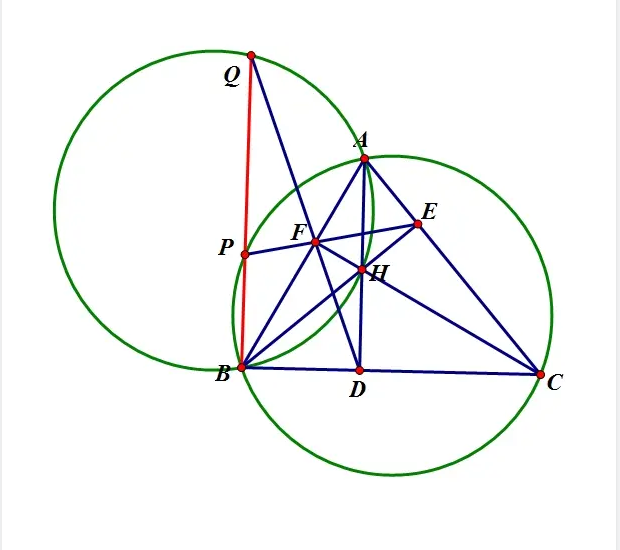
主要是注意到对称性,以及原问题等价于证明 。
疮性班作业真的好多好多好多,于是只摸了一道高联难度的水题。
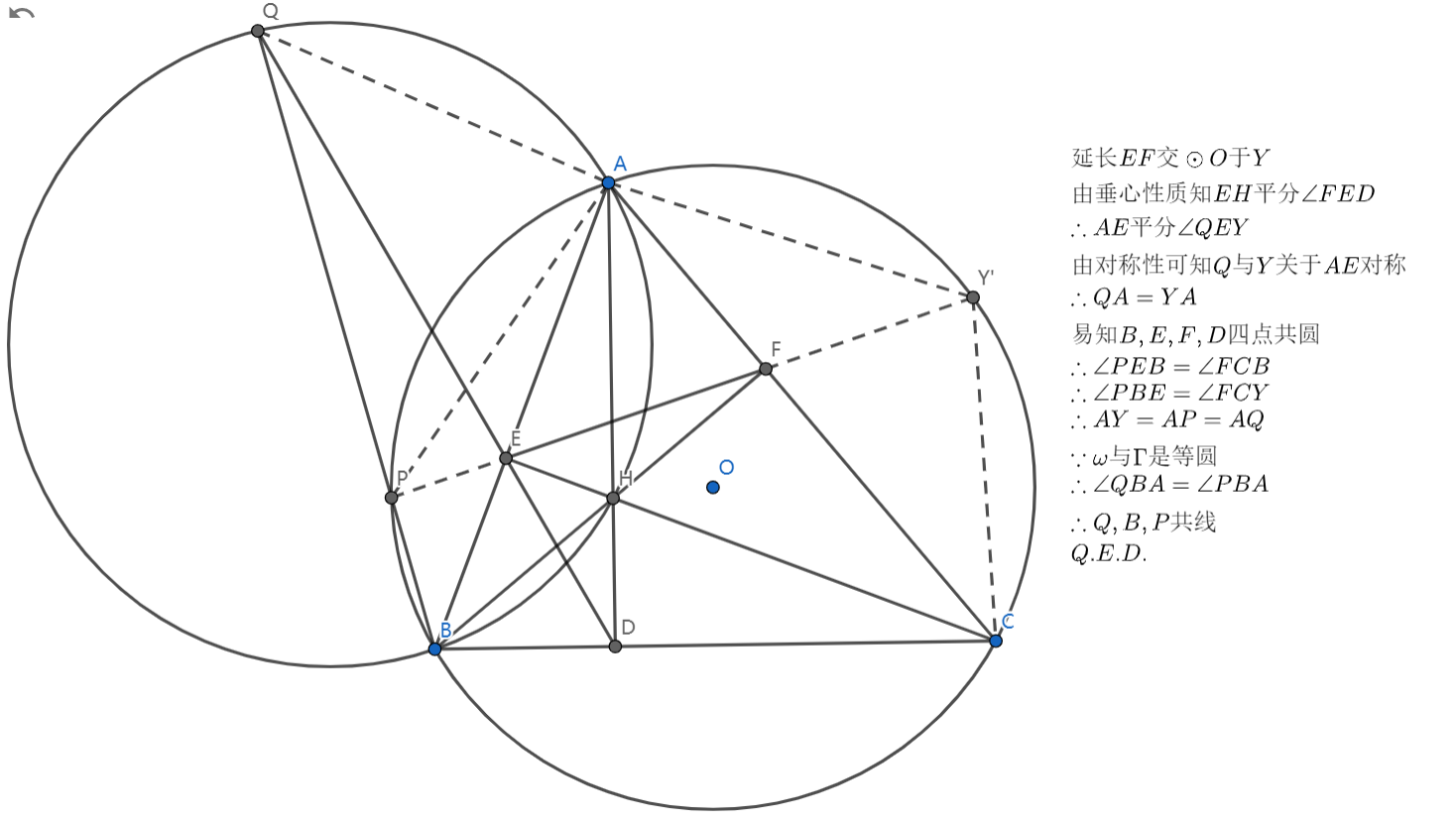
稍微改了改,准备去诈骗同学:
垂心 , 交 于 , 交 于 ,求证: 四点共圆。
2022-09-16
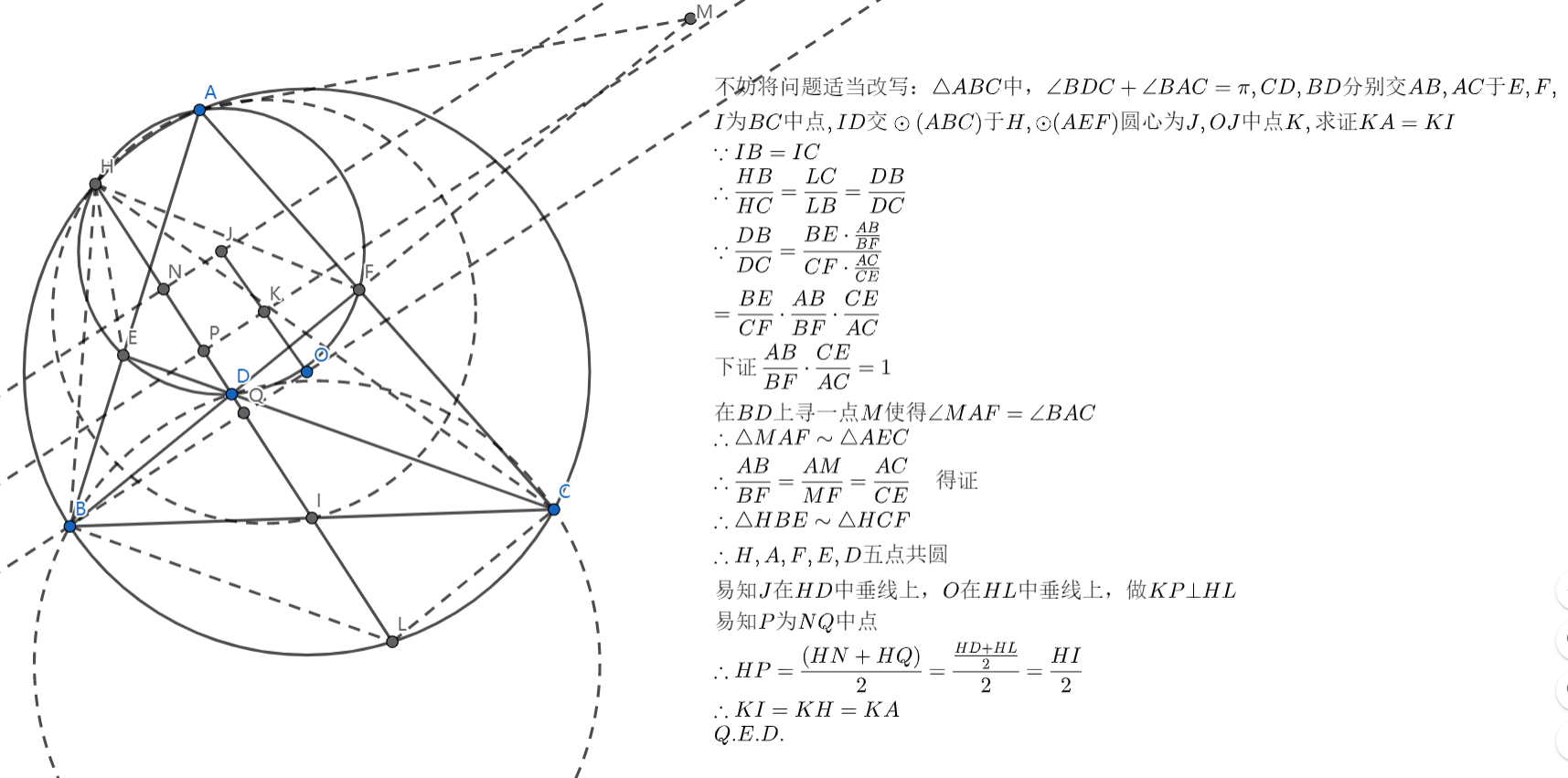
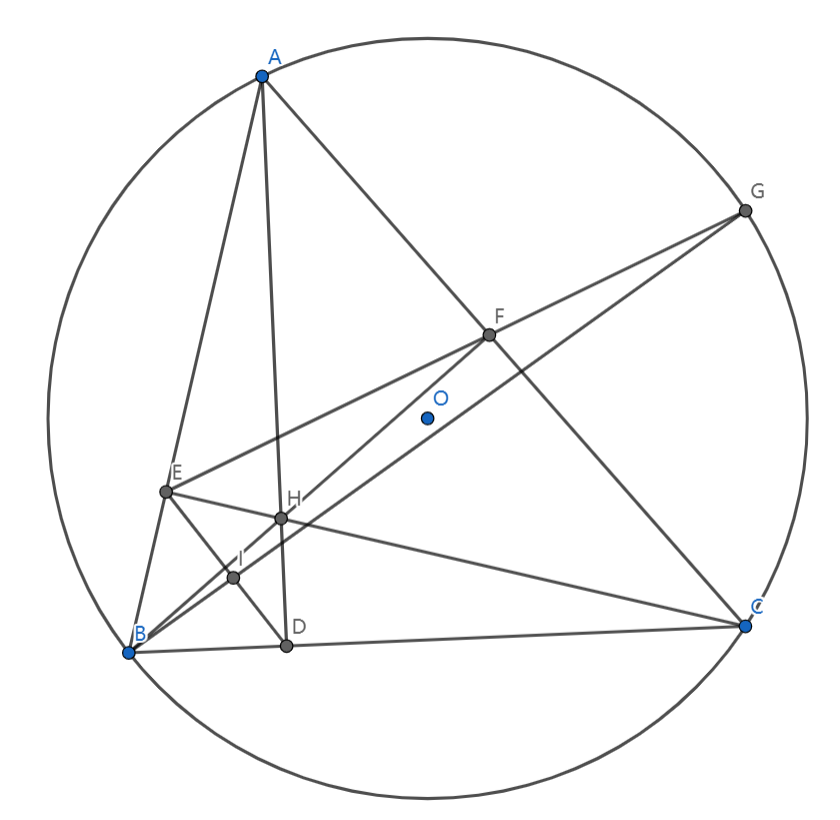
先猜后证的思想。先想到 是中点,然后转化问题去证明,之后要想到中点与中点之间的联系。
也是联赛难度水题。
2022-10-03
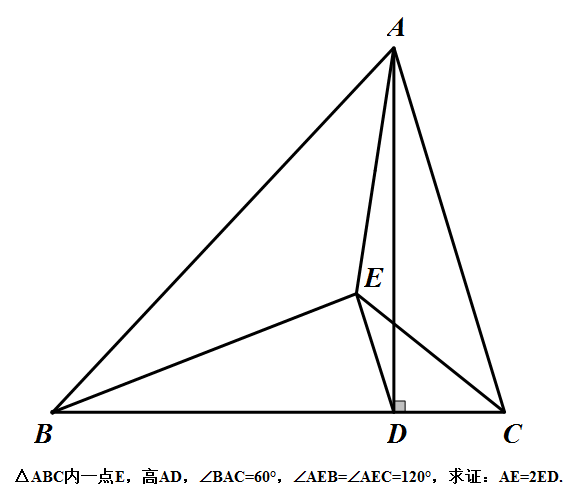
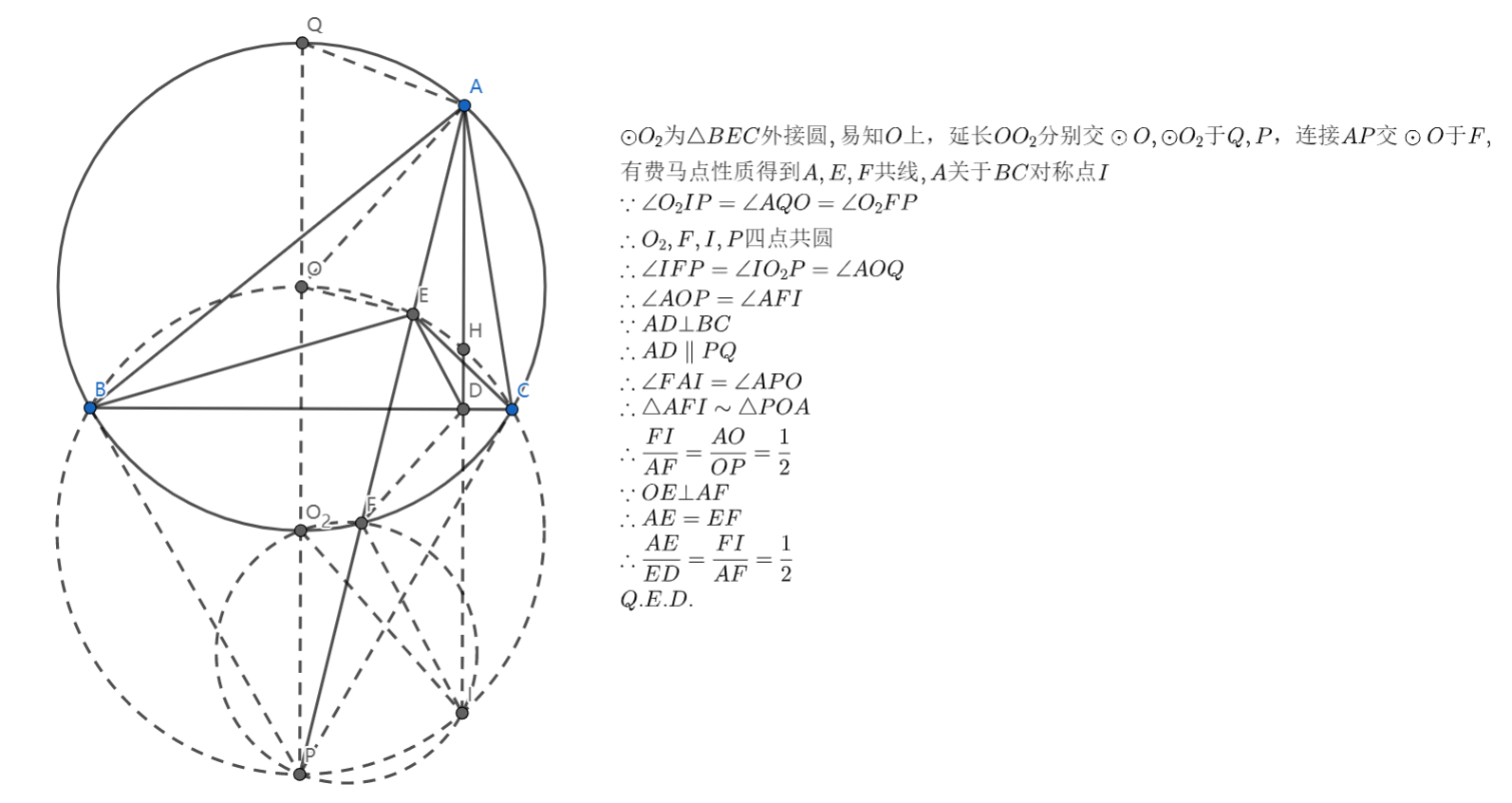
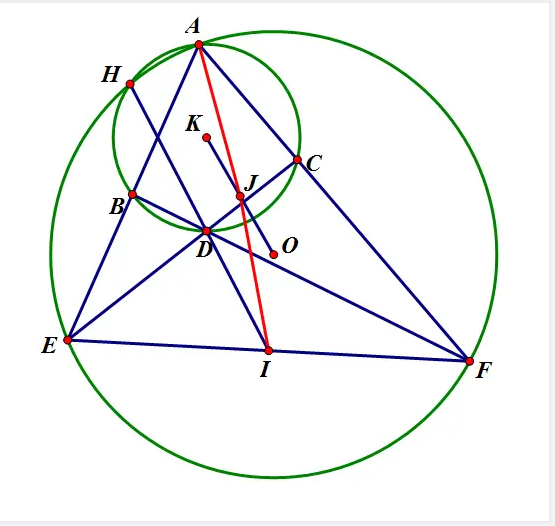
浅写蠢题,最近写的题大都不是完全自己想的,只有这个是,脑袋退化力!
先要看出费马点是中点,然后注意到相似和四点共圆,对称性乱杀。
BZ 大佬的秒杀思路,我还是太菜力!
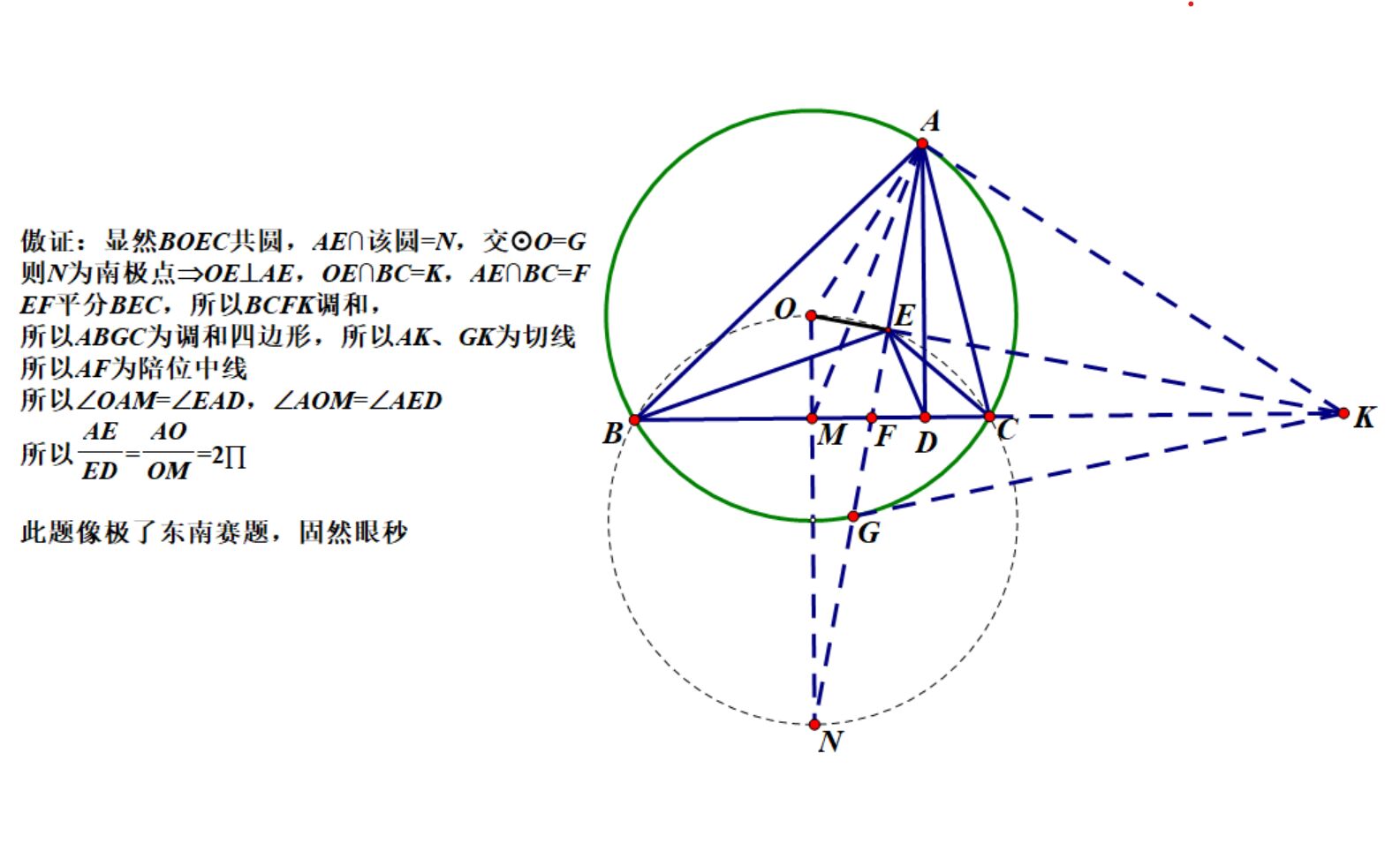
联考乱摆!
2022-10-24

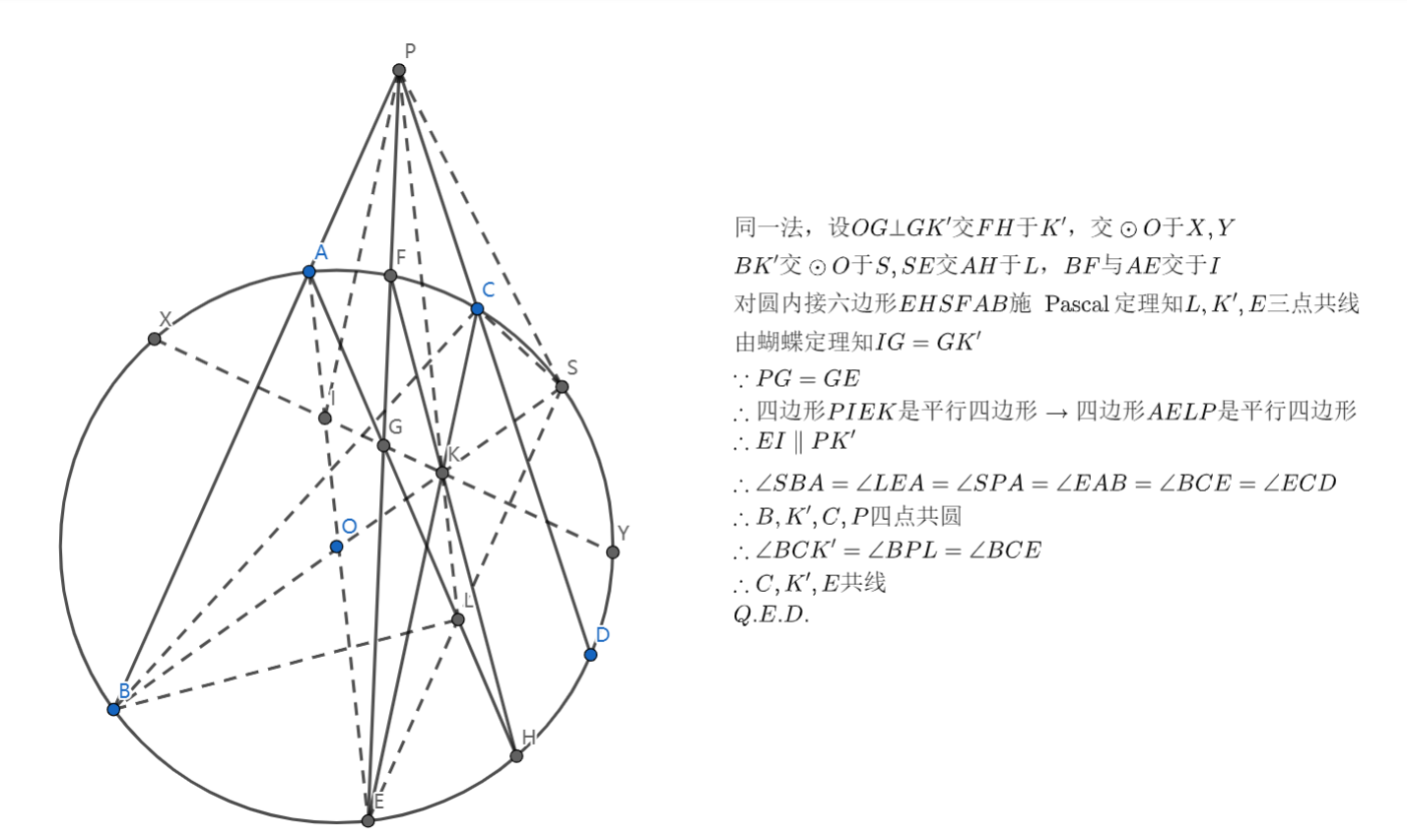
步骤中省了一个全等(证第二个平行四边形的时候)。
同一法的选取有点妙,若让 在 上就无法通过蝴蝶定理构造出一个平行四边形,证明就变的难一些。
然后是用证明两个圆周角相等的方式来同一的,比较厉害。
看了答案才会的,万喜人好难好难好难好难我还是太菜了。
我一开始想要消掉 ( 与 无关),但发现单凭 做出 是在太难,就 surrender 了,答案还是强。
顺带一提,文化课学久了我 Pascal 都看不出。
2022-10-28
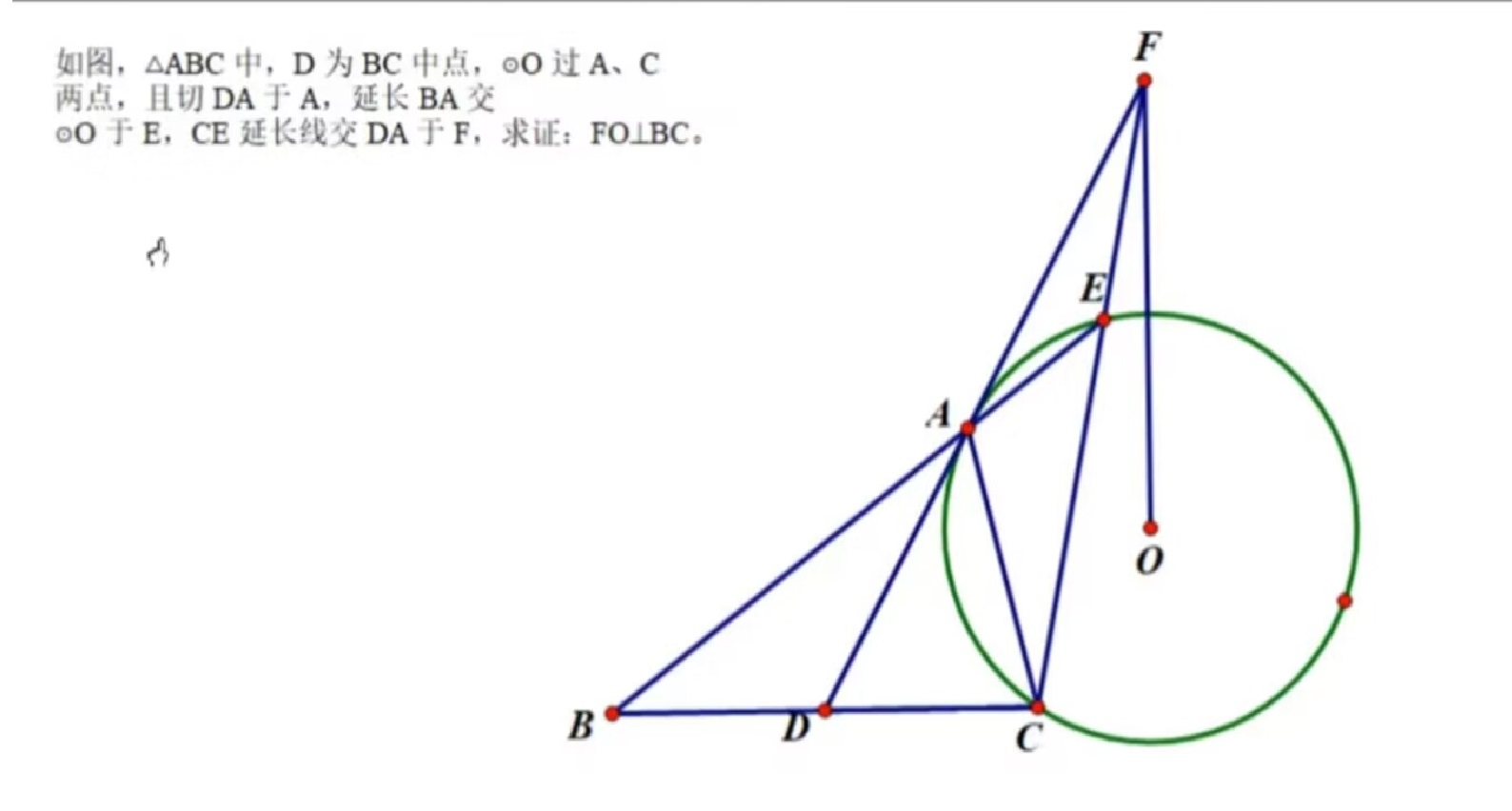
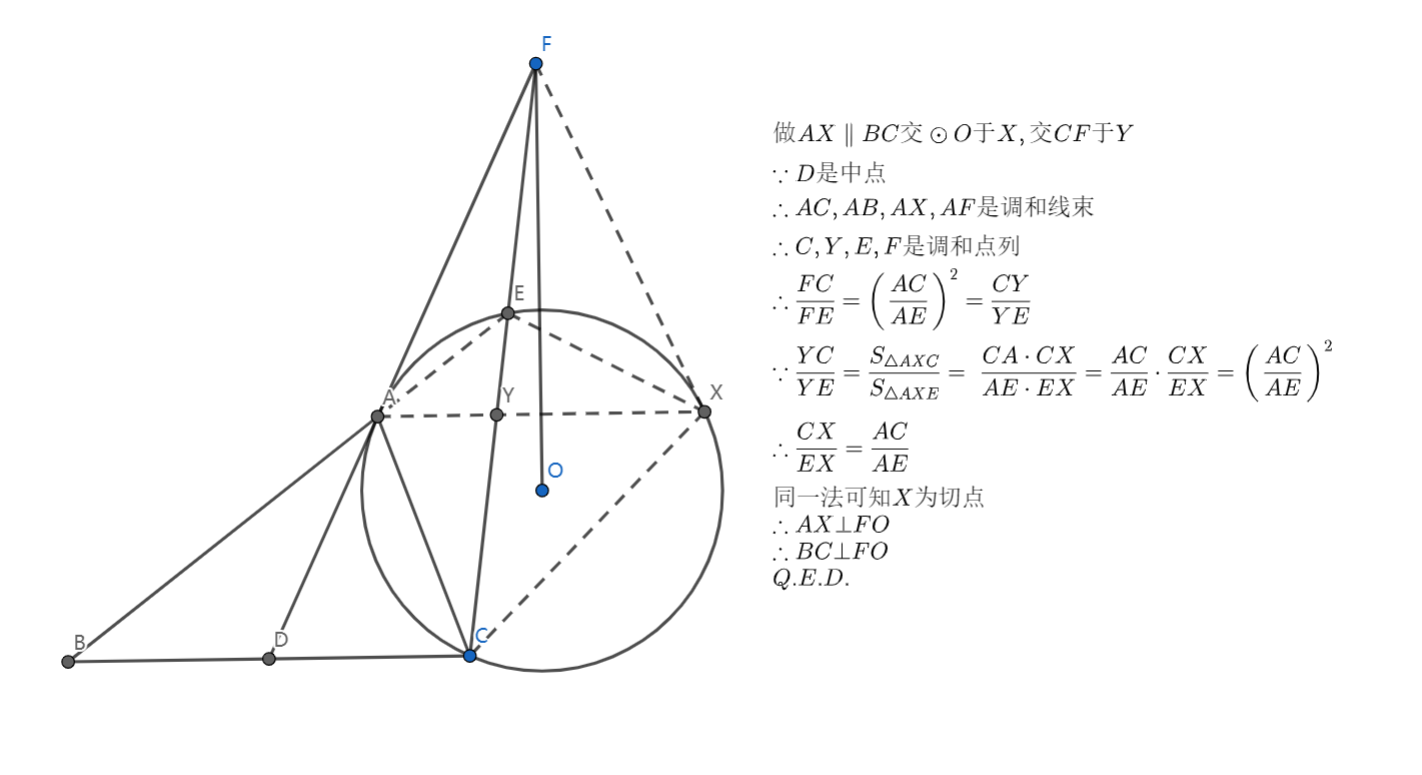
那个证切线的就是小蓝本变式,熟知结论(结果我还是写的不清不楚)。
沦落为写水题(高联难度都没有罢!)。
作者给的解法太怪了,膜!
2022-11-11
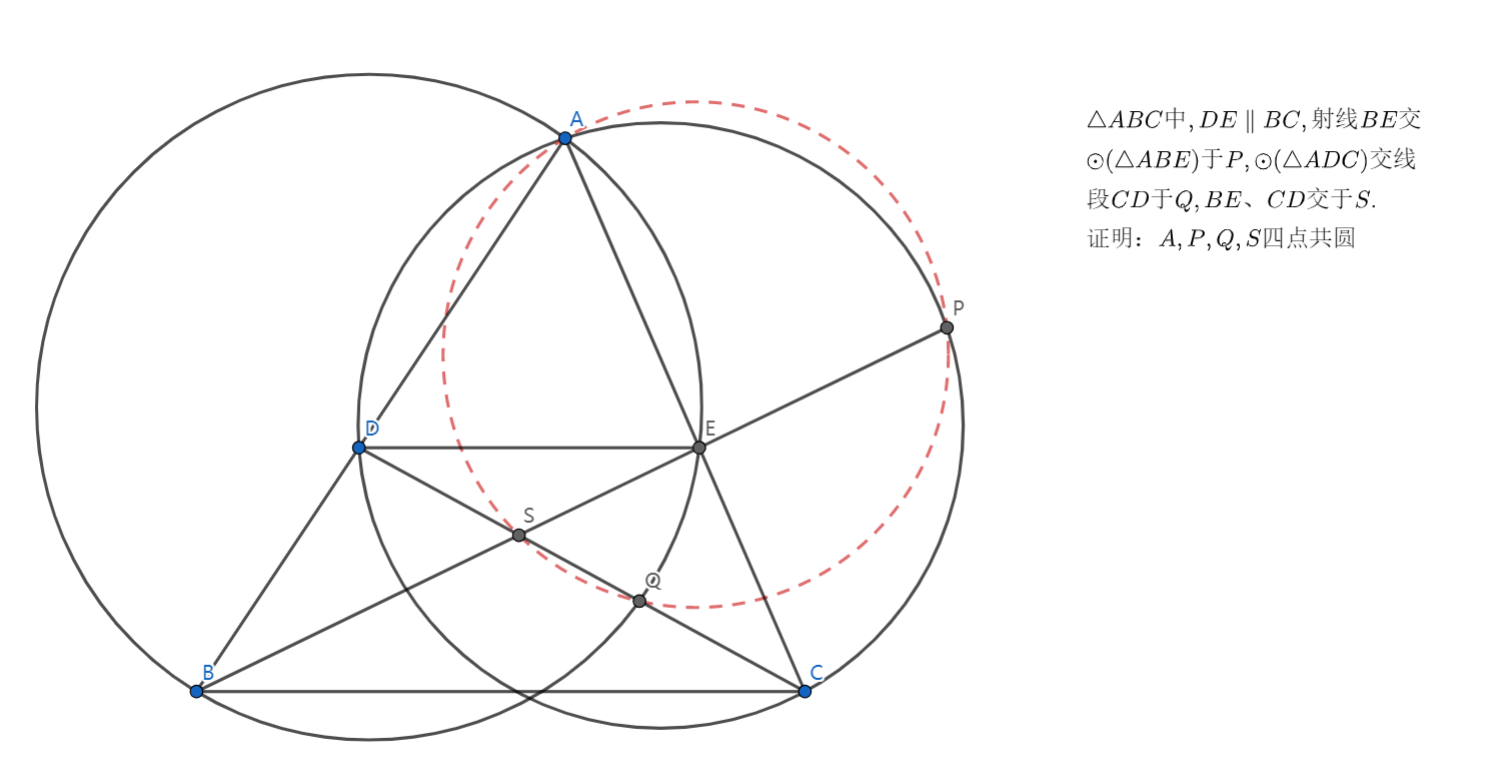
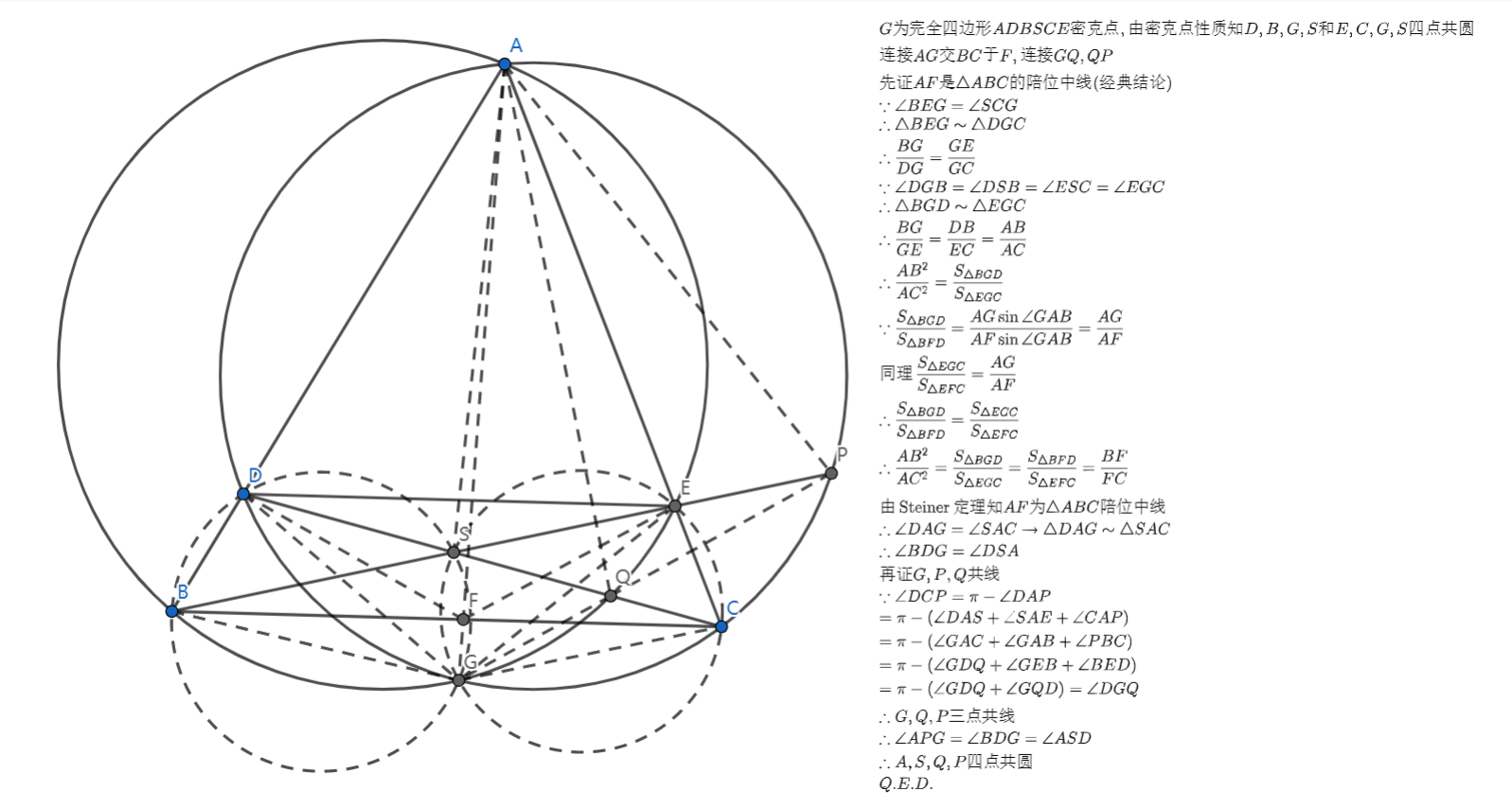
总算切了一道中等数学最后的数学奥林匹克问题上的题。
这题应该是一个经典构型出出来的,这类完全四边形 的密克点 与 的连线 是 的陪位中线是经典结论(当然是我刚学会的)。
知道这个就很轻松了。
PS:都亏我在学校看出 共线,我感觉我直觉达到了前所未有的高度。
下次整那道苏林题趴,太秀了。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现