CF1575B Building an Amusement Park
注:本文中的弧都指劣弧,角度都是弧度制(C++ 不就是吗),若无下表标记,所有角一概指内角。
Description
平⾯上有 \(n\) 个点,你要找⼀个圆,使得 \((0,0)\) 点在圆周,并且覆盖了⾄少 \(k\) 个点。
问最⼩的半径是多少。
Solution
我们不难发现,如果半径为 \(r\) 可以,那么 \(\ge r\) 的半径照样可以(答案满足单调性),所以我们考虑二分。
设我们二分了一个半径 \(r\),那么我们如何判断答案可行呢?
我们发现,\((0,0)\) 必须在圆周,那么圆心和原点的距离就是 \(r\),所以圆心可能的位置就是在以原点为圆心,以 \(r\) 为半径的圆上。
如图:
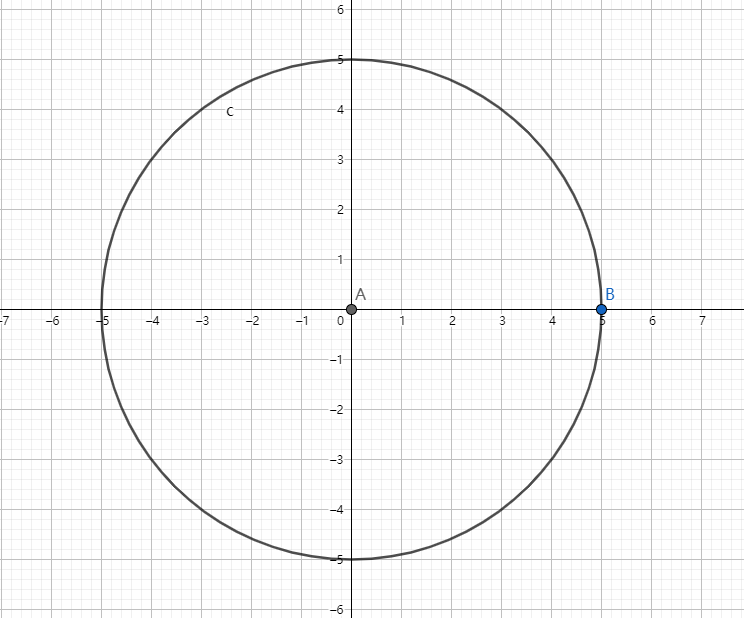
对于其他点,我们发现如果圆要包含他们,圆心一定在以这个点为圆心,以 \(r\) 为半径的圆内(注意,是圆内)。
我们假设有一个点 \(C\),假设它可以被包含,那么圆心的位置就是下图中的 \(\overset{\frown}{DE}\)(\(\odot A\)):
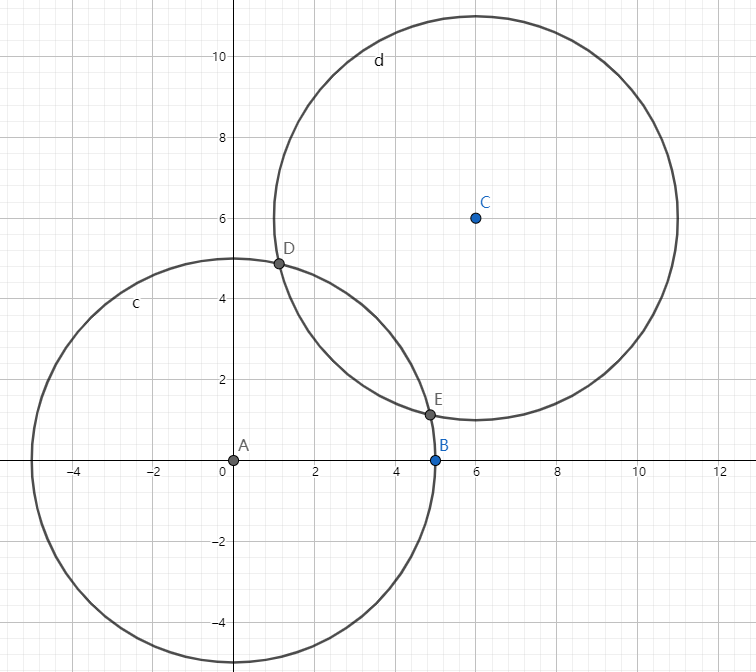
我们将这些弧都打上标记,如果有一个点被打了 \(\ge k\) 的标记,那么这个答案就一定可以。
具体怎么实现呢?
我们可以差分。
如图:
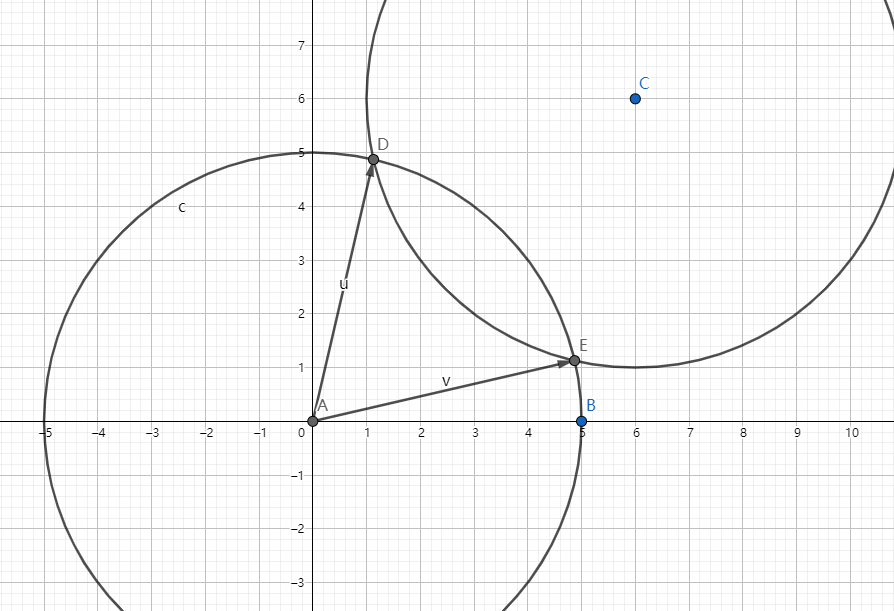
我们将 \(\vec{u}\) 和 \(\vec{v}\) 的极角打上标记(就是在 \(\vec{u}\) 打上 \(1\),在 \(\vec{v}\) 打上 \(-1\),差分都会吧?)。
最后,我们极角排序后遍历所有标记,用一个计数器 \(cnt\) 来判断标记数,如果 \(cnt \ge k\),这个答案肯定合法。
为了方便,以下负数角我们都把它转成 \([0,2\pi]\) 区间中的角(因为 \(\alpha + 2\pi\) 和 \(\alpha\) 是等价的)。
极角怎么求?
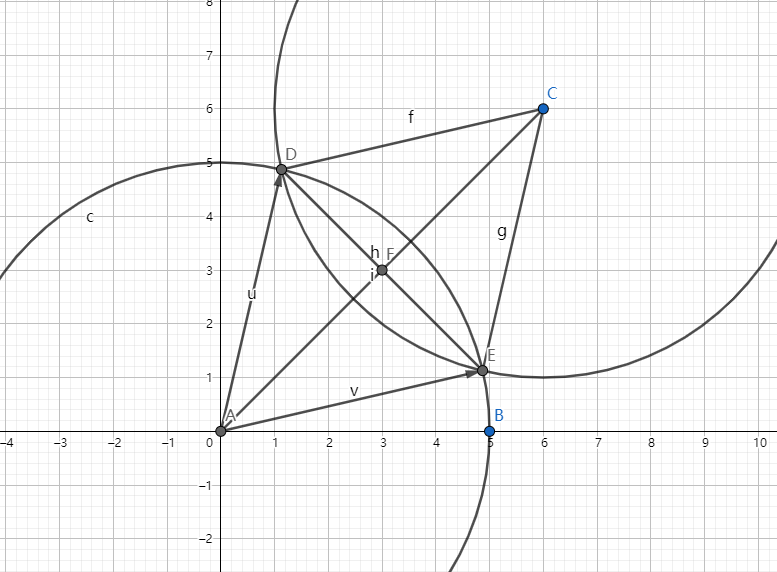
我们要求的就是 \(\angle DAB\) 和 \(\angle EAB\)。
我们设 \(\angle CAB\)(\(\overrightarrow{AC}\) 的极角)\(= \alpha\),\(\angle CAE = \beta\)
不难发现,四边形 \(ABCD\) 是菱形(四边都是 \(r\)),那么 \(AF=\frac{AC}{2}\),且 \(DE \bot AC\),那么 \(\frac{AF}{AE} = \cos \beta\),则 \(\beta = \arccos \frac{AF}{AE}\)。
所以 \(\angle DAB = \alpha + \beta\),\(\angle EAB = \alpha - \beta\)。
但这只是一种情况。
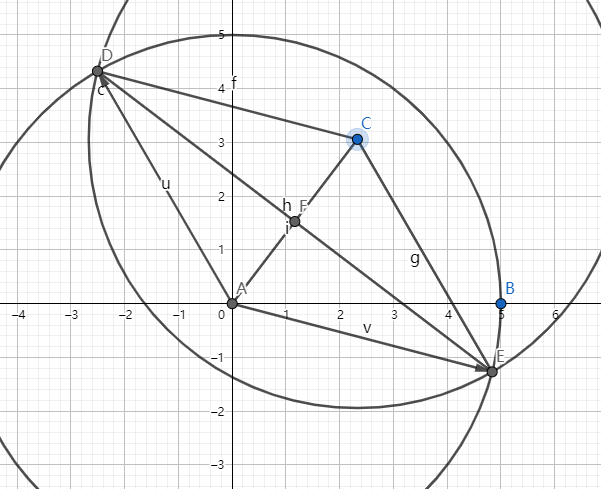
\(\alpha < \beta\) 了,我们为方便,将负数角转成正数角,即 \(\angle DAB = \alpha + \beta\),\(\angle EAB = \alpha - \beta + 2\pi\)。
但是这个时候 \(\angle EAB > \angle DAB\) 了,我们怎么打标记?
我们可以把 \(\overset{\frown}{DE}\) 拆成 \(\overset{\frown}{DB}\) 和 \(\overset{\frown}{EB}\) 两部分,分别打标记。
具体怎么写可以看代码。

我们发现这个 \(\alpha\) 是负数了,怎么办?
我们把 \(\alpha\) 加上 \(2\pi\),同第一种情况处理。
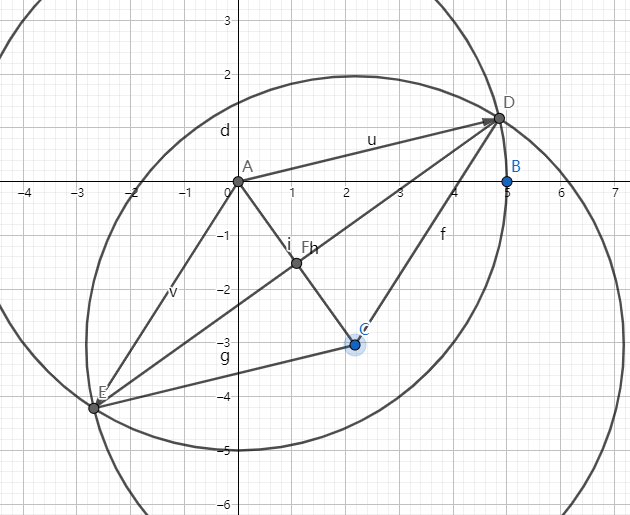
\(\alpha < 0 \and -\alpha < \beta\)。
此时 \(\angle DAB = \beta - (-\alpha) = \beta + \alpha\),\(\angle EAB_{外} = 2\pi - (-\alpha +\beta )\)。
同情况2处理。
其实情况和1情况3本质上一样,情况2和情况4也是,但我还要分讨,果然没题解贺的我就是菜狗,望 dalao 不要 D
代码(有坑,能被 hack,请自己写)
#include<bits/stdc++.h>
#define pi acos(-1)
using namespace std;
const int N=3e5+8;
const double eps=1e-6;
inline int read() {
int s=1,a=0;char c=getchar();
while(!isdigit(c)) s=(c=='-')?(-s):s,c=getchar();
while(isdigit(c)) a=(a<<3)+(a<<1)+c-'0',c=getchar();
return s*a;
}
struct vec {
double angle;
int opt;
bool operator <(const vec &fff) const {
return angle<fff.angle;
}
};
struct node {
double x,y;
} nd[N];
vector <vec> G;
int n,k;
double mx;
bool check(double mid) {
double r=mid;
G.clear();
// printf("%.5f\n",mid);
for(int i=1; i<=n; i++) {
double d=sqrt(nd[i].x*nd[i].x+nd[i].y*nd[i].y);
if(d-2*r>=eps) continue;
double alpha=atan2(nd[i].y,nd[i].x),beta=acos(d/(2*r));
if(alpha>beta&&alpha>0) {
G.push_back((vec){alpha-beta,1});
G.push_back((vec){alpha+beta,-1});
}
else if(alpha>0&&alpha<beta) {
G.push_back((vec){0,1});
G.push_back((vec){alpha+beta,-1});
G.push_back((vec){alpha-beta+2*pi,1});
G.push_back((vec){2*pi,-1});
// G.push_back((vec){alpha+2*pi});
}
else if(-alpha>beta){
alpha+=2*pi;
G.push_back((vec){alpha-beta,1});
G.push_back((vec){alpha+beta,-1});
}
else {
G.push_back((vec){0,1});
G.push_back((vec){beta+alpha,-1});
G.push_back((vec){2*pi-(beta-alpha),1});
G.push_back((vec){2*pi,-1});
}
}
int cnt=0;
sort(G.begin(),G.end());
for(auto v:G) {
cnt+=v.opt;
if(cnt>=k) return 1;
}
return 0;
}
int main() {
n=read(),k=read();
for(int i=1; i<=n; i++) {
int x=read(),y=read();
nd[i].x=x*1.0,nd[i].y=y*1.0;
mx=max(sqrt(nd[i].x*nd[i].x+nd[i].y*nd[i].y),mx);
// printf("%.5f\n",mx);
}
double l=0.0000,r=mx,ans=0.0;
while(r-l>eps) {
double mid=(l+r)/2.0;
if(check(mid)) r=mid;
else l=mid;
}
printf("%.5f",r);
return 0;
}


