DP水题乱作
George and Job
设 \(f_{i,j}\) 表示前 \(i\) 数选了 \(j\) 个区间。
不难得出转移方程 \(f_{i,j}=max(f_{i-m,j-1}+sum[i]-sum[i-m-1])\)。
其实前四道题都可以秒
Star sky
因为 \(c\) 最大为 \(10\),我们考虑将时间按 \(\mod c\) 分类,可以发现同一类的答案都是类似的。
我们对于每一个 \(t \in [0,c-1]\),求一遍二维前缀和即可。
New Year and Domino
我们考虑将可以放一个骨牌的点打上标记,做二维前缀和,但还要考虑边界情况,把骨牌出界的情况减去即可。
Coloring Trees
首先我们肯定想状态,考虑前 \(i\) 个树分成了 \(j\) 段,就有一个初步状态 \(f_{i,j}\),但是我们还要用颜色来考虑分段数,所以还要记录一个颜色 \(k\),最终状态就是 \(f_{i,j,k}\)。
我们分两种情况。
- 如果这个点没有颜色,那么我们先考虑前面一个点和它颜色相同的情况,即 \(f_{i,j,k}=min(f_{i,j,k},f_{i-1,j,k}+p_{i,k})\),在考虑不同的情况,即 \(f_{i,j,k}=min(f_{i,j,k},f_{i-1,j-1,t}+p_{i,t})\)。
- 如果这个点有颜色,那么我们还是考虑前面一个点颜色是否和它相同,如果前面一个点没有颜色,即 \(f_{i,j,k}=min(f_{i,j,k},f_{i-1,j-1,t}+p_{i,t})(t!=k),\ f_{i,j,k}=min(f_{i,j,k},f_{i-1,j,k}+p_{i,k})\)。
否则就判断前面一个点颜色是否相同,相同就 \(f_{i,j,k}=min(f_{i,j,k},f_{i-1,j,k})\),不同就 \(f_{i,j,k}=min(f_{i,j,k},f_{i-1,j-1,c_{i-1}} \ )\)。
消失之物
一个显然的背包。
少一个物品?我们先做一遍普通背包,然后把少的那个物品去掉不就好了?
「NOIP2016」换教室
最裸的暴力就是枚举换的课程,然后算答案,大概是 \(O(n^3)\) 的。
怎么办?
设 \(f_{i,j,0/1}\),表示前 \(i\) 个课换了 \(j\) 次,\(0/1\) 表示 \(i\) 是否换。
我们定义 \(v_{1}=c_{i},v_{2}=d_{i},v_3=c_{i-1},v_4=d_{i-1}\)。
大家都知道期望长度等于概率乘上路径长度,那么就有:
只是难写,思路真的简单。
[CCO2021] Bread First Search
给定一个图,添加最少的边使得它的 bfs 序为 \(1\)~\(n\)。
啥也不会?我们试着 DP。
定义 \(f_{i}\) 表示 \(1\)~\(i\) 子图的答案。
我们可以初步得出一个转移方程:
\(val(j,i)\) 表示 \((j+1)\) ~ \(i\) 中与 \(1\)~\(j\) 有边的节点数。
为什么呢?
附一张图:
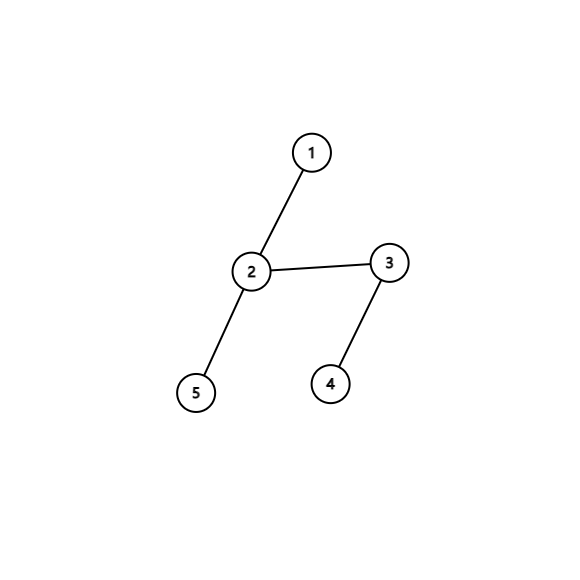
如果我们什么都不加,肯定会先访问 5 号节点。
所以我们连一条 \(3 \to 5\) 是不是可以了?
那为啥那么要有 \(\forall u \in [i,n] 与 \forall v \in [1,j] \ 没有连边\) 这个条件呢?
假设 \(i=4,j=5\)。
例如这种情况:
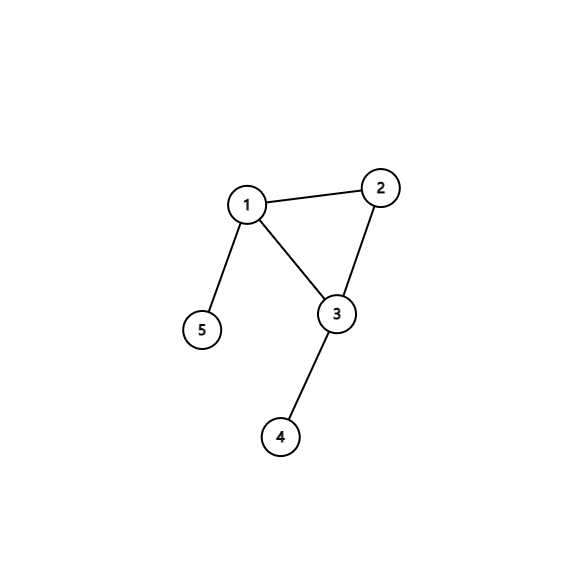
你会发现 4,5 如何连边都没有用。
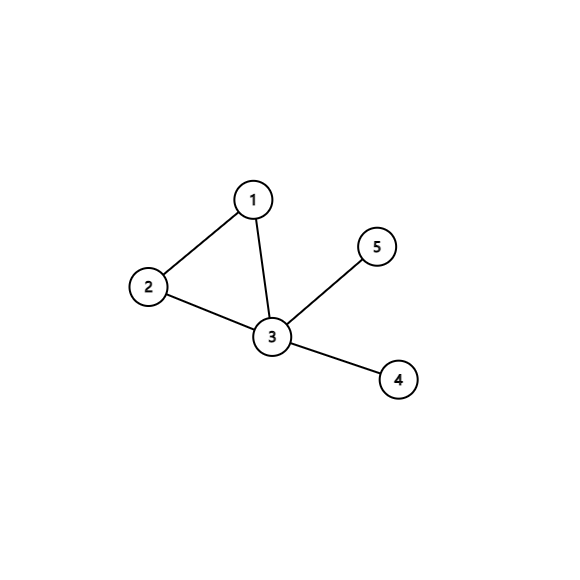
你会发现你根本不需要连边。
大概就上面两种情况。
如果直接计算,这是 \(O(n^3)\) 的。
我们设 \(s_{i,j}\) 表示 \(1\)~\(i\) 和 \(1\)~\(j\) 有边的节点个数。
你可以在 \(O(n^2)\) 的时间内预处理出 \(s\)。
具体就是把 \(i-1\) 的 \(s\) copy 过来,然后把与 \(i\) 有边的 \(j\) 的 \(s_{i,j}\) 加上成 \(1\)。
然后 \(val(i,j)=s_{i,i}-s_{i,j}+j-i\)。
那么如何优化?
考虑 \(s_{i,j}\) 的预处理,其实就是在 \(s_{i-1,j}\) 的基础上改改,我们可以用主席树优化。
至于后面的 DP,打表可知它满足决策单调性,队列优化即可。
时间复杂度 \(O(nlog^2n+nlogn)\)。
CF852B Neural Network country
给定一个除源点和汇点外有 \(L\) 层,每层 \(N\) 个点的有向图,相邻层数之间都有连边,相邻层数之间边的权值是这条边指向的点的权值(每层编号相同的点权值相同),告诉你源点到第一层边的权值,每个点的权值,最后一层到汇点的权值,求源点到汇点的路径长度能被 \(m\) 整除的个数。
先考虑 brute force : 不难发现相邻层之间点的编号影响不了什么,设 \(dp_{i,j}\) 表示在第 \(i\) 层,路径长度为 \(j\) 的方案数。
不难得出转移:\(dp_{i,j}=\sum_{k=0}^{m} dp_{i-1,j-k} \times cnt_k\),这里 \(cnt_k\) 表示 \(k\) 在相邻两层之间的出现次数。
可是在最后一层时,边的权值与点的编号有关,这个方程就不对了。
我们把最后一层和汇点的边合并,然后分开来处理。
具体来说就是这样:
My Code
for(int i=1; i<=n; i++) {
ed[(read()%m+val[i])%m]++;
}
/* dp */
for(int i=0; i<m; i++) {
for(int k=0; k<m; k++) {
f[l][(i+k)%m]+=f[l-1][i]*ed[k];
}
}
发现 \(m\) so small, \(L\) so big 不难想到矩阵乘法。
我们观察一下这个 DP:
My Code
f[0][0]=1;
for(int i=2; i<l; i++) {
for(int j=0; j<m; j++) {
for(int k=0; k<m; k++) {
f[i][(j+k)%m]+=f[i-1][j]*w[k];
}
}
}
它和矩阵乘法有着相同的性质(结合律之类的)。
这种类矩阵乘法可以这么写:
My Code
class matrix {
public:
int c[M];
matrix(){memset(c,0,sizeof(c));}
matrix operator *(const matrix &bb) const {
matrix ret;
for(int i=0; i<m; i++) {
for(int j=0; j<m; j++) {
ret.c[(i+j)%m]=(ret.c[(i+j)%m]+c[i]*bb.c[j]%Mod)%Mod;
}
}
return ret;
}
} fr,f,ed;
然后做快速幂就可以了。
[SDOI2009]学校食堂
状压牛题。
如果既从前面又从后面转移会有后效性。
但我们还是有办法。
考虑设计一个状态 \(f_{i,s,k}\) 表示考虑到了第 \(i\) 个人,从第 \(i\) 个人开始往后 \(7\) 个人的状态是 \(s\),上一个吃饭的人与 \(i\) 的距离是 \(k\)。
显然,\(k \in [-8,7]\),所以我们要加上一个 \(\Delta\) 方便储存。
考虑转移。
- 如果此时 \(i\) 已经吃饭了,那么剩下的人随便怎么吃都跟 \(i\) 无关,此时 \(i\) 的状态就可以用来转移 \(i+1\) 的状态,即
f[i+1][s>>1][delta(k-1)]=min(f[i+1][s>>1][delta(k-1)],f[i][s][delta(k)])。
这里 s>>1 和 k-1 是因为 \(i\) 与 \(i+1\) 的距离差了 \(1\)。
- 如果此时 \(i\) 还没有吃饭,那么我们就枚举 \(mxl\) 表示现在吃饭的人与 \(i\) 的距离,但此时因为 \(b_i\) 可能不一样,会出现让 \(i\) 能满意,但 \([i,i+mxl]\) 中有人不满意,这时用在记录一个 \(mxr\) 表示 \(\min \{ i+mxl+b_{i+mxl}\}\),\(mxl>mxr\) 就跳出。
转移方程即:f[i][s|(1<<mxl)][delta(mxl)]=min(f[i][s|(1<<mxl)][delta(mxl)],f[i][s][delta(k)]+(i+k>0?(t[i+k]^t[i+mxl]):0))。
答案即 \(\displaystyle\min_{k=-8}^{0} f_{n,1,k}\)。


