AGC005

这 AGC 实在是爽。

T1

括号序列（懂得都懂）

code

T2

\(O(n^2)\) 枚举每个区间是不可以的，所以我们考虑每个数的贡献。

我们可以用单调栈，找出每个 \(a_i\) 能影响到的区间 \([l,r]\)（就是以 \(a_i\) 为最小值的区间），然后方案数就是 \(f(i)=(i-l)(r-i)\)。

\(ans=\sum_{i=1}^{n} f(i)\)

code

T3

我们知道，树上最长的距离一定是直径（这不废话），每个点在树中离它距离最远的点与它的距离一定会经过直径，到达直径两端的点（这个很重要）。

最短的 \(a_i\) 一定是直径的中间那几个点。

那么 \(min(a_i) = (max( a_i )+1)/2\)

if(minn<(maxn+1)/2) {
	puts("Impossible");
	return 0;
}

然后我们分情况讨论。

如果最大值为奇数，

那么中间点有两个。

if(maxn&1) {
	if(cnt[minn]!=2) {
		puts("Impossible");
		return 0;
	}
}

然后剩下的点，我们将他关于直径的对称轴对称的点和他的 \(a_i\) 一定一样。

for(int i=(maxn+1)/2+1; i<=maxn; i++) {
	if(cnt[i]<2) {
		puts("Impossible");
		return 0;
	}
}

总共就是：

if(maxn&1) {
	if(cnt[minn]!=2) {
		puts("Impossible");
		return 0;
	}
	for(int i=(maxn+1)/2+1; i<=maxn; i++) {
		if(cnt[i]<2) {
			puts("Impossible");
			return 0;
		}
	}
	puts("Possible");
}

偶数的话，中间点就只有一个。

其他一样。

code

T4

我们考虑容斥。

设 \(F(m)\) 为满足 \(m\) 个 \(|P_i-i| = k\) 的限制。

那么 \(ans=\sum_{i=1}^{n} (-1)^{i} F(i)\)。

我们考虑将这个问题转化为二分图的形式。

（扒一张图）

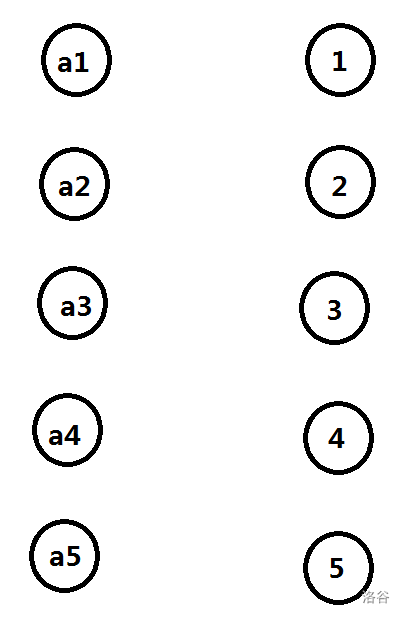
左边是权值，右边是位置。

那么我们可以根据限制条件连边。

以下是 \(n=5,k=1\) 的情况。

我们把每一条链拉平（又扒那位神犇的图）

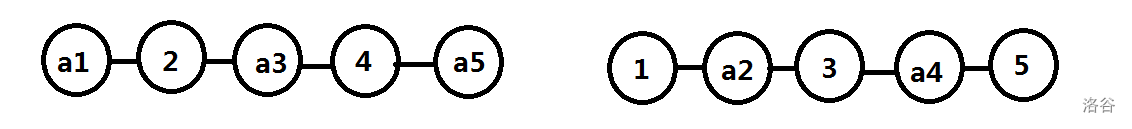
那么是不是只有相邻的边才能连边。

当然链的开头要特殊处理。

我们考虑 DP。

设 \(f_{i,j,0/1}\) 表示前 \(i\) 个点，连了 \(j\) 条边，\(0/1\) 表示 \(i,i-1\) 是否连边。

那么转移如下：

\[\begin{cases} f_{i,j,0} = f_{i-1,j,0}+f_{i-1,j,1} \\ \\ f_{i,j,1} = f_{i-1,j-1,0} (i不为链头) \end{cases} \]

那么 \(F(m) = (f_{2n,m,0}+f_{2n,m,1})\times (n-m)!\) ，大概就是钦定 \(m\) 个位置，剩下的乱选。

code

T5

这题实在 NB。

我们考虑先找到红树上能到达的点，即 \(u\) 满足 \(depa_{u} < depb_{u}\) 。

然后我们考虑有没有那种可以让先手反复横跳的点。

如果一个点到另外一个点的距离 \(\ge 3\) ，那么我们是不是一定可以让先手先到达 \(u,v\) 中的任意一点，然后反复横跳就可以让后手抓不住它。

如果没有这样的点，那么队友策略一定是在能够到达的点 \(v\) 中的 \(max(depb_{v})\) 的两倍。

因为此时的最优策略一定是到达那个点，然后在那里等待。

code

T6

显然直接考虑十分困难，我们考虑每个点的贡献。

那么不难得出包含 \(u\) 的连通块大小为 \(i\) 的方案数：

\[C(n,i) - \sum_{v\in son(u)} (i,siz_{v}) \]

那么

\[f_i = \sum_{u=1}^{n}{C(n,i) - \sum_{v \in son(u)} C(i,siz(v))} \\ \\ =nC(n,i) - \sum_{u=1}^{n} \sum_{v \in son(u)} C(i,siz(v)) \\ \]

我们设 \(cnt_i\) 表示大小为 \(i\) 的子树的数量

\[f_i = nC(n,i) - \sum_{j=i}^{n} cnt_j C(j,i) \\ \\ f_i = nC(n,i) - \sum_{j=i}^{n} cnt_j \frac{j!}{i!(j-i)!} \\ \\ f_i = nC(n,i) - \frac{1}{i!} \sum_{j=i}^{n} cnt_j \frac{j!}{(j-i)!} \\ \\ f_i = nC(n,i) - \frac{1}{i!} \sum_{j=i}^{n} cnt_j j! \frac{1}{(j-i)!} \\ \]

设 \(F_i = cnt_i i!\)，\(G_i = \frac{1}{j!}\)。

\[f_i = nC(n,i) - \frac{1}{i!} \sum_{j=i}^{n} F(j) G(j-i) \\ \\ f_i = nC(n,i) - \frac{1}{i!} \sum_{j=1}^{n-i} F(i+j) G(j) \\ \]

设 \(F^{r}(i)\) 为 \(F\) 翻转后的函数。

\[f_i = nC(n,i) - \frac{1}{i!} \sum_{j=1}^{n-i} F^{r}(n-i-j) G(j) \\ \]

这样就像一个卷积的形式了。

对了，\(924844033\) の原根是 \(5\)。

code