K-D Tree

\(K-D \ \ Tree\)

直译为K维树

如果认为我讲的不清楚可以去看 cmd 的博客

link

0x0 你要知道的

二叉搜索树的建树方式，替罪羊树的重构思想，快速排序的思想，还有简单的搜索剪枝，主定理（分析复杂度时要用），线段树之类的数据结构。

不知道也没关系

0x1算法流程

建树

首先我们来看看低维的 K-D Tree

一维的K-D Tree

因为点都在数轴上，它其实就是二叉搜索树。

我们找到区间的某个点，以该节点为此子树的根节点，然后向左右子树递归即可。

如下图，它就是一棵二叉搜索树

二维的K-D Tree

二维的 K-D Tree 我们也如一维那样构建，可是点不在数轴上了，那么我们怎么比较两个点呢？

我们任意选一条横线或数线，将平面分为两个部分，一边的是左子树，另一边的是右子树，递归即可。

举个栗子

如下图

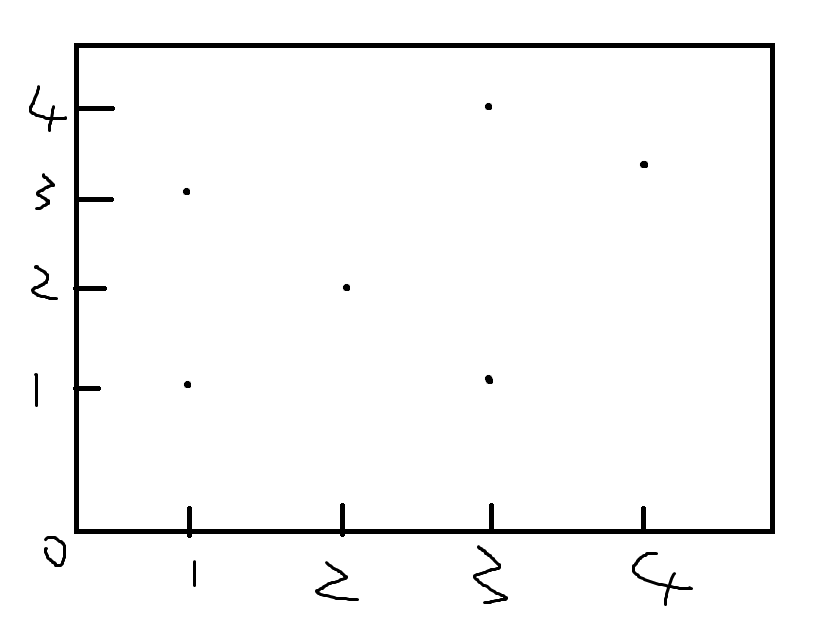
我们选择一个点，做一条经过这个点的竖线将平面分割成两部分

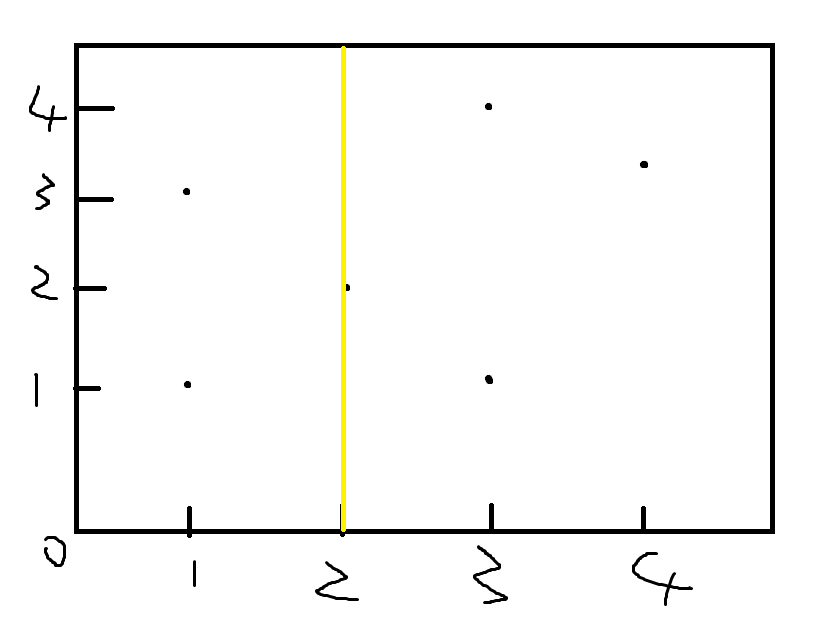
再在左右儿子各选一个点，画出两条横线

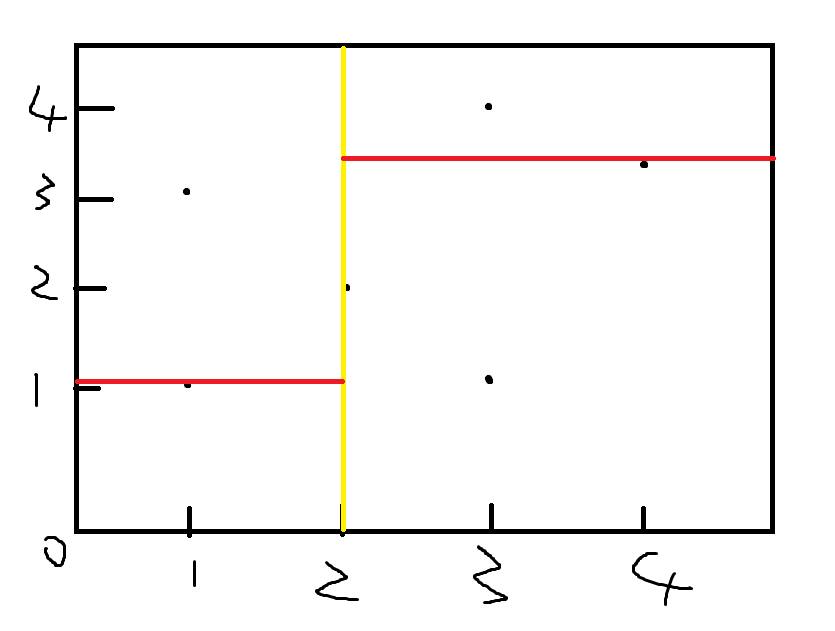
再在儿子的儿子中做一遍

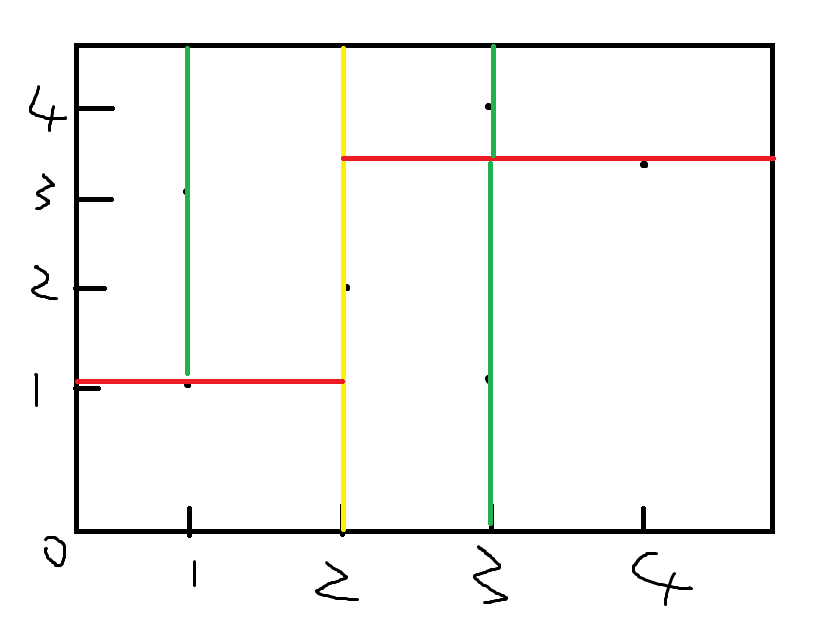
建出来的树大概长这样：

为了让这棵树是平衡的，我们每次都选点的中位数进行分割。如果每次 sort 一遍是 \(O(nlogn)\) ，最后建树的总复杂度是 \(O(nlog^2n)\) 的，显然就是逊啦不是很优秀。

考虑快速排序的本质，就是将一个数比它小的放左边，比它大的放右边，然后递归下去，这个是 $O(nlogn) $的操作，但是由于 K-D Tree 只要求要中位数在排序后正确的位置上，所以我们只需要递归排序包含中位数的 一侧，可以证明，这个复杂度是 \(O(n)\) 的。实现可以用 STL 的 nth_element

代码

struct kdTree {
	int ls,rs;
	int mn[2],mx[2];
	int val;
} tr[N];
int dim,g[N],add[N],mult[N];
bool cnp(point a,point b) {
	return a.pos[dim]<b.pos[dim];
}
bool cmp(int a,int b) {
	return cnp(s[a],s[b]);
}
int build(int l,int r,int d) {
	if(l>r) return 0;
	int mid=(l+r)>>1;
	dim=d;
	nth_element(g+l,g+mid,g+r+1,cmp);
	tr[g[mid]].val=s[g[mid]].val;
	tr[g[mid]].ls=build(l,mid-1,d^1);
	tr[g[mid]].rs=build(mid+1,r,d^1);
	pushup(g[mid]);
	return g[mid];
}

这里有一个大小优化。

• 选择的维度要满足其内部点的分布的差异度最大，即每次选择的切割维度是方差最大的维度。

代码

int build(int l,int r,int d) {
    if(l>r) return 0;
    double avx = 0, avy = 0, vax = 0, vay = 0;
    for (int i = l; i <= r; i++)
        avx += s[i].pos[0], avy += s[i].pos[1];
    avx /= (double)(r - l + 1);
    avy /= (double)(r - l + 1);
    for (int i = l; i <= r; i++)
        vax += (s[i].pos[0] - avx) * (s[i].pos[0] - avx),
         vay += (s[i].pos[1] - avy) * (s[i].pos[1] - avy);
    if (vax >= vay)
        dim = 0;
    else
        dim = 1;
    int mid=(l+r)>>1;
    nth_element(s+l,s+mid,s+r+1,cmp);
    tr[mid].ls=build(l,mid-1,d^1);
    tr[mid].rs=build(mid+1,r,d^1);
    pushup(mid);
    return mid;
}

更高维K-D Tree

像二维那样，每次比较各维的权值大小，选择点的中位数，用一个K维的超平面将K维超长方体分为两部分，再递归到子树去做。

插入&删除

由于 K-D Tree 的特殊构造方式，它不能像 Splay 那样旋转来维持平衡，FHQ 的随机优先级也不能保证其复杂度，保持其平衡的手段只有类似于替罪羊树那样的重构思想。

定义一个平衡因子 \(\alpha\) (俏佳人一般都取 \(0.7\) 或 \(0.8\) )，对于每个节点 \(x\) 如果它的任意一个字数的大小占总数的占比大于 \(\alpha\) 时就认为它不平衡，就重构，具体过程就是遍历整棵子树，将子树还原成一个序列，再构建一棵 K-D Tree 代替原来的子树。

在插入一个K维点时，通过之前建树的信息判断是因该走到左子树还是右子树，走到叶子节点的时候回溯，维护子树的信息，判断子树是否平衡并重构。

删除操作使用惰性删除，即删除一个节点是打标记，而保留其带 K-D Tree 上的位置，这样当未删除的节点树占比小于 \(\alpha\) 时，也需重构。

这样，带插入操作的 K-D Tree 的树高仍是 \(O(logn)\) 的。

详细证明参考替罪羊树的复杂度证明。

link

直接抄

查询

根据题意搜索即可。

近邻查询可以被卡到 \(O(n)\)，但在随机情况下似乎是 \(O(logn)\) 的，我并没有找到我看得懂的证明。

已经证明，在2-D Tree 上查询矩阵覆盖操作，如果已覆盖的矩阵不被查询，最优是 \(O(\log {n})\) 的，最坏是 \(O(\sqrt{n})\) 的，将结论拓展到 K 维的情况，最坏是 \(O(n^{1-\frac{1}{k}})\) 的。

关于 2-D 矩阵查询的复杂度的证明：

我们将查询矩阵分为三类：

• 与节点矩阵无交集（即 \(S_{node} \cap S_{query} = \oslash\)）
• 与节点矩阵是被包含与包含的关系 （即 \(S_{query} \sub S_{node}\)）
• 有交集 （即 \(S_{node} \cap S_{query} \neq \oslash\)）

前两种显然就直接返回了，并且前两种的子树也不会出现第三种。

所以影响复杂度的就是第三种矩阵。

我们考虑将询问看成划分 \(x,y\) ，在相邻的两轮中，分别对 \(x,y\) 划分了一次。

对于矩形的每条边，分别计算其“穿过”的节点个数，这就是需要访问的节点数。

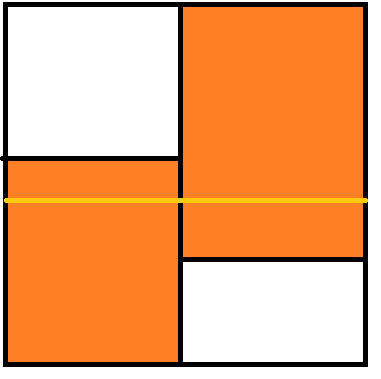
可以发现，每次我们将整个点集均分成了大小为 \(\frac{n}{4}\) 的四份，每条直线最多经过两份。

时间复杂度：\(T(n)=2T(\frac{n}{4})+O(1)\)。

根据主定理，\(T(n)=O(n^{log_{4}2})=O(n^{\frac12})=O(\sqrt{n})\)

将结论拓展至 \(K\) 维（\(K>2\)）。

我们进行 \(K\) 次划分，那么点集被划分成 \(2^{k}\) 份，一条线最多可以被截到 \(2^{k-1}\) 份。

时间复杂度就是 \(T(n)=2^{k-1}T(\frac{n}{2^{k}})+O(1)=O(n^{log_{2^{k}}2^{k-1}})=O(n^{1-\frac{1}{k}})\)。

邻值查找代码

void querymin(int u,int x) {
	if(!u) return;
	if(u!=x) ansmin=min(ansmin,dist(tr[u].x,a[x]));
	double disl=fmin(tr[u].ls,a[x]),disr=fmin(tr[u].rs,a[x]);
	if(disl<ansmin&&disr<ansmin) {
		if(disl<disr) {
			querymin(tr[u].ls,x);
			if(ansmin>disr) querymin(tr[u].rs,x);
		}
		else {
			querymin(tr[u].rs,x);
			if(ansmin>disl) querymin(tr[u].ls,x);
		}
	} else {
		if(disl<disr) {
			querymin(tr[u].ls,x);
			if(ansmin>disr) querymin(tr[u].rs,x);
		}
		else {
			querymin(tr[u].rs,x);
			if(ansmin>disl) querymin(tr[u].ls,x);
		}
	}
}

总结

K-D Tree 在很多方面都不如 CDQ ，实现难度，时间复杂度等，但是在某些毒瘤题要求强制在线还卡空间时，你就不能快乐的使用 CDQ，也不能写树套树，（毕竟线性空间的数据结构谁不爱？），而且，只要是能转化为二维或高维的问题，KDT 都能搞，十分灵活。

0x2作用(含例题和习题)

例题都是自己觉得有代表性的，自己写的。

习题一般和例题做法类似，或者比较套路，欢迎大家来切，一般不放代码(因为我不一定写)。

其实例题都是我要贺 TJ 的，习题都是我看了就能口胡出来的

最大最小距离查询

例题[SDOI2012]最近最远点对

搜索时判断到矩阵边界的距离是否大于或小于答案，如果都大于要先遍历那个大的，在决定要不要遍历另一个。否则就如果有比答案小的就哪个比答案大就遍历哪个。

代码

第K大查询

例题[CQOI2016]K 远点对

用类似于 \(A^*\) 的方法，定义一个估价函数为矩阵的边界到该点的最大距离，据此使用 \(A^*\) 即可（深度优先）。

代码

习题

• [国家集训队]JZPFAR

二维（或多维）数点问题

例题简单题

修改操作可视为插入一个点，插入时，根据这个点的坐标和树上节点的信息进行搜索，找到合适的地方就插进去，每次回溯都要更新（新插入的节点也要更新信息），不平衡时记得重构。

代码

例题[Ipsc2015]Generating Synergy

考虑转换

我们发现，子树对于 \(dfn\) 的一段区间，距离不超过 \(l\) 对应 \(dep\) ,的一段区间，那么我们珂以以把树上每一个节点抽象成一个坐标为 \((dfn_{i},dep_{i})\) 的一个点，矩阵修改，单点查询即可。

代码

例题[AHOI2008]矩形藏宝地

数点问题用烂的 trick。

我们把每个矩阵看作是一个坐标为 \((x1,x2,y2)\) 权值为 \(y1\) 的点，不难发现题目的条件就是对于每个 \((x1,x2,y2)\) 找到坐标为 \((px1,px2,py2)\) ，权值为 \(py1\) 满足 \(x1 \le px1 \ \ px2 \le x2 \ \ py2 \le y2 \ \ y1 \le py1\) 的点的个数。

三维的KDT时间复杂度明显不太够，我们把 \(x1\) 排个序，动态加点，就转化为了一个二维数点问题

代码就咕了

例题崂山白花蛇草水

矩阵查询想到 K-D Tree，第K大因为不能用堆（数据限制），所以想到权值线段树 or 主席树。

外层动态开点权值线段树查询第 K 大，内层 K-D Tree ，查询在矩阵中大于x的点的个数。

时间复杂度 \(O(q\sqrt{q}\log w)\)。

代码

以上都是口胡

好了正戏开始。

显然这个复杂度需要卡常，那怎么办呢？

例题[Ynoi2008] rrusq

大毒瘤

用了个叫根号平衡的东西。

\([l,r]\) 区间内的矩阵是不太好维护的，考虑用一种类似于扫描线的方式离线做。

我们枚举每个 \(r_i\) ，它和 \(l_i\) 的答案显然是一个后缀和，每次用 kdt 给矩阵打标记，然后统计后缀和。

但是，我们肯定会遇到一个点同时被两个不连续的矩阵包含，这个时候就要涉及到撤销。

我们维护两个 tag（kdt 上的），一个是打上标记的 tag，另外一个是清除的 tag（详情见代码）。

这样每次修改之前把子树清空（打 lazy tag），这样每次时间复杂度仍然是 \(O(\sqrt{n})\)。

考虑对每个 \(r_i\) 标记的维护。

因为可能涉及到清空矩阵时要对前面的 \(r\) 的标记进行修改，所以我们要用一种支持单点修改 \(O(m\sqrt{n})\) 次和 \(O(q)\) 次查询的数据结构，直接用 \(O(1)-O(\sqrt{m})\) 的分块即可。

这样，总的时间复杂度就是 \(O(q\sqrt{m} + m\sqrt{n})\) 。

代码

习题

• [Violet]天使玩偶/SJY摆棋子
• [SDOI2010]捉迷藏
• [BJWC2014]数据
• 巧克力王国
• 方方方的数据结构

偏序问题

例题[CH弱省胡策R2]TATT

很显然这是一个四维的偏序问题，我们按第一维排个序，就变成了最长上升子序列问题。

还是把DP式子摆一下

\(f[i]=max(f[j])+1(b[j]<=b[i],c[j]<=c[i],d[j]<=d[i]) \\ ans=max(f[i])\)

这是 \(O(n^2)\) 的，废话。

很显然是个三维偏序问题，辣么我们就可以用 cdq。

咳咳我们这里介绍的是 K-D Tree ，那我们就用 K-D Tree 写。

每次先查询已插入的点的答案，将其加一后插入到K-D Tree当中，再更新 ans 。

查询时要先判断是否在查询范围内，答案是否更优等。

代码

例题寻找宝藏

大体和上题差不多，多了个求方案数，如果你不会那只能回炉重造

再把式子摆一下

\(f[i]=max(f[j])+v[i] \\ ans1=max(f[i]) \\ g[i]= \begin{cases} \sum_{j=1}^{i} g[j] \ (f[j]=max_{k < i}(f[k])) \\ 1 \ else \end {cases} \\ ans2=g[n]\)

然后呢，然后呢就记录每个节点所管辖的范围内最大值出现的次数，查询时，判断该节点的最大值是否大于答案，如果大于就更新答案，方案数改为该节点最大值出现的次数，否则就判断该节点最大值是否等于答案，如果等于就将方案数加上该节点最大值次数。记得在开头有适当的剪枝（同上题一样）。

代码

习题

• [DBOI2019]德丽莎世界第一可爱

KDT 分治

我们简单说一下线段树分治。

当每个修改影响的询问是一个区间时，我们就可以将询问建成线段树，然后把每个修改 cover 到 \(logn\) 个询问区间上，最后在线段树上一次 dfs 就可以求出答案。

如果要做就去把 Dash Speed 多敲几遍。

KDT 分治和线段树分治基本相似，但因为 KDT 不是一个 Leafy 的数据结构，所以我们对于每个节点要记两个信息——子树矩阵的和该节点的，因为你有可能只能 cover 到这个点而不能 cover 到它的子矩阵。

例题[HNOI2016]最小公倍数

简化一下题意，给你一个 \(n\) 个点 \(m\) 条边的无向图，每条边边权是一个二元组 \(a,b\) 。

现在给出 \(q\) 组询问，每个询问是 \(u,v,x,y\) 询问 \(u,v\) 是否存在一条简单路径使得路径上的最大的 \(a\) 值和最大的 \(b\) 值是否分别为 \(x,y\)。

其实有高级的分块做法，但我只会KDT。

我们考虑一维怎么做，也就是边是 \(u,v,a\) 怎么做。

对于一条边的边权 \(a\)，它能影响到的询问一定是值域上的一段前缀，同样，我们每一个询问是对的的条件必定是一段后缀，我们把这个后缀拆成 \(log\) 个区间，然后将每条边 cover 到线段树上，然后一边 dfs 求答案即可。

二维的话，一个询问成立的条件就是 \((a,b)\) 的右上部分，KDT 分治即可。

注意，在求答案的过程中，对于每一个非叶子节点，我们做完之后一定要撤销操作，具体实现看代码，就是一个带撤销并查集。

nboj 上有点卡常。

代码

例题[PA2011]Kangaroos

题意不是一句两句能说清楚的。至少 syk 花了半天才懂

给你一个由区间组成的序列 \(A\)，每次询问一个 \([a,b]\) ，求 \(A\) 中最长的一段使得这一段的每一个区间都与 \([a,b]\) 有交。

怎么做？

暴力怎么做，暴力是不是枚举序列 \(A\)，开一个 \(cnt\) 记录长度，如果区间 \([a,b]\) 与这个元素有交，\(cnt++\)，不然 \(cnt\) 就清零。

时间复杂度 \(O(nm)\)。

考虑将区间看成点，那么没有交集的区间就是两个矩阵（具体还要你自己手动模拟去找）。

考虑对询问分治，我们将询问建成 KDT，然后将每一个区间在 KDT 上 cover。

现在你要维护的操作就是下面两个：

• 将子树的权值清空
• 将子树的权值加一

最后记录每个点的历史最大值就是每个节点的答案。

具体实现本人贺参考了一篇 TJ（@tzc_wk 的）：

我们考察一个点上一次标记下推到现在一共经历了哪些过程，有两种可能，要么没有被清空，权值直接被加上了一个数 \(v\)。要么曾经被清空过，一开始先 \(+v_0\)，然后清空，又加了 \(v_1\)，再清空，\(+v_2\)，清空，……，最后 \(+v_m\)，值为 \(v_m\)。不难发现由于我们只关心历史最大值，因此 \(v_1,v_2,\cdots,v_m\) 具体是什么不重要，我们只用关心以下几个值：

• 第一次加的值 \(v_0\)，程序中用 \(add\_mx\) 表示。
• 这个值从上一次被标记下推是否被清空，\(clr\)。
• \(max \ v_1,v_2,\cdots,v_m\)，程序中用 \(cov\_mx\)表示。
• 这个位置当前的值 \(v_m\)，程序中用 \(tg\) 表示。

当然除了这四个标记之外，还有每个位置的权值 \(v\) 以及历史最大值 \(hmx\)。

考虑对一个子树清空/整体加值会对标记产生怎样的影响。首先是子树清空，这个比较容易，直接将 \(clr\) 设为 \(1\)，\(tg,v\) 设为 \(0\) 即可。其次是整体加值，如果 \(clr\ne 0\) 那就令 \(tg\) 加 \(v\)，并将 \(cov\_mx\) 对 \(tg\) 取 \(\max\)，否则令 \(add\_mx\) 加 \(v\)。

然后是下推标记的问题，如果 \(clr=0\) 那么直接对左右儿子进行整体 \(+add\_mx\)，然后 \(+v_1\)，清空，\(+v_2\)，清空，……，最后 \(+v_m\)，这等价于先对左右儿子进行整体 \(+add\_mx\) 对该节点的 \(cov\_mx\) 取 \(\max\)，然后令左右儿子的 \(tg\) 和 \(v\) 都等于 \(tg\)。注意每次操作之后都要实时更新 \(hmx\)。

在 \(pushdown\) 中更新 \(hmx\) 的方式就是将 \(hmx\) 与 \(cov\_mx\) 去个 \(\max\)，因为 \(cov\_mx\) 中记录的就是在这段区间中（上次清空和这次清空的这段区间）的历史最大值。

代码

优化建图

例题[NOI2019] 弹跳

暴力（1~8）

每次遇到一个点就遍历一遍属于它的弹跳装置，然后暴力连边，空间复杂度 \(O(nm)\) 。还有32分呢，这不比省队集训好

特殊性质一（9~13）

直接连边即可。

特殊性质二（14~18）

线段树优化建图啊。因为我们这里不是讲线段树，所以不展开来讲。空间复杂度 \(O(n+mlogn)\) ，时间复杂度 \(O((n+mlogn)log(n+mlogn))\) 。

(19~22) & (23~25)

23~25是用来卡 SPFA 的。

对于每一个城市 \(C \in [1,n]\) ，我们都把它先向K-D Tree上的与它对应的节点 \(C+n\) 连一条边( \(C+n \to C\))。然后我们遍历每一个弹跳机，假设它起点城市为 \(u\)。遍历过程中，对于每个树上节点 \(x\) ，如果它维护的矩阵在弹跳机的范围外自然就返回，否则我们判断它维护的矩阵是否被该弹跳机的矩阵包围，是的我们就连一条 \(u \to x\) 的边返回，否则：如果树上节点 \(x\) 对应的城市 \(C\) 满足在弹跳机的范围内，我们就连一条边 \(u \to x-n\) ，\(x-n\) 就是 \(x\) 对应的城市，然后查询左右儿子。

这样其实和暴力差不了多少，我们考虑优化一下。

我们建图的目的是什么？当然是知道这个点可以走到哪里。

知道这一点你就可以写了。

我们考虑在跑最短路的途中，对于每一个城市 \(C\) ，我们直接遍历每一个属于它的弹跳机，对于树上每一个节点 \(x\) ,我们按刚才说的方法判断，把刚才说的方法中的连边改成更新并加入队列即可。

时间复杂度 \(O(m\sqrt{n}logn)\) 。但因为 ccf 的原因跑不满，卡卡常就过了。

在uoj我的会被hack，但我亲眼看见一个和我做法一样的人过了(还挺多)，所以不要借鉴我的大常数代码

最后不忘附上一句，关于 spfa ，它死了

代码