[NEERC2017]Connections

题目大意给你一个\(n\)个点，\(m\)条边的有向图，要你删\(m-2n\)条边，不改变图的连通性
首先我们考虑tarjan
考虑哪些边必须留下
缩完点之后剩下的的边肯定不用留下
每个连通块无非就是三种边:
1.搜索树上的边
2.返祖边
3.横叉边
横插边没有什么意义
那么只有搜索树上的边和一些返祖边要留下
是那些返祖边呢？
如图:

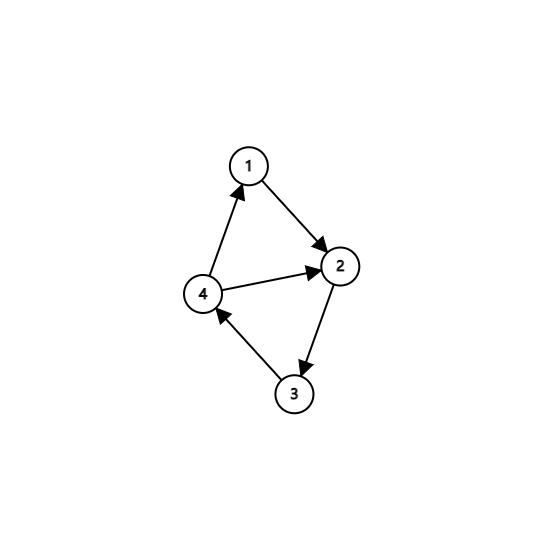
显然，肯定不能删\(4->1\),所以要把\(4->2\)删掉
所以只要保留该节点与该节点的low的边
跑一边tarjan，把该删的边删掉即可
时间复杂度\(O(n+m)\)

#include<bits/stdc++.h>
using namespace std;
inline int read() {
	int s=1,a=0;
	char c=getchar();
	while(!isdigit(c)) {
		if(c=='-') s=-s;
		c=getchar();
	}
	while(isdigit(c)) {
		a=a*10+c-'0';
		c=getchar();
	}
	return s*a;
}
const int N=1e5+8;
struct edge {
	int nxt,to,from;
} e[N<<1];
int head[N],idx;
void add(int u,int v) {
	e[++idx].nxt=head[u];
	e[idx].from=u;
	e[idx].to=v;
	head[u]=idx;
}
int n,dfn[N],low[N],sta[N],instack[N],cnt,vis[N],top,col[N],siz[N],num,m;
void tarjan(int u) {
	dfn[u]=low[u]=++cnt;
	instack[u]=1;
	sta[++top]=u;
	for(int i=head[u]; i; i=e[i].nxt) {
		int v=e[i].to;
//		if(v==fa) return;
		if(!dfn[v]) {
			vis[i]=1;
			tarjan(v);
			low[u]=min(low[v],low[u]);
		} else if(instack[v]) {
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]) {
		num++;
		int x=sta[top];
		while(x!=u) {
			x=sta[top--];
			instack[x]=1;
			col[x]=num;
			siz[num]++;
		}
		top--;
		instack[u]=1;
		col[u]=num;
		siz[num]++;
	} else {
		for(int i=head[u]; i; i=e[i].nxt) {
			int v=e[i].to;
			if(dfn[v]==low[u]) {
				vis[i]=1;
				break;
			}
		}
	}
}
int t;
int main() {
	t=read();
	while(t--) {
		memset(col,0,sizeof(col));
		memset(siz,0,sizeof(siz));
		memset(vis,0,sizeof(vis));
		memset(dfn,0,sizeof(dfn));
		memset(e,0,sizeof(e));
		memset(head,0,sizeof(head));
		cnt=num=top=idx=0;
		memset(sta,0,sizeof(sta));
		memset(instack,0,sizeof(instack));
		n=read(),m=read();
		for(int i=1; i<=m; i++) {
			int u=read(),v=read();
			add(u,v);
		}
		int f=m;
		for(int i=1; i<=n; i++) {
			if(!dfn[i]) tarjan(i);
		}
		for(int i=1; i<=m; i++) {
			if(!vis[i]) {
				f--;
				printf("%d %d\n",e[i].from,e[i].to);
				if(f<=2*n) {
					break;
				}
			}
		}
	}
	return 0;
}