第四章——训练模型（Training Models）

前几章在不知道原理的情况下，已经学会使用了多个机器学习模型机器算法。Scikit-Learn很方便，以至于隐藏了太多的实现细节。

知其然知其所以然是必要的，这有利于快速选择合适的模型、正确的训练算法、合适的超参数。了解底层有助于更有效率地调试问题以及平台错误。

本章从现行回归模型开始，讨论两种不同的训练方式：

• 直接使用解析解，例如一元二次方差的求根公式。
• 有些数学问题（比如大多数偏微分方程）是没有数值解的，这时候就要用数值解来近似求解。有时间为了效率，解释存在解析解，也是求近似的数值解。

4.1 线性回归（Linear Regression）

4.1.1 线性回归模型解析解

方程4-1.线性回归模型预测

$\hat{y} = \theta_0 + \theta_1x_1 + \theta_2x_2 + \dots + \theta_nx_n$

• $\hat{y}$是预测值
• $n$是样本总数
• $x_i$是第$i$个样本值
• $\theta_j$是第$j$个模型参数（包括偏置项$\theta_0$和特征权重$\theta_1,\dots,\theta_n$）

使用向量化的形式可改写为

$\hat{y} = h_{\theta}(X) = \theta^T \cdot X$

线性回归模型损失函数（cost function）

$MSE(X,h_{\theta}) = \frac{1}{m} (\theta^T \cdot X^{(i)} - y^{(i)})^2$

通过求偏导，求极值点，可得到

$\hat\theta = (X^T \cdot X)^{-1} \cdot X^T \cdot Y$

• $\hat\theta$是使得损失函数最小的$\theta$
• $Y$是目标值向量，包含$y^{(1)}$到$y^{(m)}$

4.1.2 计算复杂度（Computational Complexity） 

求解析解时，有一个对$X^T \cdot X$求逆的操作，这是一个$n \times n$矩阵（$n$是特征总数）。对这样一个矩阵求逆的复杂度大概是$O(n^{2.4})$到$O(n^{3})$（根据不同的实现方法有不同的结果，具体是怎么得到的，有空我再看看矩阵论吧）。

另一方面，训练样本数量对计算复杂度的影响是线性的，也就是$O(m)$，所有处理大训练集是高效的，只要内存足够。

4.2 梯度下降（Gradient Descent）

假设你迷失在山间并且浓雾袭来，你只能看到脚下山坡的斜率。快速下山的一个策略就是，没走一步都沿着最陡峭的斜坡下山。这也是梯度下降所采用的策略：计算损失函数关于当前参数向量$\theta$的梯度， 沿着梯度下降的方向改变$\theta$。当梯度为0时就取得了最小值。

梯度下降的一个重要参数是步长，由学习率这一超参数决定。学习率过小会延长训练时间，学习率太大又会导致不能收敛。而且并不只是所有的损失函数都是连续可微，并只有一个全局最优解的。不过MSE损失函数是凸函数，全局可微并只有一个极值点。

事实上，MSE的函数图像是碗形，但如果特征间取值尺度不同，它可能就是一个瘦长的碗形。在图4-7中，左侧训练数据的两个特征有相同的取值尺度。右侧特征1的取值要远小于特征2。

图4-7 Gradient Descent with and without feature scaling

左侧的梯度下降算法笔直地走向最低点，因为速度较快。而右侧绕了弯弯，这就需要较长的迭代时间。

当使用梯度下降时，首先确保特征具有相同的数据范围（比如使用Scikit-Learn’s StandardScaler进行处理）。

上图也阐明了，训练一个模型实际上就是寻找一组使得损失函数取值最小（在训练集上）的模型参数。这需要在模型的参数空间进行搜索，该空间维数越高越棘手。不过如果损失函数是凸函数，那就好多了。

4.2.1 批梯度下降（Batch Gradient Descent，BGD）

首先求个模型参数关于损失函数的偏导数：

$\frac{\partial }{\partial \theta_j} MSE(\theta) = \frac{2}{m} \sum_{i=1}^{m}(\theta^T \cdot X^{(i)} - y^{(i)})x_j^{(i)}$

本文中的$ \cdot$统一都是矩阵乘法，不是矩阵点乘。

除了单独计算每一个偏导数，我们也可以使用向量化的方式，统一计算所有的偏导数：

\begin{align*}
\nabla_\theta MSE(\theta) = \begin{pmatrix}
\frac{\partial }{\partial \theta_0} MSE(\theta) \\
\frac{\partial }{\partial \theta_1} MSE(\theta) \\
\vdots \\
\frac{\partial }{\partial \theta_n} MSE(\theta)
\end{pmatrix}
= \frac{2}{m}X^T \cdot (X \cdot \theta - Y)
\end{align*}

上面这个矩阵运算，$X$是$m \times n$矩阵，$m$是样本数，$n$是特征数。$X^T$是$n \times m$矩阵，$\theta$是$n \times 1$矩阵，$Y$是$m \times 1$矩阵。

注意到上式中每一次迭代，都要使用整个训练集来计算梯度。这就是该算法之所以被称为批梯度下降。当数据集巨大时会变得很慢。不过好的是，该算法在特征数较多时仍然表现良好。

迭代公式如下：

$\theta^{(next\ step)} = \theta - \eta \nabla_\theta MSE(\theta)$

其中$\eta$是学习率。可以使用网格搜索寻找合适的学习率。当然，为了识别出造成收敛过慢的学习率，我们还要设置迭代次数。迭代次数太小，可能还没有收敛；迭代次数过大，又会浪费时间。通常的做法是，设置一个很大的迭代次数，但是当偏导数的模小于某个极小值$\varepsilon$时，就停止迭代。

4.2.2 随机梯度下降（Stochastic Gradient Descent，SGD）

批梯度下降最大的问题就是每次迭代，都要使用整个训练集来计算梯度。而SGD是另一个极端：每次迭代，只随机选择一个样本来计算梯度。这使得一次迭代的计算量大大减小。这也可以来训练海量数据集，因为每次只选择一个样本放进内存去计算。SGD也可以用来实现在线学习算法（或者out-of-core algorithm）。

另一方面，由于SGD随机的属性，每次迭代会造成损失函数忽大忽小，不过在平均的意义上是减小的。迭代将停在最小值附近，但可能始终无法达到最小值。随意当算法结束，得到的参数是不错的，但不是最优。

当损失函数有多个极值点是，SGD比BGD更容易跳过局部最优而找到全局最优。

所以随机的优势是避免陷入局部最优，劣势是永远无法达到最小值。一个解决方案只逐步地减小学习率。刚开始时学习率比较大（这有助于加快进度以及避开局部最优），随后越来越小，最终得到全局最优。这一过程被称作模拟降温（simulated annealing）算法，因为它类似于冶金时金属的逐渐降温。决定每次迭代学习率的函数被称为学习计划表（learning schedule）。

4.2.3 最小批梯度下降（Mini-batch Gradient Descent）

Mini-batch GD每次计算梯度是，都会随机选择一批实例，这批实例被称作mini batches。Mini-batch GD优于SGD之处在于，前者可以利用矩阵运算的硬件优化，尤其是使用GPU时。并且前者更稳定，更容易接近最优质，但也更容易陷入局部最优。

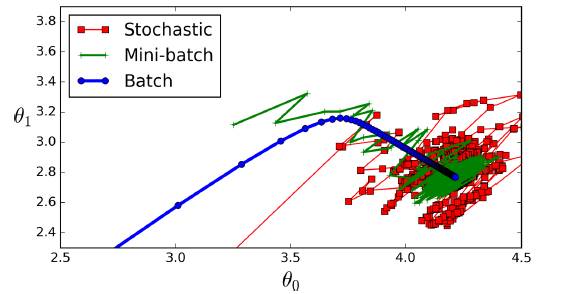
梯度下降在参数空间的路径

我们可以比较一下求解线性回归模型各种算法的优劣（m是训练样本数，n是特征数）：

Algorithm	Large m	Out-of-core support	Large n	Hyperparams	Scaling required	Scikit-Learn
Normal Equation	Fast	No	Slow	0	No	LinearRegression
Batch GD	Slow	No	Fast	2	Yes	n/a
Stochastic GD	Fast	Yes	Fast	$\geq$2	Yes	SGDRegressor
SGDRegressor	Fast	Yes	Fast	$\geq$2	Yes	n/a

4.3 多项式回归（Polynomial Regression）

其实可以用线性回归模型拟合非线性数据，简单的做法是增加每个属性的次方作为新的属性。这被称作多项式回归。

m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly_features = PolynomialFeatures(degree=2, include_bias=False)
>>> X_poly = poly_features.fit_transform(X)
>>> X[0]
array([-0.75275929])
>>> X_poly[0]
array([-0.75275929, 0.56664654])

上面的代码只有一个属性$x$，使用二次函数对其拟合，只需要增加一个$x^2$的属性即可。

如果训练样本有多个属性，还要增加不同属性的组合，作为新的属性。例如，有$a$、$b$两个属性，需要增加的新属性有：$a^2$、$a^3$、$b^2$、$b^3$、$ab$、$ab^2$、$a^2b$。

PolynomialFeatures(degree=d)将$n$个特征扩充为$\frac{(n+d)!}{d!n!}$个特征。 其实就是n元d次完全多项式的项数，至于这个排列组合问题是怎么求解的，我还没搞明白。

4.4 学习曲线（Learning Curves）

学习曲线就是绘制出随着训练集的增大，模型在训练集和测试集上的性能。

作者在最后提到了The Bias/Variance Tradeoff。之前一直行不通这里的Bias和Variance该怎么翻译。Bias不是上文提到的偏置项，Variance也不应该翻译为方差。Understanding the Bias-Variance Tradeoff这篇文章讲的挺好的。我只读了这篇文章的1.1和1.2，有空翻译一下整篇文章。

我们先介绍一下Bias和Variance

Bias衡量了模型预测的精准性，也就是平均预测值和真实值的差异。平均预测值，是指使用不同的训练数据，分别对模型进行训练，然后进行预测。Bias可以简单地理解为训练集的误差，Bias越大，训练集误差越大。

Variance衡量了模型预测的确定性，也就是对同一个样本点预测稳定性。对于一个给定的待预测样本点，使用不同的训练数据分别训练模型，然后进行预测。这组预测值的方差越小，则该模型越稳定。这跟预测的准不准没关系，只看预测的稳不稳。对于分类问题，Variance越小，决策边界受到训练数据的影响就越小。Variance太大，不同的训练集会得到差异很大的决策边界。

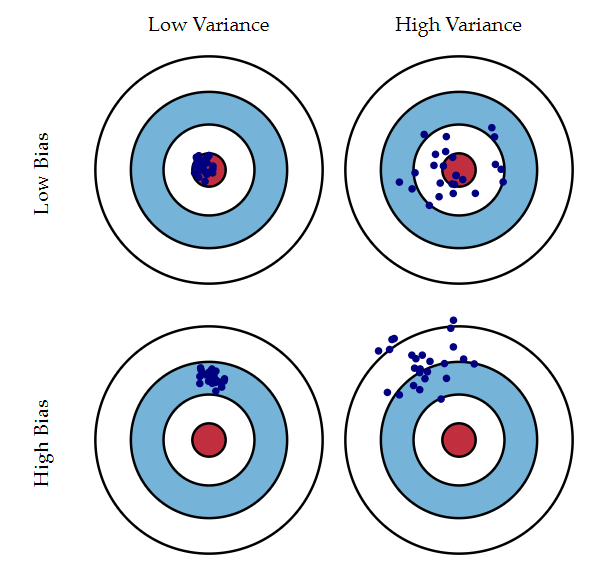
上图描述了二者之间的关系。这是用不同的训练数据对模型进行训练，每次训练之后都对测试集的一个确定的样本点进行预测，小蓝点是预测值，红圈的正中心是真实值。

通常情况下，对于一批训练数据，使用不同的模型，Bias和Variance此消彼长的。

机器学习的错误一般分为以下三类：

• high-Bias：一般是优化假设有误，比如假设数据是线性的，实际上是二次的。这种模型对训练数据欠拟合
• high-Variance：这是由于模型对训练数据的微小变化过于敏感。高自由度的模型（比如高纬度的多项式）容易造成high-Variance，这种模型对训练数据过拟合。
• Irreducible error：这是由于数据自身的噪音，智能通过数据清洗解决，比如删除离群点。

降低模型复杂度会增加Variance，减小Bias。反之亦然。

4.5 线性模型正则化（Regularized Linear Models）

4.5.1 岭回归（Ridge Regression）

$J(\theta) = MSE(\theta) + \alpha\frac{1}{2}\sum_{i=1}^{n}\theta_i^2$

对损失函数增加正则项，降低模型复杂度，降低过拟合的风险。其中$\alpha$是个超参数。

需要说明的是，

• 训练模型时增加正则项，但是用测试集评估模型时，就不能使用正则项了。模型训练和模型评估使用不同的损失函数是很常见的。除了正则化，另一个原因是训练时的损失函数需要便于求导，但是在测试集评估时就要与目标值尽可能接近。例如，逻辑回归在训练时使用log loss作为损失函数，但是评估时使用精度/召回率。
• $\theta_0$不进行正则化。
• 训练之前，统一数据不同属性的取值范围很重要（比如使用StandardScaler），绝大多数的正则化模型都需要这么做。

岭回归解析解：

$\hat\theta = (X^T \cdot X + \alpha A)^{-1} \cdot X^T \cdot Y$

其中，$A$是个近似的$n \times n$的单位矩阵，只是左上角是个0。其实正则化带来了一个额外的好处，那就是矩阵$(X^T \cdot X + \alpha A)$一定可逆（听吴恩达课的时候，他说的一定可逆，但我没有去研究数学原理，矩阵论忘得差不多了），从而解析解一定存在。但是求线性回归解析解时，$(X^T \cdot X )^{-1}$可能是不可逆，尤其是特征数远远大于样本数时。

4.5.2 Lasso Regression

损失函数：

$J(\theta) = MSE(\theta) + \alpha\sum_{i=1}^{n}\left | \theta_i \right |$

Lasso回归倾向于去除掉最不重要的特征（也就是将其权重设置为0）。

图4-19 Lasso和Ridge正则化对比

在上图左上角中，背景的椭圆轮廓代表为正则化的MSE损失函数（也就是$\alpha$为0），小白点代表该损失函数的BGD路径。前景的菱形代表$l_1$惩罚（也就是设置$\alpha \rightarrow  \infty$），小黄三角代表该惩罚的BGD路径。这一路径首先到达$\theta_1 = 0$的点，然后到达$\theta_2 = 0$的点。右上角代表Lasso回归并设置$\alpha = 0.5$。其BGD路径也倾向于一个参数值先达到0。相似的，小面两幅图使用的是$l_2$正则项。与未正则化相比，$l_2$正则的参数项更接近于$\theta = 0$点，但是并没有那个参数值被干掉。

Lasso回归在$\theta_i = 0$点是不可微的，梯度下降依然可以工作，如果使用次梯度（作者解释说，次梯度可以理解为不可微点周围梯度的中间值）。

4.5.3 Elastic Net 

Elastic Net介于Ridge回归和Lasso回归之间，损失函数如下：

$J(\theta) = MSE(\theta) + \gamma \alpha\sum_{i=1}^{n}\left | \theta_i \right | + \frac{1-\gamma}{2}\alpha \sum_{i=1}^{n}\theta_i^2$

Ridge一般是个不错的选择。如果你怀疑只有一部分样本时有用的，那可以选择Lasso或者Elastic Net，因为它们倾向于将不重要特征的权重设置为0。Elastic Net比Lasso表现会好一些，由于后者在特征数多于实例数或者一些特征间存在强关联时，会表现得不稳定。

4.5.2 提前停止训练（Early Stopping）

对于迭代学习算法，除了上面提到的，还有一种完全不同的正则化方式，那就是当校验集的误差达到最小时，就提前停止训练，这被称作Early Stopping。

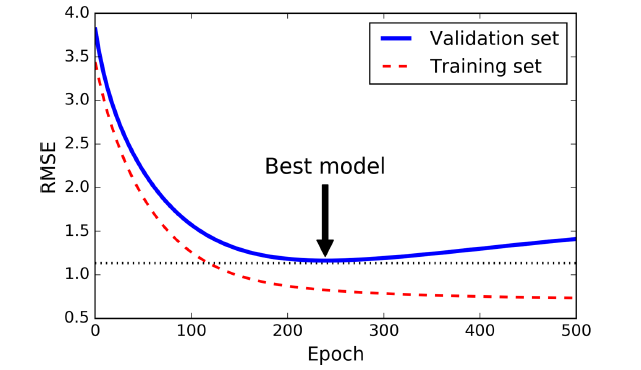
图4-20. Early stopping正则化

上面显示了使用BGD训练一个复杂模型（比如高阶多项式回归）。在训练前期，伴随着迭代周期的增长，训练集和校验集的RMSE都在减小。但是随后校验集的误差开始增大，这表明模型开始过拟合训练数据。我们在校验集误差最小的训练周期停止训练。

4.6 逻辑回归（Logistic Regression）

4.6.1 评估概率（Estimating Probabilities）

和线性回归类似，逻辑回归也是计算输入特征的加权和（再加上偏置项），但与前者直接输出计算结果不同，后者返回计算结果的逻辑（logistic）。

逻辑回归模型评估概率（向量化形式）：

$\hat{p} = h_\theta(X) = \sigma(\theta^T \cdot X)$

logistic,也被称作logit，记做$\sigma(\cdot)$，是一个sigmoid函数（比如S形函数）。

$\sigma(t) = \frac{1}{1 + e^{-t}}$

$\hat{y} = \left\{\begin{matrix} 0 \ if \ \hat{p}<0.5 \\ 1 \ if \ \hat{p}\geq 0.5 \end{matrix}\right.$

4.6.2 训练和损失函数（Training and Cost Function）

逻辑回归损失函数（log loss） ：

$J(\theta) = -\frac{1}{m}\sum_{i=1}^{m}\{ y^{(i)}log(\hat{p}^{(i)}) + (1 - y^{(i)})log(1 - \hat{p}^{(i)}) \}$

其实，$-J(\theta)$是个极大似然估计等价的。

似然函数定义如下：

$L(\theta) = \prod_{i=1}^n p(Y=y_i|X=x_i) = \prod_{i=1}^n p(x_i)^{y_i}(1-p(x_i))^{1-y_i}$

根据极大似然估计，我们要求出使得$L(\theta)$最大的$\theta$。对等式左右两边取log操作，即可得到跟log loss类似的形式。

log loss求解最小值没有解析解形式，但是该函数是凸函数，可以用梯度下降进行求解。

4.6.3 决策边界（Decision Boundaries）

4.6.4 Softmax Regression

后面这两小节不太重要，以后有时间再补充吧。