第十四章——循环神经网络(Recurrent Neural Networks)(第一部分)
本章共两部分,这是第一部分:
第十四章——循环神经网络(Recurrent Neural Networks)(第一部分)
第十四章——循环神经网络(Recurrent Neural Networks)(第二部分)
这几年提到RNN,一般指Recurrent Neural Networks,至于翻译成循环神经网络还是递归神经网络都可以。wiki上面把Recurrent Neural Networks叫做时间递归神经网络,与之对应的还有一个结构递归神经网络(recursive neural network)。本文讨论的是前者。
RNN是一种可以预测未来(在某种程度上)的神经网络,可以用来分析时间序列数据(比如分析股价,预测买入点和卖出点)。在自动驾驶中,可以预测路线来避免事故。更一般的,它可以任意序列长度作为输入,而不是我们之前模型使用的固定序列长度。例如RNN可以将句子、文档、语音作为输入,进行自动翻译、情感分析、语音转文字。此外,RNN还用于作曲(谷歌Magenta项目作出的the one)、作文、图片自动生成标题。
14.1 周期神经元(Recurrent Neurons)
此前介绍的大部分是前馈神经网络,激活流只有一个方向,从输入层流向输出层。RNN和前馈神经网络很相似,不过也会向后连接。我们来看一个最简单的RNN,只有一个神经元接受输入,只产生一个输出,然后再将输出传递给自己,如图14-1(左侧)。在每一个time step $t$(也叫做一帧),循环神经元接受输入$x_{(t)}$和前一步的输出$y_{(t-1)}$。可以将这一神经元随时间展开,如图14-1(右)。
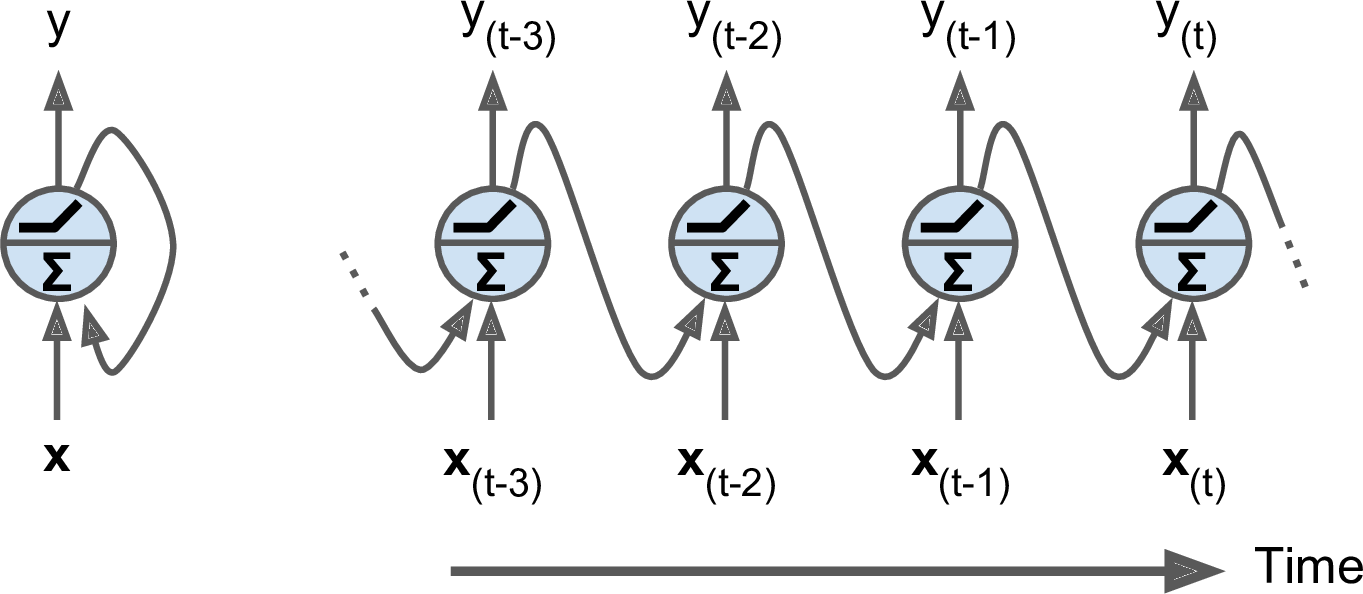
图14-1 一个循环神经元(左),随时间展开(右)
创建一层循环神经元也很简单,只不过在一个time step,输入和输出都是向量,如图14-2。
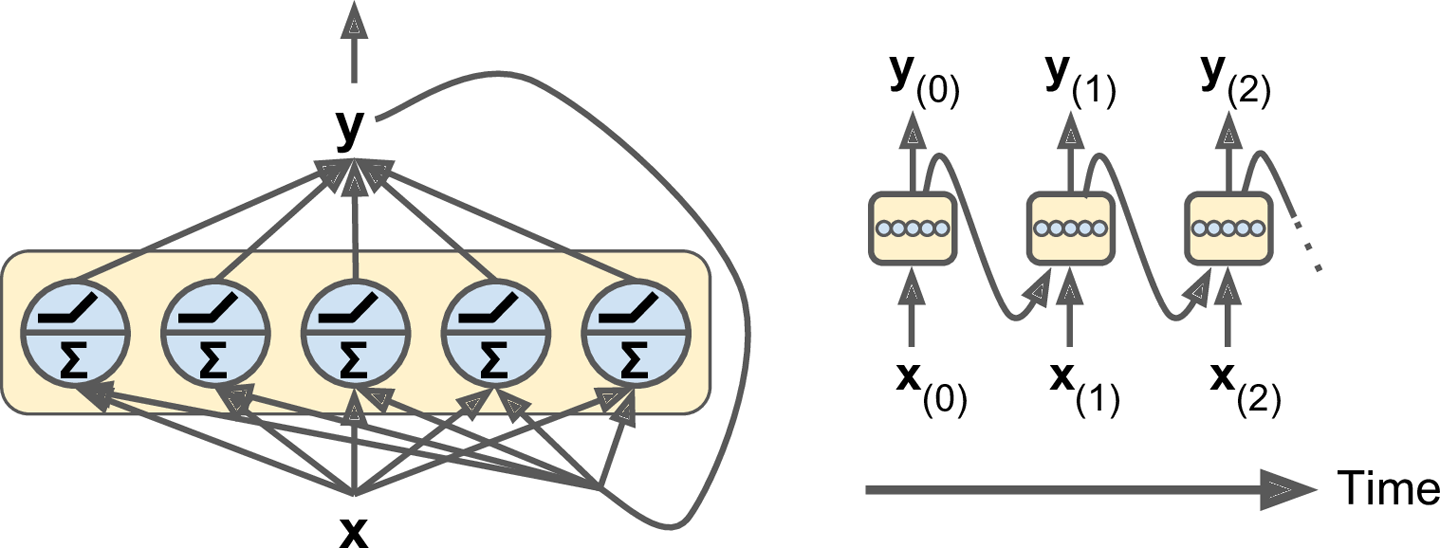
图14-2 一层循环神经元(左),随时间展开(右)
每个神经元都有两套权重:一个用于本层输入$x_{(t)}$,一个用于上层输出$y_{(t-1)}$。我们分别记为$w_x$和$w_y$。
一个循环神经元关于一个实例的输出:
\begin{align*}
y_{(t)} = \phi(x_{(t)}^T \cdot w_x + y_{(t-1)}^T \cdot w_y + b)
\end{align*}
其中,$b$是偏置项,$\phi(\cdot)$是激活函数,比如ReLU(许多研究者更喜欢使用hyperbolic tangent (tanh)作为RNN的激活函数。例如,可以参考Vu Pham等人的Dropout Improves Recurrent Neural Networks for Handwriting Recognition。不过,基于ReLU的RNN也是可以的,比如Quoc V. Le等人的论文A Simple Way to Initialize Recurrent Networks of Rectified Linear Units。)。
一层循环神经元关于整个mini-batch的输出:
\begin{align*}
Y_{(t)} &= \phi(X_{(t)}^T \cdot W_x + Y_{(t-1)}^T \cdot W_y + \textbf{b}) \\
&= \phi([X_{(t)} \quad Y_{(t)}] \cdot W + \textbf{b}) \quad \mbox{with} \quad
W = \begin{bmatrix}
W_x \\
W_y
\end{bmatrix}
\end{align*}
- $Y_{(t)}$是一个$m \times n_{\mbox{neurons}}$矩阵,包含该层在time step $t$关于整个mini-batch实例的输出($m$是mini-batch的实例数,$n_{\mbox{neurons}}$是神经元数量)。
- $X_{(t)}$是一个$m \times n_{\mbox{inputs}}$矩阵,包含该time step $t$所有实例的输入($n_{\mbox{inputs}}$是特征数)。
- $W_x$是一个$n_{\mbox{inputs}} \times n_{\mbox{neurons}}$矩阵,包含当前time step输入到输出的连接权重。
- $W_y$是一个$n_{\mbox{neurons}} \times n_{\mbox{neurons}}$矩阵,包含上个time step输出到当前time step输出的连接权重。
- $W$的形状是$(n_{\mbox{inputs}} + n_{\mbox{neurons}}) \times n_{\mbox{neurons}}$
- $ \textbf{b}$是一个大小为$n_{\mbox{neurons}}$的向量,包含所有神经元的偏置项。
可以看到,$Y_{(t)}$是关于$X_{(t)}$和$Y_{(t-1)}$的函数,$Y_{(t-1)}$又是关于$X_{(t-1)}$和$Y_{(t-2)}$的函数,等等。这使得$Y_{(t)}$其实是关于$X_{(0)},X_{(1)},\cdots ,X_{(t)}$的函数。
14.1.1 Memory Cells
由于神经网络在第$t$个time step的输出是一个关于前$t$个time step所有输入的函数,这可以理解为一种形式的记忆(memory)。神经网络中保存前面时刻状态的部分称为memory cell(或者简单称为cell)。一个单独的周期神经元,或者一层周期神经元,就是一个很基础的cell。随后我们会看到更加复杂和强大的cell。
一般一个cell在时刻$t$(姑且把time step称作时刻把,不然太麻烦)的状态,记做$\textbf{h}_{(t)}$(“h”代表“hidden”),这是一个关于当前时刻输入和前一时刻状态的函数:$\textbf{h}_{(t)} = f(\textbf{h}_{(t-1)}, \textbf{x}_t)$。在$t$时刻的输出,记做$\textbf{y}_{(t)}$,这也是一个关于当前时刻输入和前一时刻状态的函数。在前面讨论的基本cell中,状态和输出是一致的,但在复杂的模型中这是不一致的,如图14-3。
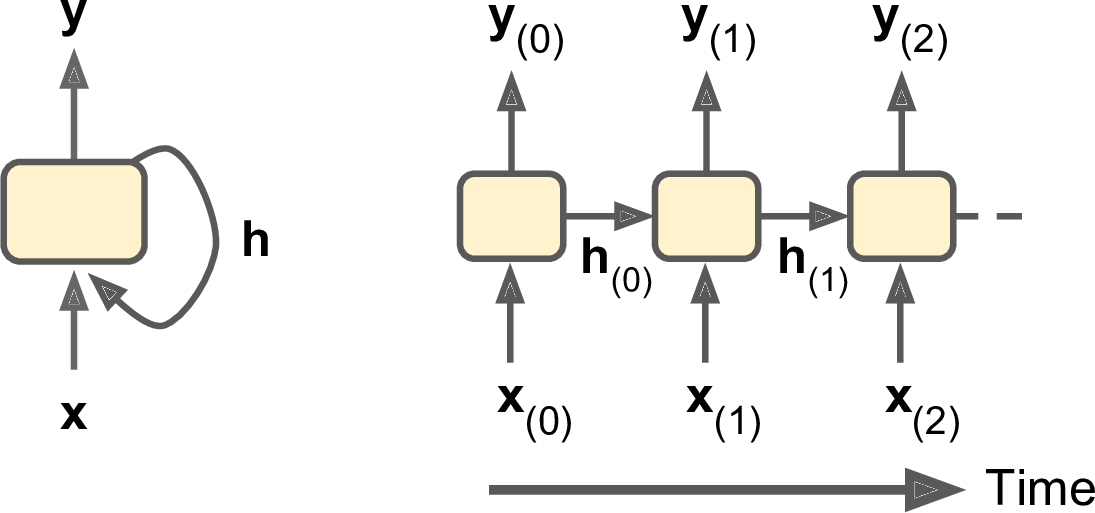
图14-3 一个cell的隐状态可能与它的输出不一致
14.1.2 输入和输出序列
RNN可以一个序列作为输入,再同时输出一个序列(如图14-4左上)。该模型可用于股价预测,输入前$N$天的股价,输出每一天的股价,知道第$N+1$天。每增加一天的输入,就预测下一天的输出。
此外,还可以序列作为输入,忽略除了最后一个之外所有的输出(如图右上)。例如用于情感分析,可以将电影评论作为输入,输出情感分值。
相反的,也可以输入单一的样本,输出一个序列(如图左下)。例如,输入可以是一幅图像,输出是该图像的标题。
最后,右下角的神经网络就是一个翻译系统了。这是序列到向量神经网络(称为encoder)和向量到序列神经网络(称为decoder)的组合。比如,输入可以是一种语言的一句话,encoder将这句话转换为向量表示,decoder再把这个向量表示转换成另一种语言的一句话。这是一个two-step模型,称为Encoder–Decoder,执行翻译任务时,效果比一个序列序列的神经网络好得多。因为原文的最后一个词可能会影响译文的第一个词,所以需要读完全句后再进行翻译。

图14-4 序列到序列(左上),序列到向量(右上),向量到序列(左下),延时的序列到序列(右下)
14.2 基本RNN的TensorFlow实现
首先,我们来实现一个很简单的RNN模型,不使用TensorFlow的任何运算,以便了解底层原理。我们会创建一层有5个训练神经元的RNN(如图14-2),使用tanh激活函数。假设这一RNN有两个时刻,每一时刻的输入是大小为3的向量。下面的代码创建这一RNN,并随时间展开:
n_inputs = 3 n_neurons = 5 X0 = tf.placeholder(tf.float32, [None, n_inputs]) X1 = tf.placeholder(tf.float32, [None, n_inputs]) Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons],dtype=tf.float32)) Wy = tf.Variable(tf.random_normal(shape=[n_neurons,n_neurons],dtype=tf.float32)) b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32)) Y0 = tf.tanh(tf.matmul(X0, Wx) + b) Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b) init = tf.global_variables_initializer()
输入训练数据并运行:
import numpy as np
# Mini-batch: instance 0,instance 1,instance 2,instance 3
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
这一mini-batch有4个实例,每个实例都是包含两个输入的序列。最后Y0_val和Y1_val包含神经网络在两个时刻关于所有实例的输出:
>>> print(Y0_val) # output at t = 0 [[-0.2964572 0.82874775 -0.34216955 -0.75720584 0.19011548] # instance 0 [-0.12842922 0.99981797 0.84704727 -0.99570125 0.38665548] # instance 1 [ 0.04731077 0.99999976 0.99330056 -0.999933 0.55339795] # instance 2 [ 0.70323634 0.99309105 0.99909431 -0.85363263 0.7472108 ]] # instance 3 >>> print(Y1_val) # output at t = 1 [[ 0.51955646 1. 0.99999022 -0.99984968 -0.24616946] # instance 0 [-0.70553327 -0.11918639 0.48885304 0.08917919 -0.26579669] # instance 1 [-0.32477224 0.99996376 0.99933046 -0.99711186 0.10981458] # instance 2 [-0.43738723 0.91517633 0.97817528 -0.91763324 0.11047263]] # instance 3
下面我们看一下,如何使用TensorFlow的RNN运算来实现相同的模型。
14.2.1 随时间静态展开
static_rnn()函数可以创建一个展开的RNN。以下代码可创建与先前相同的模型:
X0 = tf.placeholder(tf.float32, [None, n_inputs]) X1 = tf.placeholder(tf.float32, [None, n_inputs]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, [X0, X1], dtype=tf.float32) Y0, Y1 = output_seqs
首先我们创建了输入占位符,然后是BasicRNNCell,可以将其看作cell工厂。static_rnn()函数调用cell工厂的__call__()函数,为每一时刻创建一个cell,并共享权重和偏置项。static_rnn()返回两个对象,第一个是包含每一时刻输出张量的Python list,另一个是整个网络最终的状态。由于我们使用了最基本的cell,最终的状态其实与第二时刻的输出是一致的。
如果有50个时刻,操作50个输入占位符和50个输出张量实在太繁琐了,需要简化这一过程。下面的代码创建同样的模型,但输出占位符的形状是[None, n_steps, n_inputs],第一个维度是mini-batch的尺寸。X_seqs是一个大小为n_steps的Python list,该list每个元素都是形状为[None, n_inputs]的张量,第一维同样是mini-batch尺寸。为了得到X_seqs,我们首先使用transpose()转置函数交换前两个维度,转置之后时刻就位于第一维度了。然后使用unstack()关于第一维度提取张量list。随后的两行与之前一样。最后再将输出转换成一个形状为[None, n_steps, n_neurons]的张量。
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) X_seqs = tf.unstack(tf.transpose(X, perm=[1, 0, 2])) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, X_seqs, dtype=tf.float32) outputs = tf.transpose(tf.stack(output_seqs), perm=[1, 0, 2])
然后输入训练数据,运行这一网络:
X_batch = np.array([
# t = 0 t = 1
[[0, 1, 2], [9, 8, 7]], # instance 0
[[3, 4, 5], [0, 0, 0]], # instance 1
[[6, 7, 8], [6, 5, 4]], # instance 2
[[9, 0, 1], [3, 2, 1]], # instance 3
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
最终的outputs_val是一个包含所有实例、任一时刻、所有神经元的输出的张量。
然而,这一过程所创建的图仍然是每一时刻包含一个cell。如果有50个时刻,这个图看起来就很丑陋。这就像是写程序而不使用循环(比如Y0=f(0, X0); Y1=f(Y0, X1); Y2=f(Y1, X2); ...;Y50=f(Y49, X50))。图这么大,在反向传播时也很容易造成内存溢出(尤其是运行与GPU内存时),因为需要记录前向传播时每层的所有输出,以便反向传播时计算梯度。
幸运的是,还有更好的解决方案,那就是dynamic_rnn()函数。
14.2.2 随时间动态展开
dynamic_rnn()函数通过while_loop()对cell运算适当地次数。还可以设置swap_memory=True,在反向传播时交换GPU内存和CPU内存来防止OOM错误。更方便的是,它可以接受形状为[None, n_steps, n_inputs])的张量,这就不需要stack,unstack,以及transpose。下面简洁的代码实现了相同的模型:
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
14.2.3 处理变长输入序列
前面我们使用的输入序列都是定长的(都是两个时刻),如果输入序列是变长的呢(比如句子)?这样的话,在调用dynamic_rnn()(或者static_rnn())时,就要使用sequence_length参数了。这是一个1D张量,指明了每个实例的序列长度。例如:
seq_length = tf.placeholder(tf.int32, [None]) [...] outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32, sequence_length=seq_length)
假设我们的第二个实例只有一个时刻的输入,表示该实例张量的第二维需要补零,如下所示:
X_batch = np.array([
# step 0 step 1
[[0, 1, 2], [9, 8, 7]], # instance 0
[[3, 4, 5], [0, 0, 0]], # instance 1 (padded with a zero vector)
[[6, 7, 8], [6, 5, 4]], # instance 2
[[9, 0, 1], [3, 2, 1]], # instance 3
])
seq_length_batch = np.array([2, 1, 2, 2])
with tf.Session() as sess:
init.run()
outputs_val, states_val = sess.run([outputs, states], feed_dict={X: X_batch, seq_length: seq_length_batch})
14.2.4 处理变长输出
如果输出序列是变长的怎么办呢?如果你预先知道输出序列的长度(比如输出序列与输入序列等长),那就可以像先前那样定义一个类似的sequence_length参数。不幸的是,一般无法预测输出的序列长度。这种情况下,最常见的做法是定义一个end-of-sequence token (EOS token)的特殊输出(这将后面自然语言处理的小节进行讨论)。
14.3 训练模型
训练RNN,技巧就是随时间展开,然后应用常规的反向传播(如图14-5)。这一策略称作随时间反向传播(backpropagation through time,BPTT)。
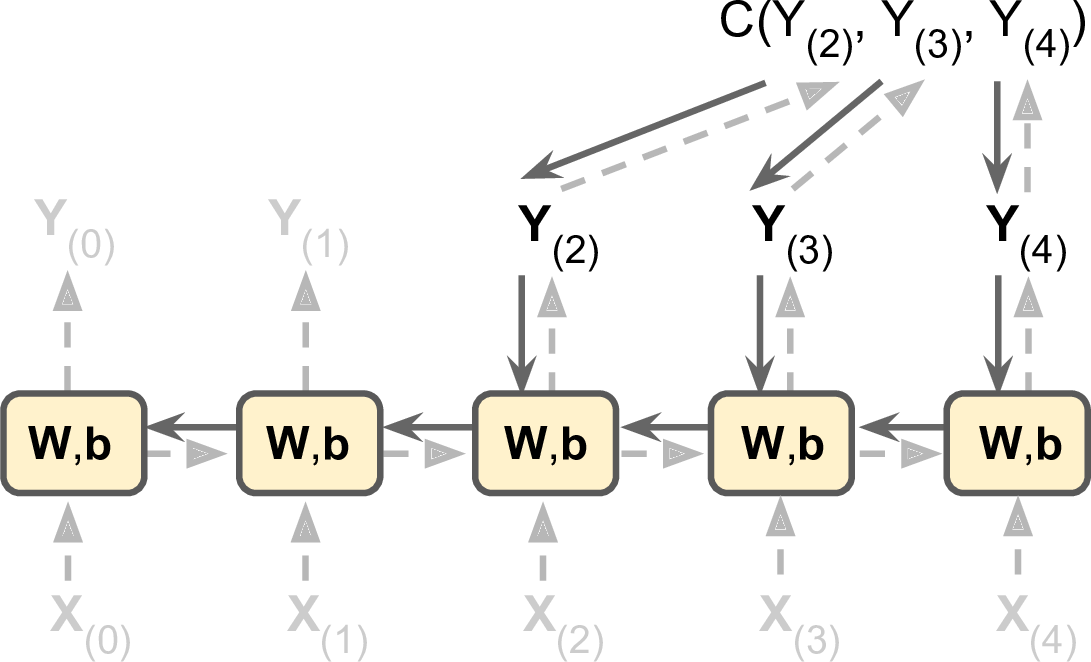
图14-5 随时间反向传播
和常规的反向传播类似,首先展开神经网络前向传播(如上图虚箭头所示),然后使用损失函数$C(Y_{(t_{min})},Y_{(t_{min} + 1)},\cdots,Y_{(t_{max})})$(其中,$t_{min}$、$t_{max}$是第一个和最后一个输出,并且不计算被忽略的输出)对输出进行评估。最后使用梯度更新参数。上图中,损失函数用到了$Y_{(2)}$、$Y_{(3)}$、$Y_{(4)}$三个输出,并没有使用$Y_{(0)}$、$Y_{(1)}$。
14.3.1 训练一个序列分类器
我们来训练一个RNN对MNIST图片进行分类。虽然CNN更适合做图像分类,这里只是使用这个例子来熟悉RNN。可以将MNIST中的每一个图像都看作是28行的序列,每一行又有28个像素点。我们使用150个循环神经元,加上一个全连接层,与输出层连接。最后是softmax层。如图14-6:

图14-6 序列分类器
构建过程是很直接的,并且和第十章的MNIST分类器很相似,只是用RNN的展开替换掉了之前的隐层。与输出层进行全连接的是states张量,只包含最后一个时刻的输出。$y$是目标类别的占位符。
from tensorflow.contrib.layers import fully_connected n_steps = 28 n_inputs = 28 n_neurons = 150 n_outputs = 10 learning_rate = 0.001 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) y = tf.placeholder(tf.int32, [None]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32) logits = fully_connected(states, n_outputs, activation_fn=None) xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) loss = tf.reduce_mean(xentropy) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) correct = tf.nn.in_top_k(logits, y, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) init = tf.global_variables_initializer()
然后加载MNIST数据,并将训练数据转换为[batch_size, n_steps, n_inputs]的形状。
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
y_test = mnist.test.labels
接着是模型的训练,这与第十章是类似的,只不过要改下训练数据的形状:
n_epochs = 100
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
X_batch = X_batch.reshape((-1, n_steps, n_inputs))
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
14.3.2 训练时序数据
这次我们处理时序数据,比如股价、气温、脑电波等等。每一个训练实例都是从时序中随机选出20个时刻(如图14-7左侧)。目标序列与训练序列是相同的,只不是目标序列始终比训练序列晚一个时刻(如图14-7右侧,最下角的实心篮圈,是$t_0$时刻的输入。紧接着的空心篮圈,是$t_1$时刻的输入同时也是$t_0$时刻的目标值。依此类推)。
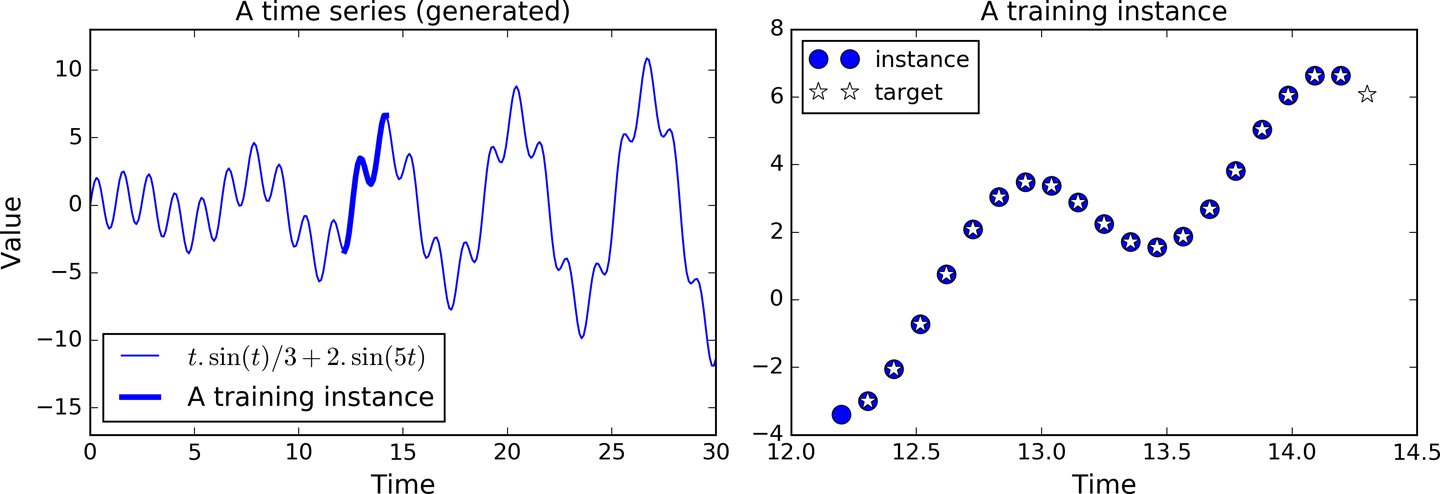
图14-7 时序数据(左),从时序中选出的一个实例(右)
首先,我们来创建RNN。它包含100个循环神经元,并展开为20个时刻。每个时刻的输入只有一个特征。目标值也是同样的20个时刻。代码如下:
n_steps = 20 n_inputs = 1 n_neurons = 100 n_outputs = 1 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) y = tf.placeholder(tf.float32, [None, n_steps, n_outputs]) cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu) outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
一般情况下,每一时刻的输入可能不止一个特征。比如,进行股价预测时,可能还会使用专家评级等信息,来提高预测准确性。我们这里是对模型进行了简化。
在这个模型中,每一时刻都会输出一个大小为100的向量。但我们需要在每一时刻的输出是个标量。最简单的解决方案是使用OutputProjectionWrapper,将cell封装起来。OutputProjectionWrapper在每一时刻的输出之上增加一层全连接的线性神经元(比如不使用激活函数),而且不会影响cell状态。所有这些全连接层共享同样的权重的偏置项(可训练),如图14-8:
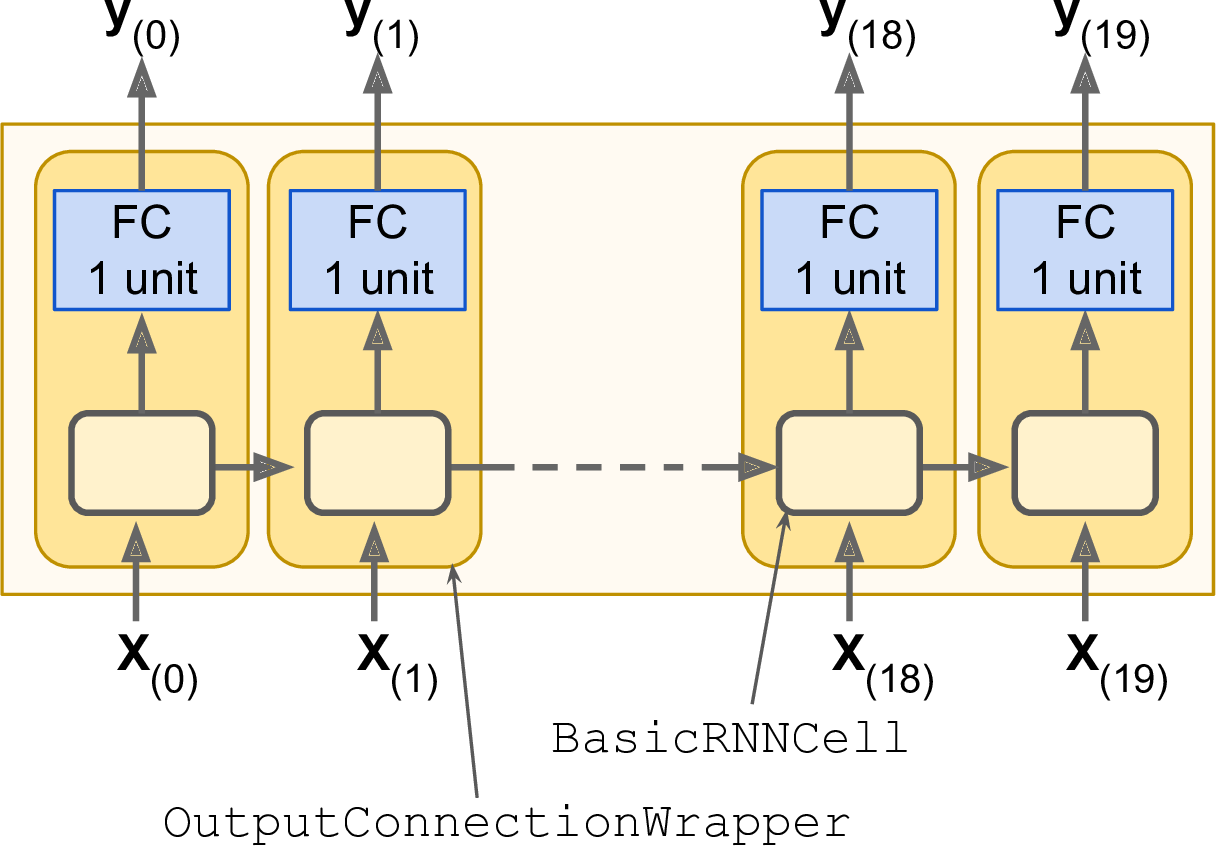
图14-8 使用输出投影的RNN cells
封装cell很容易,简单改变之前的代码即可:
cell = tf.contrib.rnn.OutputProjectionWrapper(
tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu),
output_size=n_outputs)
然后就是定义损失函数,创建Adam优化器,等等:
learning_rate = 0.001 loss = tf.reduce_mean(tf.square(outputs - y)) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) init = tf.global_variables_initializer()
接着就可以执行了:
n_iterations = 10000
batch_size = 50
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = [...] # fetch the next training batch
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
程序的输出如下:
0 MSE: 379.586 100 MSE: 14.58426 200 MSE: 7.14066 300 MSE: 3.98528 400 MSE: 2.00254 [...]
训练好之后,就可以预测了:
X_new = [...] # New sequences
y_pred = sess.run(outputs, feed_dict={X: X_new})
图14-9显示了迭代训练1000次之后的预测序列:
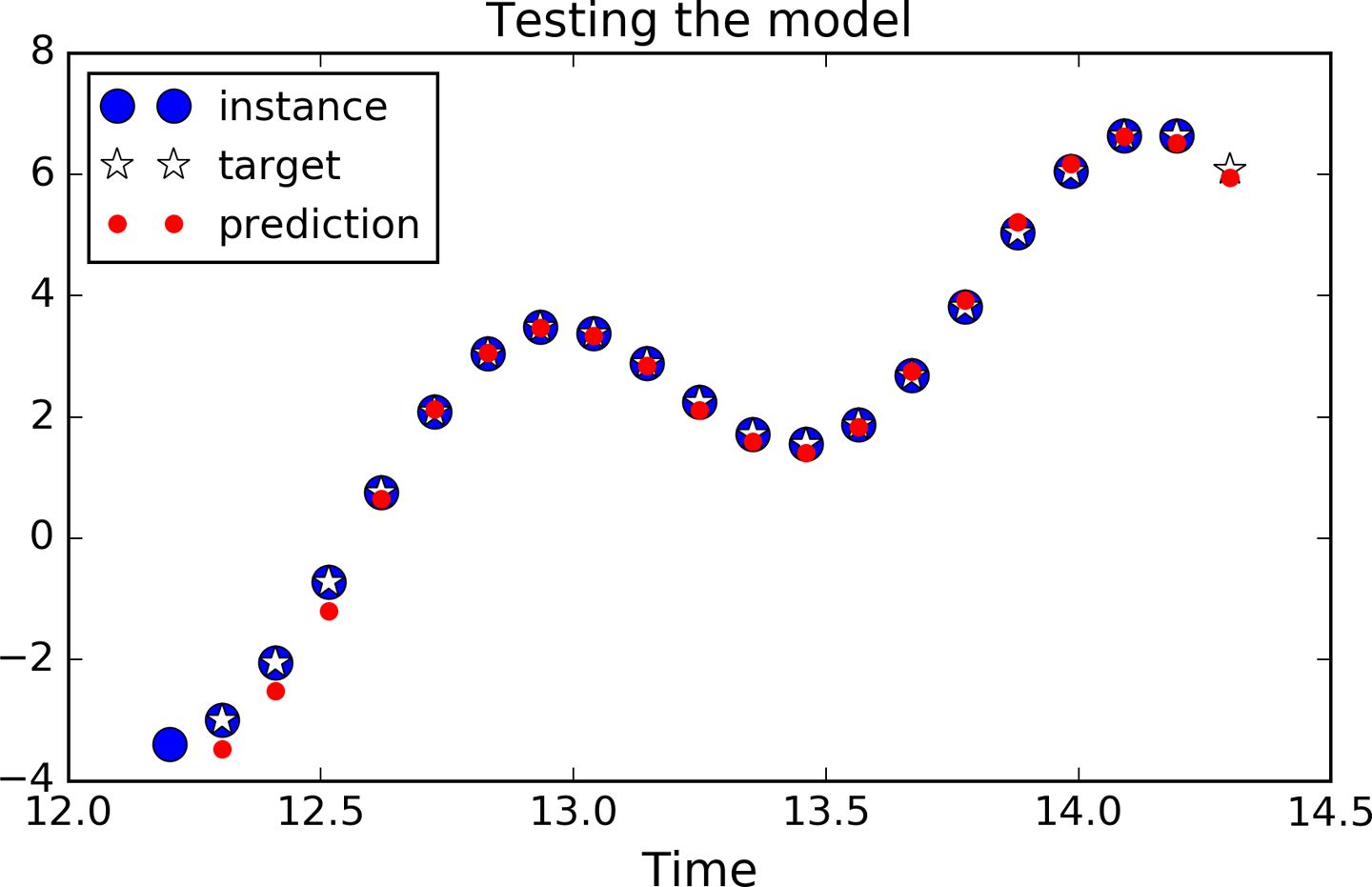
图14-9 时序预测
虽然OutputProjectionWrapper是一种解决方案,但还有一种更高效的方案:首先将RNN的输出从[batch_size, n_steps, n_neurons]转换成[batch_size * n_steps, n_neurons],然后使用一个全连接层给下恰当的输出个数(在我们的例子中,输出1个标量)。 然后再将计算结果从[batch_size * n_steps, n_outputs]转换回[batch_size, n_steps, n_outputs],如图14-10所示:
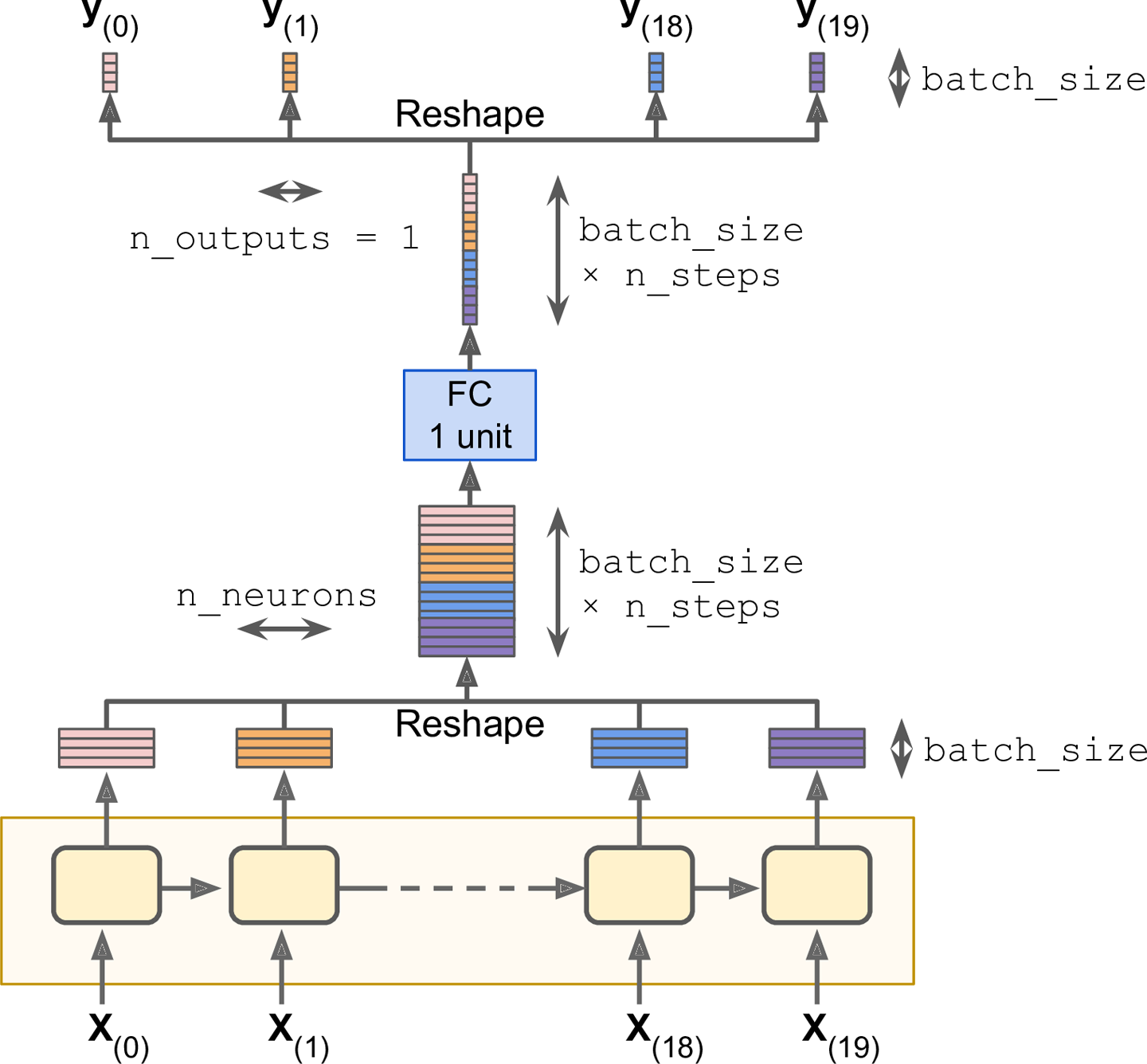
图14-10 堆叠所有输出,应用投影,最后再展开
为实现这一方案,我们首先将代码还原成基本的cell,不再使用OutputProjectionWrapper:
cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu) rnn_outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
然后就是改变RNN输出数据的形状,做映射,再改变回原来的形状:
stacked_rnn_outputs = tf.reshape(rnn_outputs, [-1, n_neurons]) stacked_outputs = fully_connected(stacked_rnn_outputs, n_outputs, activation_fn=None) outputs = tf.reshape(stacked_outputs, [-1, n_steps, n_outputs])
剩下的代码就和之前的一样了。
14.3.3 创造性的RNN
既然我们有了一个可以预测未来的模型,当然也可以用它来产生一些创造性的东西,正如本章开头所提到的。我们只需提供一个包含n_steps个值的种子序列(该种子序列可以全是0), 模型就可以预测下一时刻值。将预测出的值在作为输入,又能得到一个预测值,如此循环下去。代码如下:
sequence = [0.] * n_steps
for iteration in range(300):
X_batch = np.array(sequence[-n_steps:]).reshape(1, n_steps, 1)
y_pred = sess.run(outputs, feed_dict={X: X_batch})
sequence.append(y_pred[0, -1, 0])
可以得到一个新的时序,并且与原来的时序有相似之处,如图14-11
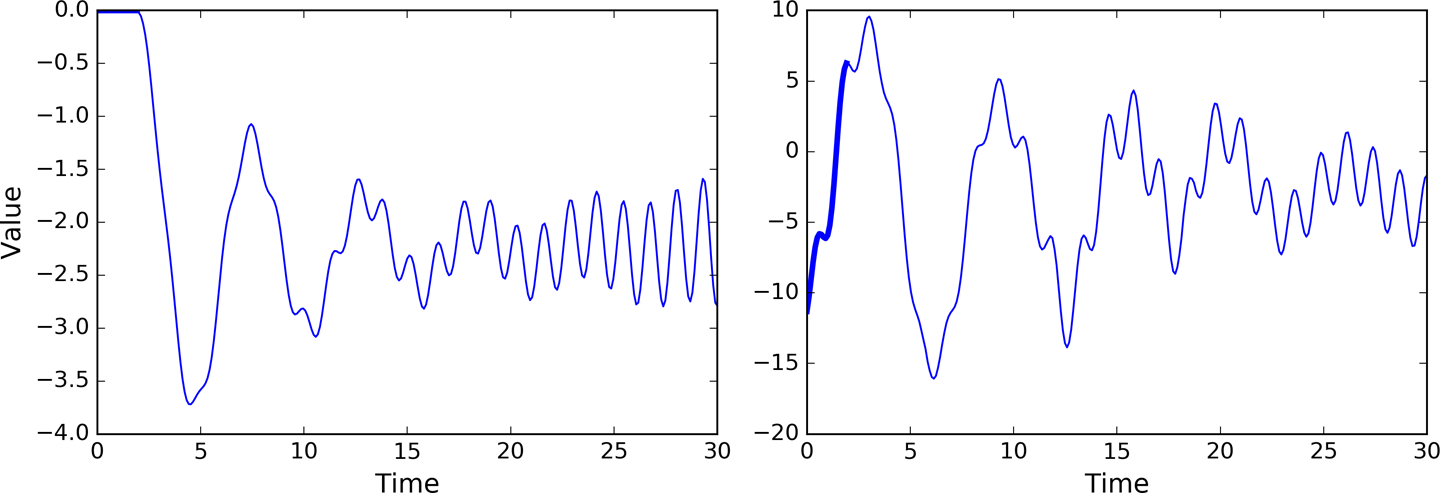
图14-11 创造性的序列,左侧种子是0,右侧种子是一个实例
本文较长,剩下的将写在一篇新的博客中。



