第十章——人工神经网络入门
10.1 从生物到人工神经元(From Biological to Artificial Neurons)
人工神经网络经历了70年的跌宕起伏:深度学习与神经网络:浅谈人工神经网络跌宕起伏七十年。
作者相信这次神经网络浪潮是与众不同的,理由如下:
- 现如今有海量数据用于训练,并且ANNs在处理大规模复杂问题时频繁由于其他ML技术。
- 硬件的性能有了明显的提升,使得训练ANNs的时间可以接受。
- 训练算法有所改进。虽然与1990s相比只是轻微的不同,但却得到了巨大提升。
- ANNs的一些理论上的缺陷,在实践中情况要好得多。例如ANN的损失函数是非凸的,使用梯度下降训练时有可能陷入局部最优解。但这一缺陷在实践中很少见,即使出现,也与全局最优解很接近。
- ANNs似乎进入了“投资——进步”的良性循环。
10.1.1 生物神经元(Biological Neurons)
这需要回忆一下高中生物。https://en.wikipedia.org/wiki/Neuron
神经元通过细长的轴突(Axon)与其它神经元进行联系。轴突的长度可能是细胞体的几倍,也可能是成千上万倍。
虽然单个神经元很简单,但每个神经元都会与数以千计的神经元相联系。数十亿的神经元结合在一起形成巨大的网络,就能进行高度复杂的计算。
10.1.2 逻辑运算神经元(Logical Computations with Neurons)
使用神经元进行或、与、非等运算。
10.1.3 感知机(The Perceptron)
感知机是最简单的ANN架构,由Frank Rosenblatt于1957年发明。它基于被称作linear threshold unit (LTU)的人工神经元。LTU首先计算输入值的加权和($z = w_1x_1 + w_2x_2 + \cdots + w_nx_n = W^T \cdot X$),然后对$z$应用一个阶梯函数(step function):
$h_W(x) = step(z) = step(W^T \cdot X)$。
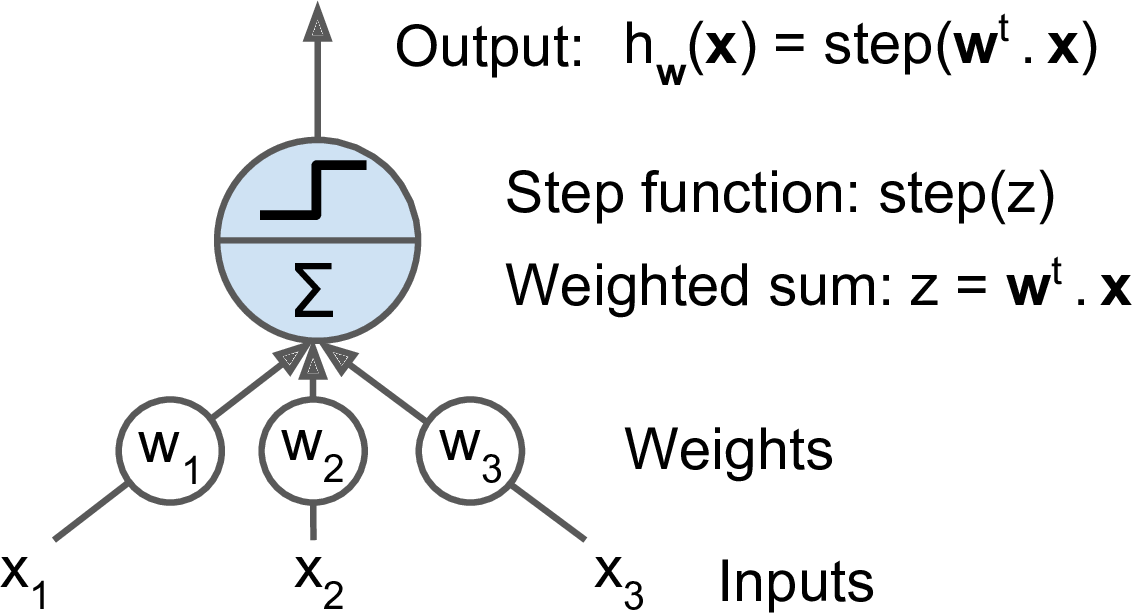
图10-4. LTU
感知机常用阶梯函数:
\begin{align*}
\mbox{heaviside}(z) = \left\{\begin{matrix}
0 \quad \mbox{if} \quad z < 0 \\
1 \quad \mbox{if} \quad z \geq 0
\end{matrix}\right.
\end{align*}
\begin{align*}
\mbox{sgn}(z) = \left\{\begin{matrix}
-1 &\quad \mbox{if} \quad z < 0 \\
0 &\quad \mbox{if} \quad z = 0 \\
+1 &\quad \mbox{if} \quad z < 0
\end{matrix}\right.
\end{align*}
感知机学习规则:
$w_{i,j}^{\mbox{(next step)}} = w_{i,j} + \eta(y_j - \hat{y}_j)x_i$
(书中在括号里面写的是$\hat{y}_j - y_j$,这是不对的,可参考https://en.wikipedia.org/wiki/Perceptron里面的算法步骤)
其中:
- $w_{i,j}$是第i个输入神经元到第j个输出神经元的权重。
- $x_i$是当前训练样本的第i个值。
- $\hat{y}_j$是当前训练样本预测值的第j个输出。
- $y_j$是当前训练样本的第j个标签。
- $\eta$是学习率
感知机的决策边界是线性的,不能学习复杂模式,比如不能解决异或问题。但是可以通过多层感知机解决。
10.1.4 多层感知机和反向传播
可以参考:反向传播算法
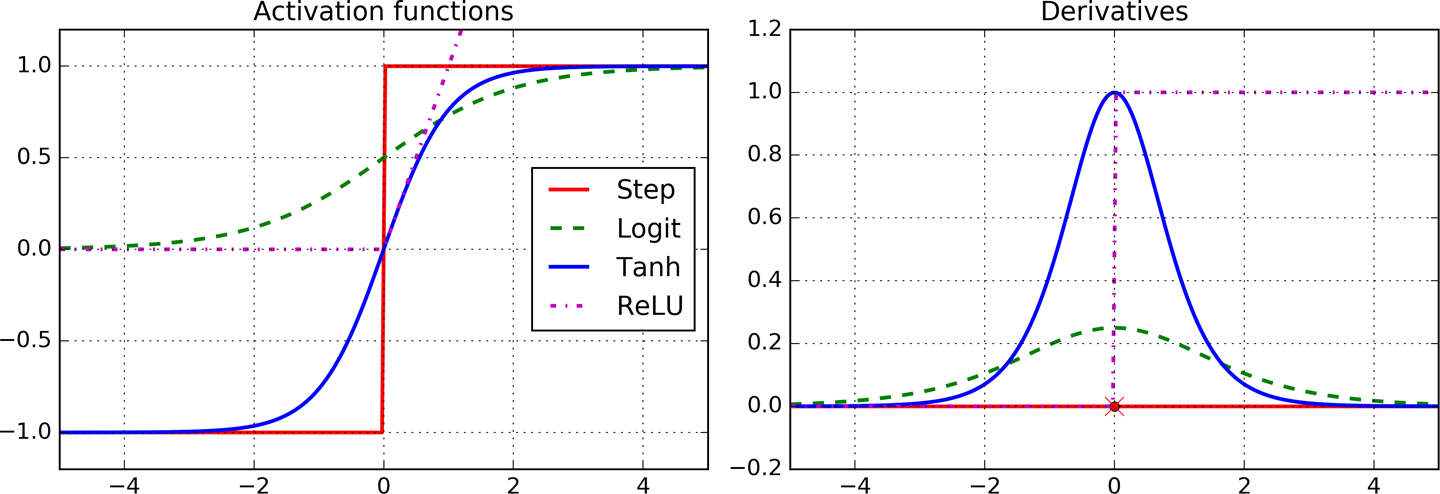
图10-8 常见激活函数及其导数
10.2 使用TensorFlow高级API训练MLP
以下代码训练一个DNN用于分类,包括两个隐层(一个有300神经元,一个有100神经元)和一个包含10个神经元的softmax输出层。
import tensorflow as tf feature_columns = tf.contrib.learn.infer_real_valued_columns_from_input(X_train) dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300, 100], n_classes=10, feature_columns=feature_columns) dnn_clf.fit(x=X_train, y=y_train, batch_size=50, steps=40000)
如果使用MNIST数据集(需要进行归一下,scale)进行训练,可以达到98.1%的正确率。
>>> from sklearn.metrics import accuracy_score >>> y_pred = list(dnn_clf.predict(X_test)) >>> accuracy_score(y_test, y_pred) 0.98180000000000001
模型评估:
>>> dnn_clf.evaluate(X_test, y_test)
{'accuracy': 0.98180002, 'global_step': 40000, 'loss': 0.073678359}
10.3 Training a DNN Using Plain TensorFlow
使用低级被python api训练DNN,代码位置。
10.4 超参数调整
神经网络的灵活性也是其一大缺点:需要调整的超参数太多。无论使用任何网络拓扑结构,都可以调整层数、每层神经元数、每层激活函数种类、权重初始化的逻辑,等等。
当然,可以使用网格搜索和交叉验证来寻找合适的超参数。但是现在有太多的超参数,需要大量的时间在超参数空间中探索。最好的方法是使用随机搜索,这在第二章也有介绍。还有一种选择是使用类似Oscar的工具,其实现了复杂的算法帮助我们快速寻找合适的超参数。
下面将谈一下一些超参数使用哪些值是合理的。
10.4.1 隐层数
对于很多问题,使用一个隐层就能得到不错的结果。已经证明,对于只有一个隐层的MLP,只要提供足够的神经元,就能对最复杂的函数建模。长期以来,这一事实使得研究者确信,不需要研究更深层的神经网络。但他们忽视了深层网络比浅层网络具有更高的参数效率(parameter efficiency):前者可以使用更少的参数模拟复杂函数,这就可以更快速地训练。
为了理解为什么会这样,假设你要使用画图软件绘制一个森林,但是复制/粘贴被禁用。这就要单独地绘制每一棵树,每一个分支,每一片树叶。但如果可以使用复制粘贴,那将可以迅速完成整个森林。真实世界的数据同样具有分层的结构,DNNs正好可以利用这一事实:低级隐层模拟低级结构(比如线性切分不同的形状和方向),中间的隐层结合低级结构来模拟中级结构(比如方形,圆形),中级隐层和输出层结合中级结构来模拟高级结构(比如人脸)。
总之,对于许多问题,都可以从一两个隐层开始训练。对付复杂问题,可以逐步增加隐层,直到过拟合。特别复杂的问题,比如图片分类和语音识别,一般需要几十层(或者上百层,但不是全连接,这将在第十三章介绍)。但是,一般不需要从头开始训练这种网络:可以复用训练好的任务相似的网络,这可以节省大量的训练时间和训练数据(这将在第十一章介绍)。
10.4.2 每个隐层神经元数
很明显,输入层和输出层的神经元数量由具体的分类任务决定。比如,MNIST任务需要$28 \times 28 = 784$个输入神经元和10个输出神经元。对于隐层,以往一个通常的做法是使其呈漏斗形,神经元数量逐层减少。其理论依据是,低级别的特征会被合并到高级别特征中。但是现如今,这一经验不再是通常的选择,你可以在每个隐层使用相同数量的神经元。和调整隐层数量相同,调整神经元数量时,也可以逐步增加知道过拟合。一般情况下,调整隐层数量比调整每层神经元数量更划算一些。
不幸的是,寻找合适数目的神经元,依然是a black art。一个简单的做法是,使用比实际需要更多的隐层数和神经元数量,然后early stopping防止过拟合(还有其他的正则化技术,尤其是dropout,将在第十一章介绍)。这被称为拉伸裤子(stretch pants)技术:与其浪费时间寻找恰好合适的尺寸,不如选择更长的裤子,然后裁剪到合适尺寸(这是在Vincent Vanhoucke的深度学习课程中提到的,免费的哦)。
10.4.3 激活函数
大多数情况下隐层使用ReLU(或其变种)就可以了。它比别的激活函数更快,and Gradient Descent does not get stuck as much on plateaus,thanks to the fact that it does not saturate for large input values (as opposed to the logistic function or the hyperbolic tangent function, which saturate at 1)。(这句话没看懂)
对于输出层,softmax常用于分类问题,而回归问题可以简单地不使用激活函数。



