第三章——分类(Classification)
3.1 MNIST
本章介绍分类,使用MNIST数据集。该数据集包含七万个手写数字图片。使用Scikit-Learn函数即可下载该数据集:
>>> from sklearn.datasets import fetch_mldata
>>> mnist = fetch_mldata('MNIST original')
>>> X, y = mnist["data"], mnist["target"]
>>> X.shape
(70000, 784)
>>> y.shape
(70000,)
70000张图片,每张图片有784个特征,代表28*28个像素点。每个像素点取值从0(白)到255(黑)。并且前60000张是训练集,后10000张是测试集。
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
训练集是按照数字的顺序进行排序的,我们需要将顺序打乱,这可以保证交叉验证的k个部分是一致的(我们不希望某一部分缺少一些数字)。此外,一些算法对训练集的顺序是敏感的,在一行出现很多相似样本时会表现很差。打算训练集就是为了防止这一情况发生。有时候打乱顺序是不明智的——例如,处理的是时序数据(time series data,比如股价、天气),这将在后面章节讨论。
import numpy as np # 打乱训练集数据顺序 shuffle_index = np.random.permutation(60000) X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
3.2 训练二元分类器(Training a Binary Classifier)
首先将问题简化,训练一个二元分类器。比如只判断图像是5或者不是5。目标向量可通过如下代码创建:
y_train_5 = (y_train == 5) # True for all 5s, False for all other digits. y_test_5 = (y_test == 5)
作者选择了随机梯度下降(Stochastic Gradient Descent,SGD。梯度下降可参考:梯度下降求解线性回归)分类器,Scikit-Learn’s SGDClassifier。
3.3 性能评估(Performance Measures)
3.3.1 交叉验证计算准确率(Measuring Accuracy Using Cross-Validation)
>>> from sklearn.model_selection import cross_val_score >>> cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy") array([ 0.9502 , 0.96565, 0.96495])
得了95%以上的正确率,这似乎很不错了。事实上,我们可以定义一个很弱智的分类器,该分类器把所有图像都识别为不是5,该分类器也能有90%的正确率,因为5的图像只占总数的10%。这就很尴尬了。
因此,对于分类问题来说,准确率通常不是最好的衡量指标,特别是处理倾斜数据集时(skewed datasets,例如一些类别的频率明显高于其它类别)。
3.3.2 混淆矩阵(Confusion Matrix)
>>> from sklearn.model_selection import cross_val_predict >>> y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) >>> from sklearn.metrics import confusion_matrix >>> confusion_matrix(y_train_5, y_train_pred) array([[53272, 1307], [ 1077, 4344]])
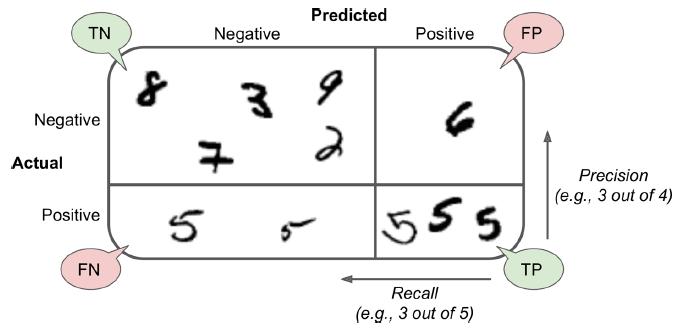
每行代表真实类别,每列代表预测类别。第一行是真实值为非5的图像(负类别,the negative class):53,272个样本正确分类为非5(这被称作true negatives,TN),其余的1,307个被错误分类为5(false positives,FP)。第二行是真实值为5的图像:1,077个图片被错误分类为非5(false negatives),剩下的4,344个被正确分类为5(true positives)。
定义精度(precision)和召回率(recall):
\begin{align*}
precision &= \frac{TP}{TP + FP} \\
recall &= \frac{TP}{TP + FN} \\
\end{align*}
3.2.3 精度和召回率(Precision and Recall)
>>> from sklearn.metrics import precision_score, recall_score >>> precision_score(y_train_5, y_pred) # == 4344 / (4344 + 1307) 0.76871350203503808 >>> recall_score(y_train_5, y_train_pred) # == 4344 / (4344 + 1077) 0.79136690647482011
现在可以看出,我们的分类是表现的并不好,尽管准确率(accuracy)是95%以上。当分类器认为一个图像是5时,这只有不到77%的情况下是正确的。此外,只检测大了79%的5。
可以将精度和召回率组合成一个被称为$F_1$值的指标,这在比较两个分类器时很方便。$F_1$值是精度和召回率的调和平均数(harmonic mean)。普通的平均数处理所有值都是均等的,调和平均数给予小值更高的权重。只有在精度和召回率都比较高的情况下,才会得到比较高的$F_1$值。
\begin{align*}
F_1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} = 2 \times \frac{precision \times recall}{precision + recall} = \frac{TP}{TP + \frac{FN + FP}{2}}
\end{align*}
>>> from sklearn.metrics import f1_score >>> f1_score(y_train_5, y_pred) 0.78468208092485547
精度和召回率相近的分类器,倾向于得到较高的$F_1$值。但有时候我们更关心精度,有时候真正看重的是召回率。
例如,训练一个视频分类器,检测出对儿童安全的视频,这就需要宁缺(低召回率)毋滥(高精度)了。
再比如,你的分类器时检测扒手的,为了一个坏人都不放过(高召回率),即使精度低一些也可以接受。
不幸的是,鱼和熊掌不可兼得:增大召回率造成精度减小,反之亦然。这被称为精度/召回率权衡(precision/recall tradeoff)。
3.2.4 精度/召回率权衡(precision/recall tradeoff)
首先说明一下SGDClassifier是怎么做分类决策的。对于每一个实例,它都会通过决策函数计算一个分支,如果该分值高于阈值, 就预测该实例为正样本,反之预测为负样本。
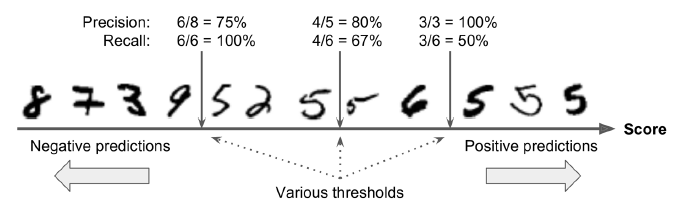
图3-3.决策阈值和精度/召回率权衡
虽然Scikit-Learn并不允许直接修改阈值,但可以获取用于预测的决策分值(decision scores)。
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
plt.xlabel("Threshold")
plt.legend(loc="upper left")
plt.ylim([0, 1])
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()
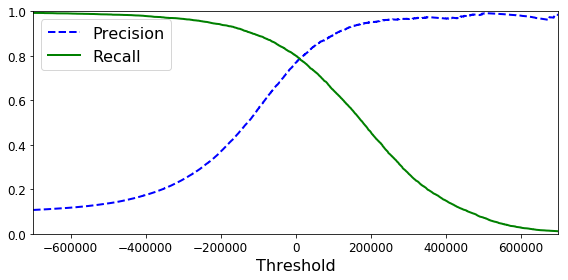
不同阈值下的精度和召回率
另外一个权衡精度和召回率的方式是直接画出二者图像:

可以看出,在80%召回率附近,精度开始快速下降。可以在这一下降之前对精度和召回率做一权衡,比如选择60%的召回率。当然,这取决于具体的项目。
如果有人说:让我们达到99%的精度。你应该问,基于什么样的召回率?
如果一个分类器召回率特别低,即使它的精度很高,那也没什么用。
3.2.5 ROC
ROC(receiver operating characteristic)曲线是另一个二分类器的常用工具。它和精度/召回率曲线类似。不同之处在于,ROC曲线画出的是不同FPR(false positive rate)下的TPR(true positive rate,这是召回率的别名)。
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plot_roc_curve(fpr, tpr)
plt.show()

图3-6.ROC曲线
这也需要进行权衡:召回率(TPR)越高,分类器就会产生越多的错误正样本(FPR)。
分类器好坏的一个度量方式是AUC(area under the curve)。一个完美的分类器,ROC AUC等于1。而一个完全随机的分类器,ROC AUC等于0.5。
由于ROC曲线和精度/召回率(precision/recall,PR)曲线是如此的相似, 或许存在困惑该如何选取。一般来说,如果正样本是稀少的,或者相较于错误的负样本,你更关心错误的正样本,那就应该选择PR曲线。反之,选择ROC曲线。例如,观察一下先前的ROC曲线(包括ROC AUC分值),那可能觉得分类器已经相当好了。但这主要是因为负样本(非5)明显多于正样本(5)。与之相反,PR曲线显示出我们的分类器明显还有提升的空间(曲线可以更靠近右上角)。
3.3 多标签分类(Multilabel Classification)
3.4 Multioutput Classification



 浙公网安备 33010602011771号
浙公网安备 33010602011771号