高级词向量表示
本文是在上文自然语言处理——词的表示基础上,引入一个更先进的词向量模型GloVe。然后介绍如何内在和外在地评估词向量。
1 Global Vectors for Word Representation (GloVe)
1.1 和先前方法的比较
上文介绍了两类获取词向量的方法。第一类基于计数和矩阵分解,比如潜在语义分析(Latent Semantic Analysis,LSA)、语义存储模型(Hyperspace Analogue to Language,HAL)。这类方法有效地利用全局统计信息,善于捕捉词汇间的相似之处,但是对诸如词类比(比如:北京之于中国,相当于东京之于日本。其实就是对对联嘛:天对地,雨对风,大陆对长空。山花对海树,赤日对苍穹。现成的训练语料^_^)的任务就无能为力了,说明这是欠佳的向量空间结构。另一类基于浅窗口(窗口一般是5到10),通过在局部上下文窗口中做预测来学习词向量(比如skip-gram和CBOW)。这类方法处理词汇相似性之外,还能捕捉到复杂的语言模式,但并不能利用全局的共现统计信息。
相比之下,二者的优点GloVe兼而有之。由于包含一个基于词与词全局共现次数的最小二乘模型,因此更有效地利用了全局统计信息。该模型生成的词向量空间具有更丰富的子结构。它在词类比的任务中达到了最高的水准,在一些词相似性任务中也胜过了其他的模型。
简而言之,GloVe利用全局统计信息预测词$j$出现在词$i$的上下文环境中的概率。
1.2 共现矩阵
- $X$:词与词的共现矩阵。
- $X_{ij}$:词$j$出现在词$i$的上下文环境中的次数。
- $X_i = \sum_k X_{ik}$:在词$i$的上下文环境中出现过的所有词的总数。
- $P_{ij} = P(w_j|w_i) = \frac{X_{ij}}{X_i}$:词$j$出现在词$i$的上下文环境中的概率。
计算该矩阵需要对整个语料进行一次扫描。对于较大的语料集,这是耗时的,不过也是一劳永逸的。
1.3 最小二乘目标函数
回忆一下,在skip-gram模型中,我们使用softmax来计算词$j$出现在词$i$的上下文环境中的概率:
\begin{align*}
Q_{ij} = \frac{\exp(\vec{u}_j^T\vec{v}_i)}{\sum_{w=1}^{W} \exp(\vec{u}_w^T\vec{v}_i)}
\end{align*}
可以通过在线的,随机的方式进行训练(这里是随机梯度下降的意思吧。这种模型可用于在线学习,从而与时俱进,对于新语料、新词汇的加入很友好,这点要优于GloVe)。但是其中包含的全局交叉熵损失可通过如下方式计算:
\begin{align*}
J = -\sum_{i \in corpus} \sum_{j \in context(i)} \log(Q_{ij})
\end{align*}
由于同样的词$i$和词$j$可能会在语料中共现多次,首先将同样的$i$和$j$整合到一起:
\begin{align*}
J = -\sum_{i=1}^{W} \sum_{j=1}^{W} X_{ij} \log(Q_{ij})
\end{align*}
交叉熵损失有一个明显的缺陷:需要对$Q$的分布进行适当的规范化(也就是说,$Q$必须是个概率空间,$\sum Q = 1$),而这涉及到对所有的词汇求和,计算量巨大(其中,上一节的3.4 Negative Sampling和3.5 分层Softmax也给出了针对这一问题的解决方案)。为了避免这一问题,我们使用最小二乘目标函数,并抛弃掉需要规范化的因子$Q$:
\begin{align*}
\hat{j} = \sum_{i=1}^{W} \sum_{j=1}^{W}X_i(\hat{P}_{ij} - \hat{Q}_{ij})^2
\end{align*}
其中,$\hat{P}_{ij} = X_{ij}$和$\hat{Q}_{ij} = \exp(\vec{u}_j^T\vec{v}_i)$是未规范化分布(unnormalized distributions,可以参考What is an unnormalized measure in probability theory?以及Unnormalized probability: A different view of statistical mechanics)。这一公式有引入了新的问题:$X_{ij}$的值往往都很大,导致难以优化。一个有效的解决方案是取对数:
\begin{align*}
\hat{j} &= \sum_{i=1}^{W} \sum_{j=1}^{W}X_i(\log(\hat{P}_{ij}) - \log(\hat{Q}_{ij}))^2 \\
&= \sum_{i=1}^{W} \sum_{j=1}^{W} X_i(\vec{u}_j^T\vec{v}_i - \log(X_{ij}))^2
\end{align*}
此外,根据观察发现,我们并不能保证权重因子$X_i$是最优的。因此,我们使用一个更一般的权重函数,可以根据上下文词汇自由选择:
\begin{align*}
\hat{j} &= \sum_{i=1}^{W} \sum_{j=1}^{W} f(X_{ij})(\vec{u}_j^T\vec{v}_i - \log(X_{ij}))^2
\end{align*}
2 词向量评估
到目前为止,我们已经介绍了诸如Word2Vec、GloVe的方法,来训练和发现自然语言词语在语义空间潜在的词向量表示。接下来,我们介绍如何评估这些由不同模型所产生的词向量。
2.1 内在评估
内在评估就是通过明确的中间子任务(一个媒介任务,并不是最终的任务,比如词汇类比的表现)对各种技术产生的词向量进行评估。这些子任务一般都很简单,并且可以很快得到计算,因此帮助我们理解生成这些词向量的系统。内在评估方法一般都会返回一个数字,来说明词向量在这些子任务中的表现。
使用内在评估方法的动机是什么呢?比如我们的最终目标是创建一个以词向量为输入的问答系统。可以用如下方法训练一个机器学习系统:
- 以词作为输入
- 将词转换成词向量
- 使用词向量作为一个机器学习系统的输入
- 将输出的词向量映射为相应的自然语言词汇
- 将词作为答案输出
在构建对话系统的过程中,需要创建尽可能理想的词向量表示,因为这会用于下游的子系统(比如一个深度神经网络)。为达到这一目的,需要调整Word2Vec子系统中的许多超参数(比如词向量的维度)。最理想的方法是,每调整一个Word2Vec的超参数,就对整个系统重新训练一次。但这在工程实践中是不可能的,因为下游的机器学习系统(第3步)很可能是个深度神经网络,具有成千上万个参数,训练起来很费时间。在这种情形下,就需要一个内在的评估手段,来鉴别所生成词向量的优劣。
简而言之,内在评估有如下特点:
- 在一个明确的中间任务上评估
- 可以快速算得结果
- 有助于理解子系统(也就是生成词向量的系统)
- 和最终的任务正相关
2.2 外在的评估
- 使用真实的任务进行评估
- 计算时间较长
- 不容易确定,到底是哪个子系统出了问题,或者交叉影响
- 替换掉一个子系统,看一下性能是否提升。
2.3 内在评估案例:词向量类比
在词向量类比中,首先给出如下不完整的类比形式:
a : b : : c : ?
然后内在评估系统求得使下面余弦相似度最大的词向量:
\begin{align*}
d = \mathop{\arg\max}\limits_{i} \frac{(x_b - x_a + x_c)^T x_i}{\left \| x_b - x_a + x_c \right \|}
\end{align*}
这一度量标准有一个直观上的解释。理想的情况下,我们希望$x_b - x_a = x_d - x_c$(比如,后 - 王 = 女演员 - 男演员)。
考虑如下形式的词类比:
城市1:所在州1::城市2:所在州2
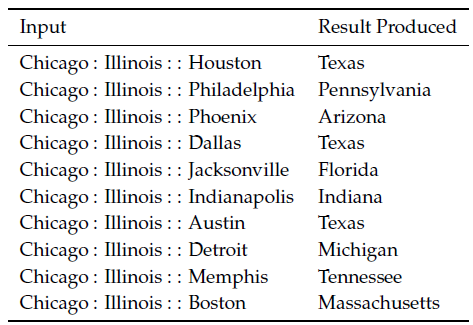
表1 语义上的词向量类比
由于美国大量的城市/城镇/乡村存在同名的情况(其实中国也一样。比如吉林省市同名,广州市和贵阳市都有一个白云区,全国有无数个城关镇),所以有些答案可能不唯一。例如,全美至少有10个地方叫做Phoenix,因此Arizona不需要是唯一的正确答案。我们再来看另一个形式的类比:
首都1:国家1::首都2:国家2
在很多情况下,以上形式产生的都是该国家最近的首都。这也有一个问题,比如,在1997年以前,哈萨克斯坦的首都是阿拉木图(现在是阿斯塔纳)。因此,如果语料过时的话,我们会得到不同的答案。
上面两个例子,都是词向量在语义上的类比,当然也可以在语法上类比。例如,形容词与其最高级的类比:
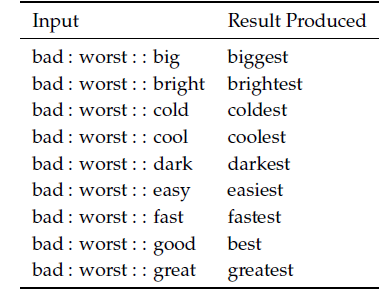
表2 语法上的词向量类比
2.4 内在评估调整案例
可供内在评估技术调整的几个词向量模型超参数:
- 词向量维度
- 语料大小
- 语料来源/种类
- 上下文窗口大小
- 上下文对称性

表3 不同模型在不同语料和超参数下的表现
从表3中,我们可以总结出3点主要的信息:
- 效果严重依赖于所使用的模型。
- 大语料集可以取得刚好的效果。
- 词向量维度过高或过低,效果都不理想。维度过低捕捉的信息不全,从而欠拟合。维度过高,容易捕捉到语料中的噪声,从而过拟合。
实现细节:窗口选择8时,GloVe的效果最好。
以下三幅图分布是对训练次数、语料规模、词向量维度和窗口大小的调整:
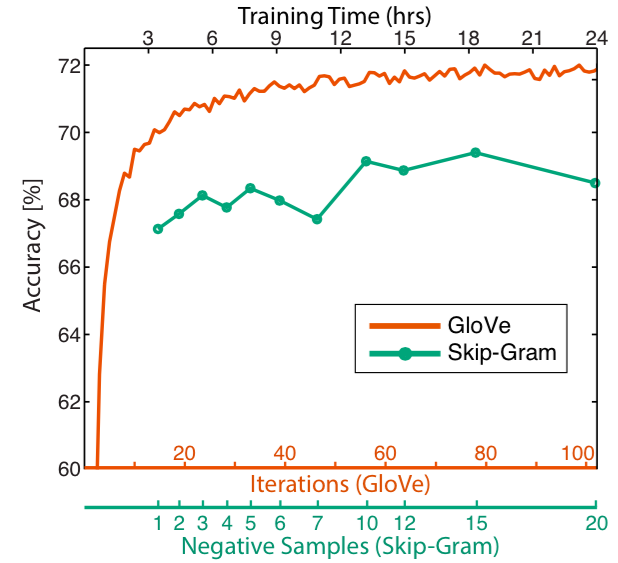
图1 迭代次数对性能的影响
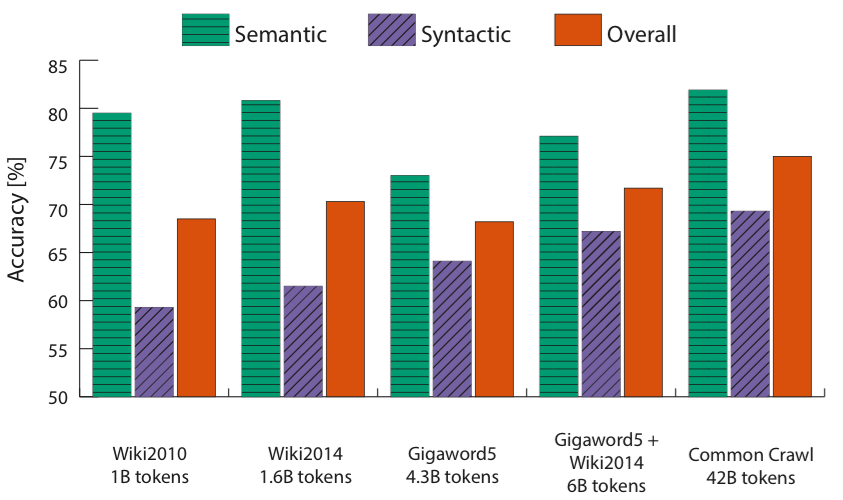
图2 语料规模如何影响词向量的性能
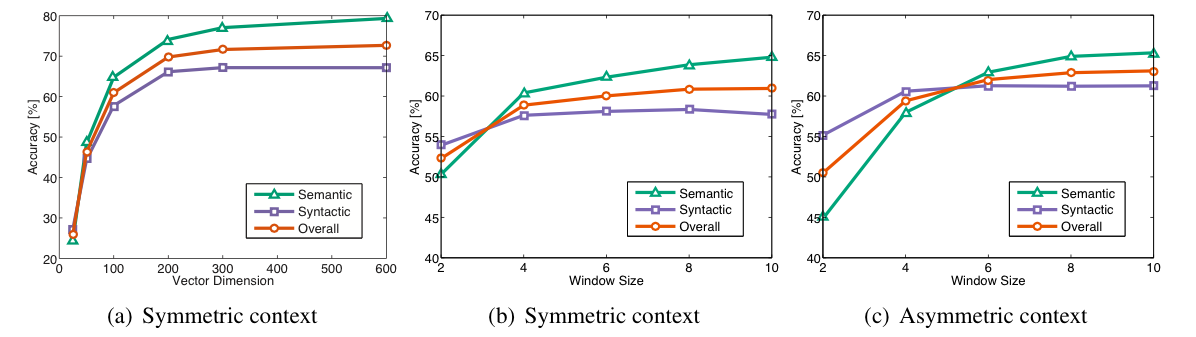
图3 词向量维度、窗口大小对GloVe性能的影响
2.5 内在评估案例:相似性评估
另一个内在评估方法是,人工标注两个词之间的相似度(在一定范围内,比如0-1),然后和两个词向量之间的余弦相似度进行比较。
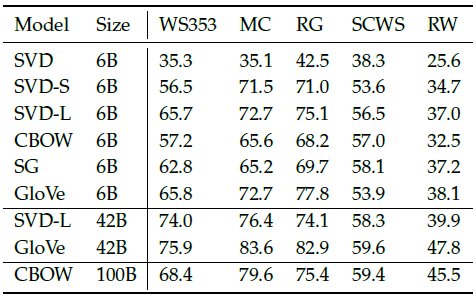
表4 通过相似度评估不同模型的性能
3 外在任务的训练
下面讨论使用词向量处理真实的外在任务的一般方法。
3.1 问题界定
大多数NLP任务都可以被定义为分类任务。例如,给一个句子,分析其情感是积极的还是消极的。类似的,对于命名实体识别(named-entity recognition,NER), 给出一个上下文环境和一个中心词,我们需要将中心词归为很多类别中的一个。例如,"Jim bought 300 shares of Acme Corp. in 2006",分类后的输出结果为:"[Jim]Person bought 300 shares of [Acme Corp.]Organization in [2006]Time."。对于这类问题,我们一般都是从如下形式的训练集开始:
\begin{align*}
\{ x^{(i)}, y^{(i)} \}_1^N
\end{align*}
其中,$x^{(i)}$是一个d维词向量。$ y^{(i)}$是代表某个类别的one-hot向量(比如情感信息,别的词语,命名实体,买入/卖出信号,等等)。
在一般的机器学习任务中,我们通常都是使用输入数据和目标标签,通过一些优化技术(比如梯度下降,L-BFGS,牛顿法,等等)来训练模型。但是在NLP任务中,我们引入一个新的思想:在训练外在任务时,再次训练词向量。下面将讨论为什么以及什么时候需要这样做。
3.2 再次训练词向量
正如上面所讨论的,外在任务所使用的词向量,是通过简单的内在任务进行优化的。在很多情况下,这种词向量应用于外在任务都能有良好的表现。词向量可以通过外在任务进一步训练,以便达到更好的效果。不过,再次训练也是有风险的,如果训练语料太少,返回会使情况更糟糕。
3.3 Softmax分类和正则化
让我们分析一下Softmax分类函数的形式:
\begin{align*}
p(y_j=1|x) = \frac{\exp(W_j \cdot x)}{\sum_{c=1}^{C}\exp(W_c \cdot x)}
\end{align*}
上式计算了词向量$x$是类别$j$的概率。使用交叉熵损失函数,对一个训练样本计算如下的损失:
\begin{align*}
-\sum_{j=1}^C y_j \log(p(y_j=1|x)) = -\sum_{j=1}^C y_j \log(\frac{\exp(W_j \cdot x)}{\sum_{c=1}^{C}\exp(W_c \cdot x)})
\end{align*}
事实上,上面的求和,$(C-1)$个都是0,只有$y_j$是1。假设$k$是正确类别的索引,上式可以简化为:
\begin{align*}
-\log(\frac{\exp(W_k \cdot x)}{\sum_{c=1}^{C}\exp(W_c \cdot x)})
\end{align*}
将上面的损失函数扩展到训练集的$N$个点:
\begin{align*}
-\sum_{i=1}^{N} \log(\frac{\exp(W_{k(i)} \cdot x^{(i)})}{\sum_{c=1}^{C}\exp(W_c \cdot x^{(i)})})
\end{align*}
其中,$k(i)$是一个函数,返回实例$x^{(i)}$所对应的正确类别的索引。
让我们来估计一下,如果同时训练模型权重$W$和词向量$x$,需要更新的参数个数。对于一个简单的线性决策边界,模型至少需要一个$d$维的输入词向量,并且产生$C$个类别的分布。因此,更新模型参数至少是更新$C \cdot d$个参数。如果同时更新词库$V$中的每一个词,那就需要更新$\left | V \right |$个词向量,这是$\left | V \right | \cdot d$个参数。所以总共需要更新的参数个数是$C \cdot d + \left | V \right | \cdot d$。这是数量是巨大的,很容易造成过拟合。解决方案也很简单,增加正则项:
\begin{align*}
-\sum_{i=1}^{N} \log(\frac{\exp(W_{k(i)} \cdot x^{(i)})}{\sum_{c=1}^{C}\exp(W_c \cdot x^{(i)})})
+ \lambda \sum_{k=1}^{C \cdot d + \left | V \right | \cdot d} \theta_k^2
\end{align*}
本文翻译自CS224n课程的官方笔记2,对应该课程的第3、4节。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号