ansj构造最短路径

一、前言

上节介绍了ansj的原子切分和全切分。切分完成之后，就要构建最短路径，得到分词结果。

以“商品和服务”为例，调用ansj的标准分词：

?

1 2 3

String str = "商品和服务" ; Result result = ToAnalysis.parse(str); System.out.println(result.getTerms());

先不管数字发现、人名识别、用户自定义词典的识别，暂时只考虑ToAnalysis类里面，构建最短路径的这行代码：

?

1	graph.walkPath();

上面这行代码执行前，已完成了全切分，构建了如下的有向无环图：

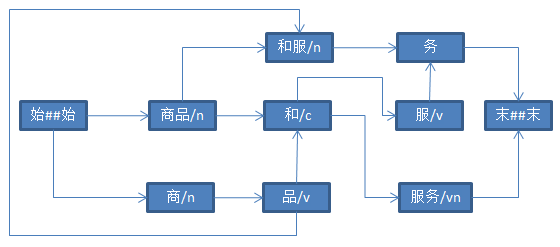
事实上，此时没有“务”这个节点

如上图所示，terms[4] = null。

不过这也没关系，后面给节点打分时，会填充这个null，这段代码位于Graph.merger(Term fromTerm, int to, Map<String, Double> relationMap)：

?

1 2 3 4 5 6

char c = chars[to]; TermNatures tn = DATDictionary.getItem(c).termNatures; if (tn == null || tn == TermNatures.NULL) { tn = TermNatures.NULL; } terms[to] = new Term(String.valueOf(c), to, tn);

也就是说，给“和服”的后继节点打分时，发现其后继节点为null，那么就实例化一个Term，填充在terms[to]的位置。

二、理论基础

两个节点之间分之计算的代码位于MathUtil.compuScore(Term from, Term to, Map<String, Double> relationMap)

其中核心代码只有一行：

?

1	double value = -Math.log(dSmoothingPara * frequency / (MAX_FREQUENCE + 80000) + (1 - dSmoothingPara) * ((1 - dTemp) * nTwoWordsFreq / frequency + dTemp));

我们了探讨一下这行代码的理论基础。

首先，ansj使用二元语法模型（Bigram）进行分词。Bigram模型对应于一阶Markov假设，词只与其前面一个词相关，其对应的分词模型：

$arg\,max\prod_{m}^{i=1}P({w}_{i}|{w}_{i-1})\, =\,arg\,min-\sum_{m}^{i=1}logP({w}_{i}|{w}_{i-1})$

该等式将求解最大联合概率的问题转化为了求解有向无环图最短路径问题。

其中，数学符号arg表示使目标函数取最小值时的变量值。这里是指求解条件概率之积$\prod_{m}^{i=1}P({w}_{i}|{w}_{i-1})$取最大值时的分词结果。

对条件概率$P({w}_{i}|{w}_{i-1})$做如下的平滑处理：

$$\begin{aligned} - \log P(w_{i} | w_{i-1}) & \approx - \log \left[ aP(w_{i-1}) + (1-a) P(w_{i}|w_{i-1}) \right] \\ & \approx - \log \left[ a\frac{f(w_i)}{N} + (1-a) \left( \frac{(1-\lambda)f(w_{i-1},w_i)}{f(w_{i-1})} + \lambda \right) \right] \end{aligned}$$

其中，a = 0.1为平滑因子，N = 207997为训练语料中的总次数，$\lambda \,=\,\frac{1}{N}$。

第一个约等式是采用线性插值法（Linear Interpolation）（可参考自然语言处理：盘点一下数据平滑算法）进行平滑处理。

第二个约等式，我还没搞清楚是什么处理。

三、具体打分流程如下

代码位于Graph.walkPath(Map<String, Double> relationMap)。

Ansj采用了类似于Dijkstra的动态规划算法（作者称之为Viterbi算法）来求解最短路径。

如果存在一条从i到j的最短路径(Vi.....Vk,Vj)，Vk是Vj前面的一顶点，那么(Vi...Vk)也必定是从i到k的最短路径。（可参考Dijkstra算法）

1、从起始节点“始##始”开始，对其后继节点打分

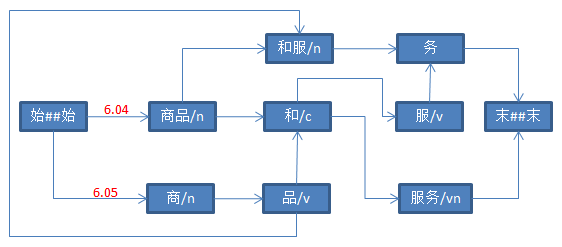
设置“商”、“商品”的前驱节点（也就是Term类的from属性）为“始##始”。

2、计算“商”后继节点的分值

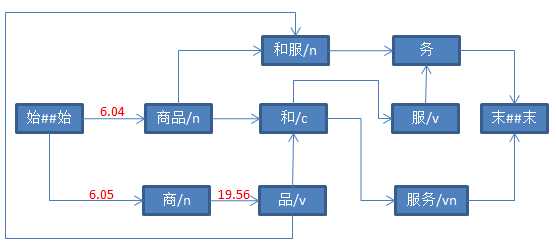
只有一个后继节点“品”。“商”和“品”的分值是13.509，因此从“始##始”到“品”的分值是19.56。

设置“品”的前驱节点为“商”。

3、计算“商品”后继节点分值

设置“和”、“和服”的前驱节点为“商品”。

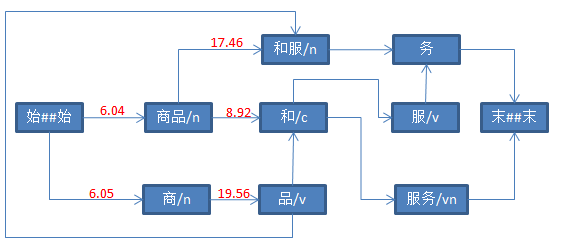
4、计算“品”后继节点分值

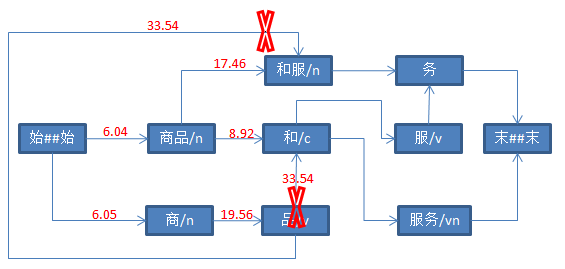
以“和”为例，“和”有“商品”、“品”两个前驱节点。应该取分值最小的那个。因此，“和”的分值依然是8.92，前驱节点依然是“商品”。

同理，“和服”的前驱节点依然是“商品”。

对上图进行简化：

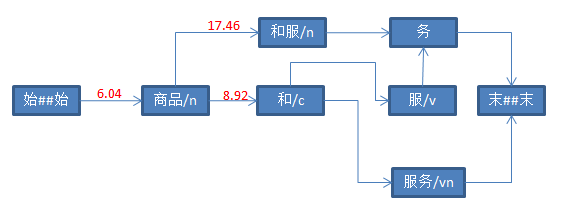
5、计算“和”后继节点分值

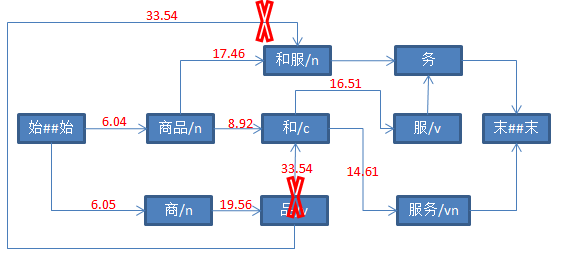
设置“服”、“服务”的前驱节点为“和”。

6、计算“和服”后继节点分值

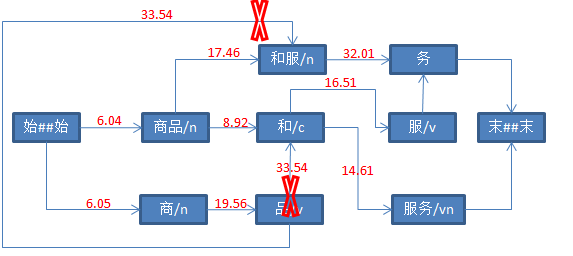
设置“务”的前驱节点为“和服”。

对上图简化：

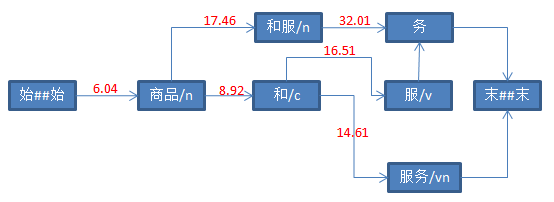
7、计算“服”后继节点分值

“务”以“服”为前驱，可以得到更小的分值。因此，更改“务”的前驱节点为“服”。

对上图简化：

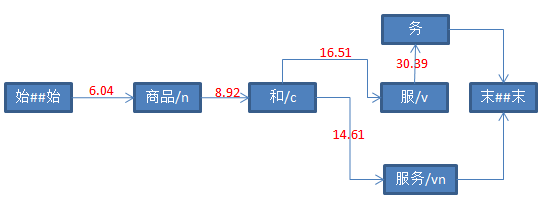
8、计算“服务”后继节点分值

设置“末##末”的前驱节点为“服务”。

9、计算“务”后继节点分值

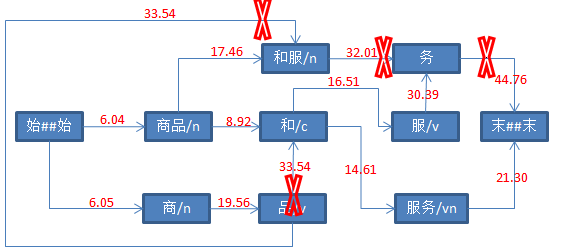
“末##末”以“服务”为前驱节点，分值更新。因此，“末##末”的前驱节点依然是“服务”。

对上图简化：

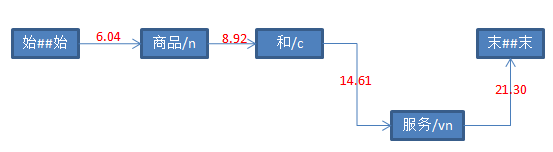
10、设置后继节点

目前已构建了最短路径，并且知道了每个节点的前驱节点。

例如，“末##末”的前驱节点是“服务”。但是并没有将“服务”的后继节点（也就是Term类的to属性）设置为“末##末”。

Graph.optimalRoot()就是设置后继节点的。执行完该方法后，terms被简化为了如下形式：

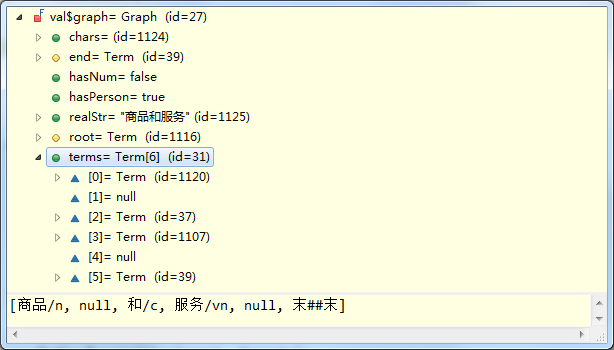
去掉null，就是分词结果了。

参考资料

1、Treant，开源中文分词工具探析（三）：Ansj

2、quicmous，自然语言处理：盘点一下数据平滑算法

3、海 子，Dijkstra算法（单源最短路径）