预测房价的回归问题
回归问题是通过一系列的已知数据预测未来的值,这个待预测的值是一个连续值。我们使用20世纪70年代中期波士顿郊区房价的数据来进行回归问题的讨论。
数据准备
同样的,我们可以使用Keras的内嵌函数加载这批数据,如果网络不支持自动下载,你可以选择事先下载好的数据。
from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) =
boston_housing.load_data(path='/ABS_PATH/boston_housing.npz')
print(train_data.shape, test_data.shape)
print(train_data[0], train_targets[0])
(404, 13) (102, 13)
[ 1.23247 0. 8.14 0. 0.538 6.142 91.7 3.9769 4. 307. 21. 396.9 18.72 ] 15.2
可以看出这组数据有404个训练样本和102个测试样本,每个样本都有13个数值特征,预测的目标是波士顿郊区房屋价格的中位数(单位是千美金)。这些数值特征由于各自的单位不同,取值范围与大小参差不齐,如果直接将这组数据输入到神经网络,势必增加模型学习的困难。所以,我们需要对每个特征进行标准化操作,即对输入数据的每个特征,减去特征的平均值,再除以标准差。
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std
print(train_data[0])
构建网络
我们已经有了电影评论极性分析的实践经验,可以很轻松地堆叠出一个网络模型出来,在这里我们把网络的构建功能封装成了一个函数,为了后面多次使用它。
from keras import models
from keras import layers
def build_model():
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(train_data.shape[1],)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(1))
model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
return model
这个网络模型包含两个中间层,每层都是64个隐藏单元的全连接层,对于第一层需要指定输入数据的维度,我们选择ReLU作为激活函数(你会发现这种带有ReLU激活的Dense层的堆叠,是非常有用的结构,可以解决很多种问题)。这里值得我们注意的是网络的最后一层只有一个单元,没有激活,它是一个线性层,这种设置是标量回归的典型配置。对于回归问题,损失函数通常选择均方误差(MES, mean squared error);训练过程需要监控平均绝对误差(MAE, mean absolute error)。
验证方法
在分析数据时我们已经看到,这批数据的样本量是很少的(只有几百个),如果我们仍然把训练集拆分为训练和验证集,势必导致训练数据不足,同时验证数据太少引发验证得分的波动。所以,在数据样本量较少的情况下,我们建议使用K折交叉验证,这种方法首先将数据集划分为K个分区,实例化K个相同的模型,将每个模型在K-1个分区上训练,并在剩下的一个分区上进行评估,把K次评估得分的平均值作为模型的验证分数。
import numpy as np
k = 4
num_val_samples = len(train_data) // k
num_epochs = 500
all_mae_history = []
for i in range(k):
print('processing fold #', i)
#其中一份作为验证数据
val_data = train_data[i*num_val_samples: (i+1)*num_val_samples]
val_targets = train_targets[i*num_val_samples: (i+1)*num_val_samples]
#剩余各份作为训练数据
partial_train_data = np.concatenate([train_data[:i*num_val_samples],
train_data[(i+1)*num_val_samples:]], axis=0)
partial_train_targets = np.concatenate([train_targets[:i*num_val_samples],
train_targets[(i+1)*num_val_samples:]], axis=0)
model = build_model()
history = model.fit(partial_train_data, partial_train_targets,
validation_data=(val_data, val_targets),
epochs=num_epochs, batch_size=1, verbose=0)
#从hisotry中提取验证结果
mae_history = history.history['val_mean_absolute_error']
all_mae_history.append(mae_history)
当然,除了从history中提取验证结果,也可以手动获取验证得分,此时则不需要在fit函数里指定验证集。
#在验证数据上评估模型
model.fit(partial_train_data, partial_train_targets,
epochs=num_epochs, batch_size=1, verbose=0)
val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
我们计算出每个轮次中所有折MAE的平均值,并使用Matplotlib绘制出指标的变化曲线。
average_mae_history = [np.mean([x[i] for x in all_mae_history]) for i in range(num_epochs)]
import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
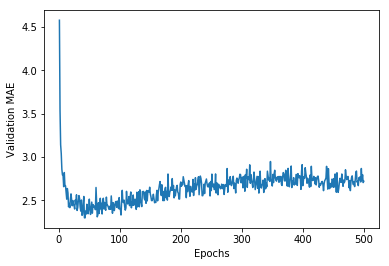
很遗憾,由于数据的方差都相对较大,图片并没有直观地反映出指标的变化趋势。我们需要采取一点小技巧重新绘制:
- 删除前10个数据点,因为它们的取值范围与曲线上的其他点不同
- 将每个数据点替换为前面数据点的指数移动平均值,以得到光滑的曲线
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous*factor+point*(1-factor))
else:
smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:]) #剔除前10个点
plt.plot(range(1, len(smooth_mae_history)+1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
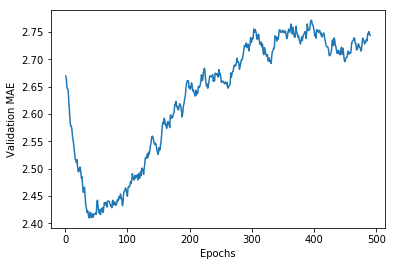
此时的曲线可以很直观地看出,验证MAE在60轮左右就不再显著降低了,此后甚至出现了过拟合。我们用最好的参数(这里只演示了调整轮数)训练最终的生产模型,并观察它在测试集上的性能。
model = build_model()
model.fit(train_data, train_targets, epochs=80, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
print(test_mae_score)
看来,我们预测的房价还是和实际价格相差了约2700美元。
总结
即便本节我们讨论的是回归问题,但是与前一节的电影评论极性分类问题的建模方法论是一样的,针对回归问题,我们可以总结如下:
- 回归问题使用的损失函数通常是均方误差(MSE),评价指标为平均绝对误差(MAE)
- 如果输入的数据的特征具有不同的取值范围,应该先进性预处理,对每个特征单独进行缩放(通常减均值除方差是一种不错的缩放手段)
- 如果数据的验证表现受数据的分布影响,没有明显的趋势可见,可以采取一定的平滑处理以便直观地分析趋势
- 如果可用数据较少,K折交叉验证是首选的验证方法(同样适用于分类问题)



