[C++]线段树 区间修改 单点查询
线段树 区间修改 单点查询
算法思想
由于是区间修改
那就把下放的每一个线段给套上一层标记
来表达增加的值
单点查询就把那些标记穿起来就行了
当然 还要加上那原来的值
来举个例子:
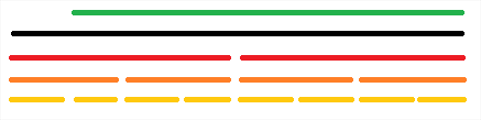
我想要更改绿色这段区间的值
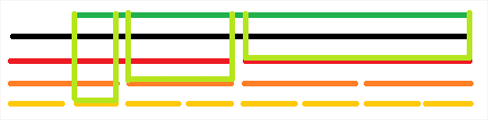
那就在绿色这段上下推标记

然后我又想在蓝色这段上更改区间值
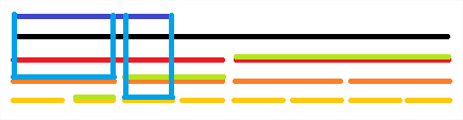
那就继续下推标记

如果我想要查询紫色的这个点的值
那就把一路上的标记(绿色和蓝色的)加起来
最后再把那个点原本的值加起来(黄色那一小段)
就是最终的值了
代码实现
变量含义详见上个Blog
有个新变量就是那个标记
就是 Node 结构体中的 k
Build函数和上个相同
添加标记
void add(int i,int l,int r,int k){
if(l <= tree[i].l && tree[i].r <= r){
tree[i].k += k;
return ;
}
if(tree[li].r >= l)
add(li,l,r,k);
if(tree[ri].l <= r)
add(ri,l,r,k);
}
- \(l <= tree[i].l\) && \(tree[i].r <= r\)
这代表这个线段已经完全被包围了
那就把这个线段打上标记
并且要停止继续向下打标记
因为这段已经打上了
所以 \(return ;\)
- \(tree[li].r >= l\)
- \(tree[ri].l <= r\)
这里和上个相同
哪有搜哪里
单点查询
int search(int i,int dis,int ans){
if(tree[i].l == tree[i].r){
return val[dis] + tree[i].k;
}
if(dis <= tree[li].r)
return tree[i].k + search(li,dis,ans);
if(dis >= tree[ri].l)
return tree[i].k + search(ri,dis,ans);
}
- \(tree[i].l == tree[i].r\)
已经查询到点了
那就返回点的值和这个线段上的标记
- \(dis <= tree[li].r\)
- \(dis >= tree[ri].l\)
如果没有到点
那就加上这个线段的标记
以及继续往下搜的结果
Code
#include<bits/stdc++.h>
#define maxn 1000010
#define mid ((l+r)>>1)
#define li i<<1
#define ri 1+(i<<1)
using namespace std;
int n,val[maxn];
struct Node{
int l,r,sum,k;
}tree[maxn];
void Read(){
cin >> n;
for(int i = 1;i <= n;i++)cin >> val[i];
}
void build(int i,int l,int r){
tree[i].l = l;
tree[i].r = r;
if(l == r){
tree[i].sum = val[l];
return ;
}
build(li,l,mid);
build(ri,mid+1,r);
tree[i].sum = tree[li].sum + tree[ri].sum;
return ;
}
void add(int i,int l,int r,int k){
if(l <= tree[i].l && tree[i].r <= r){
tree[i].k += k;
return ;
}
if(tree[li].r >= l)
add(li,l,r,k);
if(tree[ri].l <= r)
add(ri,l,r,k);
}
int search(int i,int dis,int ans){
if(tree[i].l == tree[i].r){
return val[dis] + tree[i].k;
}
if(dis <= tree[li].r)
return tree[i].k + search(li,dis,ans);
if(dis >= tree[ri].l)
return tree[i].k + search(ri,dis,ans);
}
void interaction(){
while(1){
int tot;
cin >> tot;
if(tot == 1){
int dis;
cin >> dis;
cout << search(1,dis,0) << endl;
} else if(tot == 2){
int l,r,k;
cin >> l >> r >> k;
add(1,l,r,k);
} else if(tot == 3){
return ;
}
}
}
int main(){
cout << "query point" << endl << "change section" << endl;
Read();
build(1,1,n);
cout << "query 1" << endl << "change 2" << endl << "break 3" << endl;
interaction();
return 0;
}

