[C++]二叉链-二叉树存储
二叉链存二叉树
预备知识
感谢:
代码参考:CSDN博主「云雨澄枫」的原创文章
代码解析
结构体 BiNode
template<class T>
struct BiNode{
T data;
BiNode<T> *lchild,*rchild;
};
Node 结点
这个结构体就是用来存储二叉链的每一个节点的
- data
表示这个节点所存的值
- *lchild & *rchild
表示指向 左子树 和 右子树 的指针
这样的结构能很好地存下二叉树:
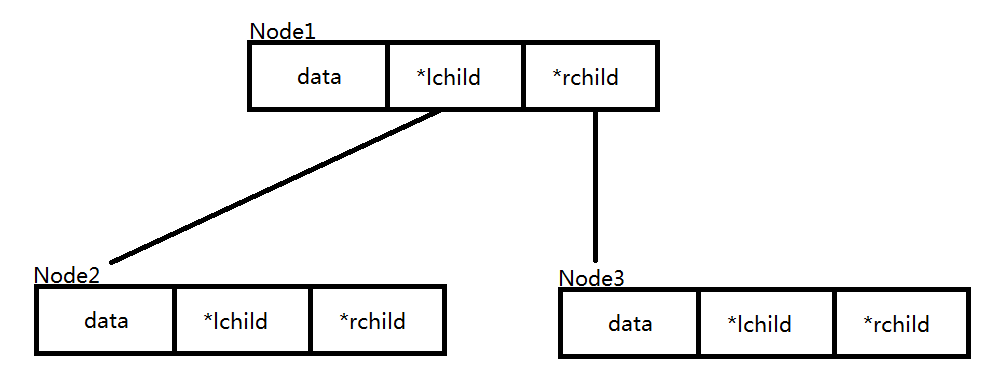
(具体的建树方法会放在后面解释)
类 BiTree
template <class T>
class BiTree{
public:
//构造 & 折构
BiTree(){root = Creat(root);}
~BiTree(){Release(root);}
//遍历
void PreOrder(){PreOrder(root);}
void InOrder(){InOrder(root);}
void PostOrder(){PostOrder(root);}
void LeverOrder();
//树的深度
int Depth(){Depth(root);}
//叶子结点数量
void CaculateLeafNum(){CaculateLeafNum(root);}
//交换左右子树
void swap(){swap(root);}
private:
BiNode<T> *root;//<-根节点在这里
BiNode<T> *Creat(BiNode<T> *bt);
void Release(BiNode<T> *bt);
void PreOrder(BiNode<T> *bt);
void InOrder(BiNode<T> *bt);
void PostOrder(BiNode<T> *bt);
int Depth(BiNode<T> *root);
void CaculateLeafNum(BiNode<T>* root);
void swap(BiNode<T> *root);
};
这便是树的主体
一个 BiTree 的类就代表一颗二叉树
- public
在这里定义了一些之后会用到的函数以及构造函数和折构函数
这里知道有这些东西即可
- private
这里则有一些 public 会用到的函数
以及这个树的根节点
构造函数 & 折构函数
- 构造函数
在类中 是这样写的:
BiTree(){root = Creat(root);}
构造这个树是通过 Creat 这个函数来实现的
Creat_Code:
template <class T>
BiNode<T> *BiTree<T>::Creat(BiNode<T> *bt)
{
T t;
cin >> t;
if(t == '#')
bt = NULL;
else {
bt = new BiNode<T>;
bt->data = t;
bt->lchild = Creat(bt->lchild);
bt->rchild = Creat(bt->rchild);
}
return bt;
}
在讲构造函数之前
还需要提一嘴其输入方式
这里是采用前序遍历的方式进行输入
同时还需要以 "#" 输入叶子结点的空子结点
例子:
cin:
ABD#G###CE##F##
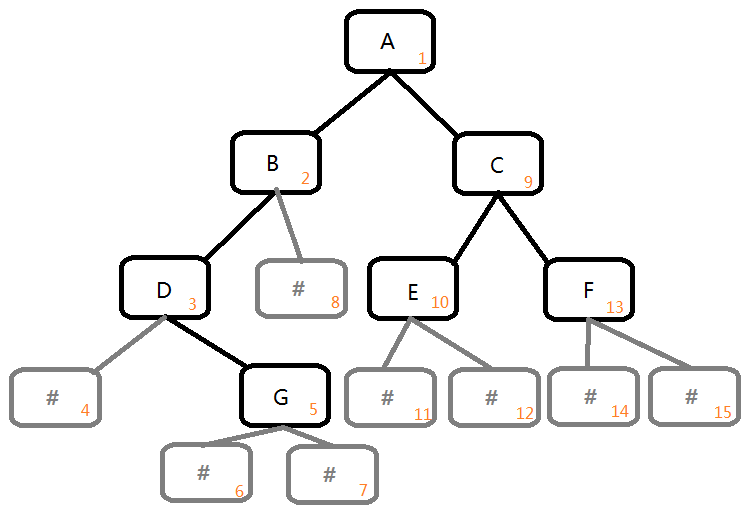
- 图中的序号即代表 cin 中的第几个字符
知道了输入的顺序之后
代码就变得好理解很多了
创建一个结点的时候
首先输入这个结点的值(就是 t)
若其值是 "#" 那就不继续往下面创造新结点了
直接让 bt 为 空指针
并把这个指针返回
若其值不为 "#"
那说明后面可能还有结点需要添加
就继续在左右子结点上调用 Creat函数
bt = new BiNode<T>;
这行代码可能还需要解释一下
new 是用来开辟新的内存空间的关键字
这里相当于开辟了一个新的结点结构体
而 bt 存下了这个结点结构体的指针
- 折构函数
~BiTree(){Release(root);}
折构函数和构造函数一样是用类名来作为函数名的
不过需要在前面加一个 "~"
这个函数调用了 Release 这个函数
template<class T>
void BiTree<T>::Release(BiNode<T> *bt){
if(bt != NULL){
Release(bt->lchild);
Release(bt->rchild);
delete bt;
}
}
delete 用于删除内存的关键词
这个函数因该很好理解
就是从上往下搜
从下往上删
就不过多解释了
遍历函数
这个分两部分将
第一部分 : 前/中/后序遍历
这些代码原理相同 就随便挑一个讲好了
template <class T>
void BiTree<T>::PreOrder(BiNode<T> *bt){
if (bt == NULL)
return;
else {
cout << bt->data;
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
从 root结点 开始搜索
如果不是空结点 那就直接输出
然后往两边找
决定前中后的只在于
输出与往两侧搜索语句的顺序
第二部分 : 层序遍历
还是用这个图
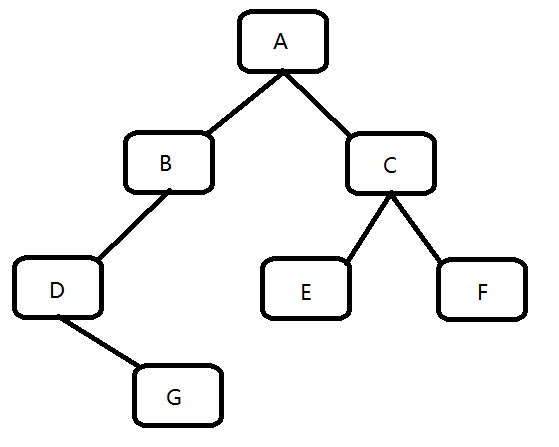
Code:
template<class T>
void BiTree<T>::LeverOrder(){
int front = -1,rear = -1;
BiNode<T> *Q[100];
if(root == NULL) return;
Q[++rear] = root;
while(front != rear){
BiNode<T> *q = Q[++front];
cout << q->data;
if(q->lchild != NULL) Q[++rear] = q->lchild;
if(q->rchild != NULL) Q[++rear] = q->rchild;
}
}
这里是用一个数组和两个变量来实现了队列的功能
接下来我们来模拟一下
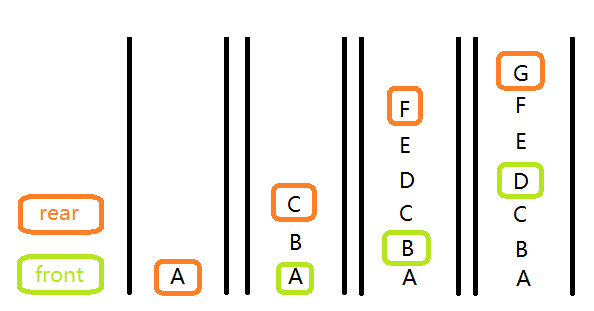
这样就可以实现层序遍历了
求树的深度
Code:
template<class T>
int BiTree<T>::Depth(BiNode<T> *root){
int hl,hr;
if(root == NULL)
return 0;
else{
hl = Depth(root->lchild);
hr = Depth(root->rchild);
return max(hl,hr) + 1;
}
}
深度要找的是最深的叶子结点的层数
因此直接左右找取最大值即可
求叶子结点数量
Code:
template<class T>
void BiTree<T>::CaculateLeafNum(BiNode<T> *root){
if(!root) return;
if(root->lchild == NULL && root->rchild == NULL) Leaf_Count++;
CaculateLeafNum(root->lchild);
CaculateLeafNum(root->rchild);
}
首先我们要知道叶子结点的特征:
没有儿子节点
(就是所有儿子节点都为 NULL)
所以左右搜找到无儿子 +1 即可
交换左右子树
template<class T>
void BiTree<T>::swap(BiNode<T> *root){
BiNode<T> *temp;
if(root == NULL)
return;
else{
temp = root->lchild;
root->lchild = root->rchild;
root->rchild = temp;
swap(root->lchild);
swap(root->rchild);
}
}
由于二叉链的本质就是指针的堆叠
因此直接交换指针的存值就可以了
Code
#include<bits/stdc++.h>
using namespace std;
template<class T>
struct BiNode{
T data;
BiNode<T> *lchild,*rchild;
};
template <class T>
class BiTree{
public:
//构造 & 折构
BiTree(){root = Creat(root);}
~BiTree(){Release(root);}
//遍历
void PreOrder(){PreOrder(root);}
void InOrder(){InOrder(root);}
void PostOrder(){PostOrder(root);}
void LeverOrder();
//树的深度
int Depth(){Depth(root);}
//叶子结点数量
void CaculateLeafNum(){CaculateLeafNum(root);}
//交换左右子树
void swap(){swap(root);}
private:
BiNode<T> *root;
BiNode<T> *Creat(BiNode<T> *bt);
void Release(BiNode<T> *bt);
void PreOrder(BiNode<T> *bt);
void InOrder(BiNode<T> *bt);
void PostOrder(BiNode<T> *bt);
int Depth(BiNode<T> *root);
void CaculateLeafNum(BiNode<T>* root);
void swap(BiNode<T> *root);
};
int Leaf_Count = 0;
template <class T>
BiNode<T> *BiTree<T>::Creat(BiNode<T> *bt)
{
T t;
cin >> t;
if(t == '#')
bt = NULL;
else {
bt = new BiNode<T>;
bt->data = t;
bt->lchild = Creat(bt->lchild);
bt->rchild = Creat(bt->rchild);
}
return bt;
}
template<class T>
void BiTree<T>::Release(BiNode<T> *bt){
if(bt != NULL){
Release(bt->lchild);
Release(bt->rchild);
delete bt;
}
}
template <class T>
void BiTree<T>::PreOrder(BiNode<T> *bt){
if(bt == NULL)
return;
else {
cout << bt->data;
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
template<class T>
void BiTree<T>::InOrder(BiNode<T> *bt){
if(bt == NULL)
return;
else{
InOrder(bt->lchild);
cout << bt->data;
InOrder(bt->rchild);
}
}
template<class T>
void BiTree<T>::PostOrder(BiNode<T> *bt){
if(bt == NULL)
return;
else{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout << bt->data;
}
}
template<class T>
void BiTree<T>::LeverOrder(){
int front = -1,rear = -1;
BiNode<T> *Q[100];
if(root == NULL) return;
Q[++rear] = root;
while(front != rear){
BiNode<T> *q = Q[++front];
cout << q->data;
if(q->lchild != NULL) Q[++rear] = q->lchild;
if(q->rchild != NULL) Q[++rear] = q->rchild;
}
}
template<class T>
int BiTree<T>::Depth(BiNode<T> *root){
int hl,hr;
if(root == NULL)
return 0;
else{
hl = Depth(root->lchild);
hr = Depth(root->rchild);
return max(hl,hr) + 1;
}
}
template<class T>
void BiTree<T>::CaculateLeafNum(BiNode<T> *root){
if(!root) return;
if(root->lchild == NULL && root->rchild == NULL) Leaf_Count++;
CaculateLeafNum(root->lchild);
CaculateLeafNum(root->rchild);
}
template<class T>
void BiTree<T>::swap(BiNode<T> *root){
BiNode<T> *temp;
if(root == NULL)
return;
else{
temp = root->lchild;
root->lchild = root->rchild;
root->rchild = temp;
swap(root->lchild);
swap(root->rchild);
}
}
int main(){
BiTree<char>* bitree=new BiTree<char>;
cout<<"前序遍历";
bitree->PreOrder();
cout << endl;
cout<<"中序遍历";
bitree->InOrder();
cout << endl;
cout<<"后序遍历";
bitree->PostOrder();
cout << endl;
cout<<"层序遍历";
bitree->LeverOrder();
cout << endl;
cout<<"深度:"<<bitree->Depth()<<endl;
bitree->CaculateLeafNum();
cout<<"叶子结点个数:"<<Leaf_Count<<endl;
bitree->swap();
cout<<"左右子树交换后的层序:";
bitree->LeverOrder();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号