1,

2,

3,多元线性回归权值参数W的求解,X为各个变量

4,liner bias
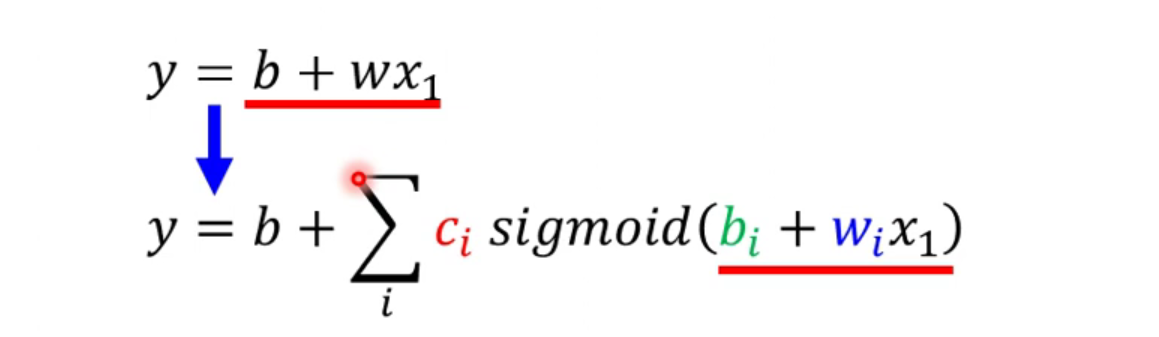
怎么去理解?
线性模型偏差:如果只是一组w和b的话,x和y的关系永远是正比或者是反比,但是现实问题往往是比较复杂的,比如在某个范围内是成正比,但是一旦超过某些范围就成了反比。
比如下面的红线,只有一组位置参数w和b的情况下,无论选择设定值是多少,都无法拟合成红线的样子。这样的限制叫做线性模型的偏差。

那么怎么办?
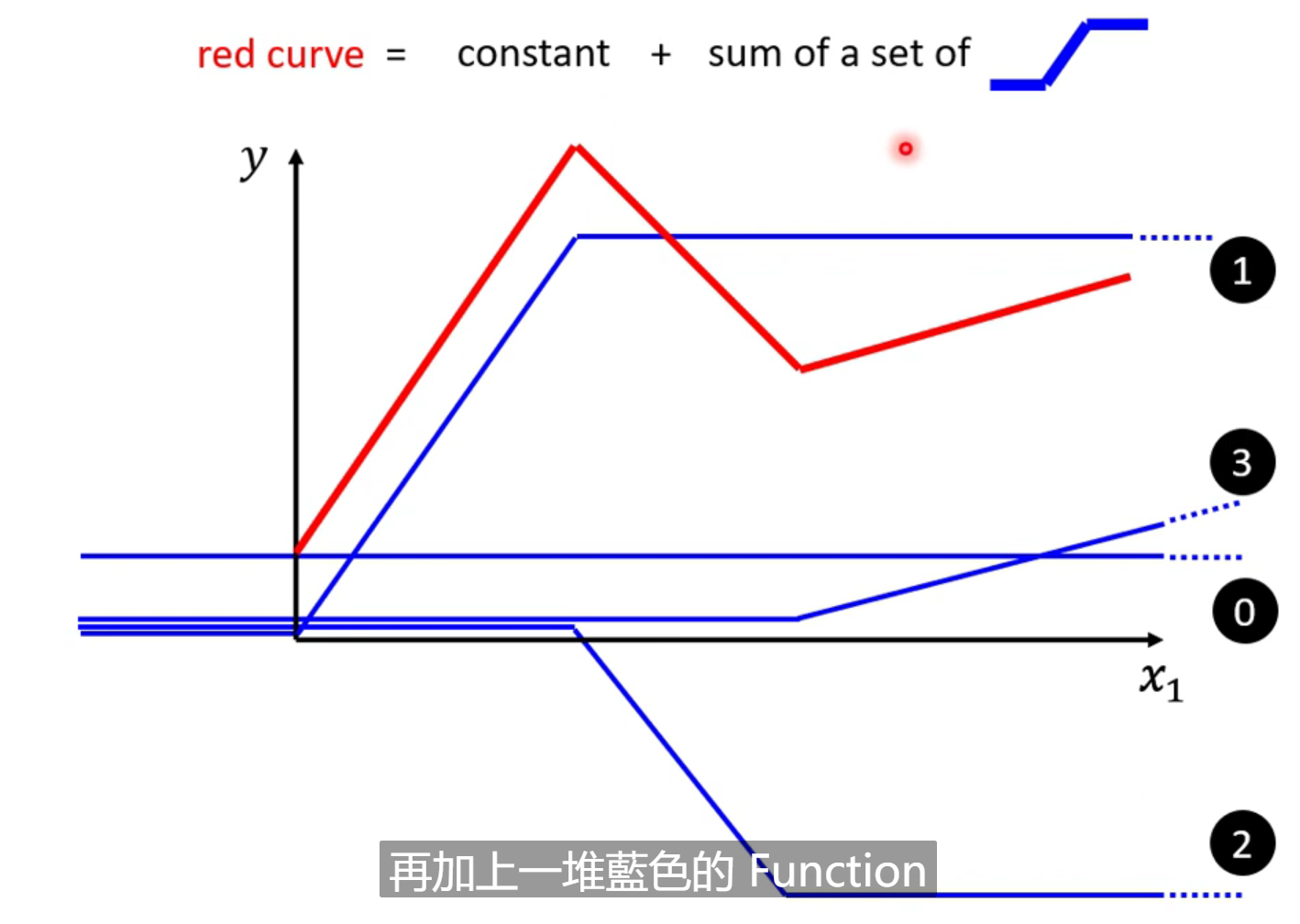
这样看来。任何的分段函数的图形都可以有不同的蓝色函数来和常数相加得到。越复杂的红色线段,也许用到的蓝色方程越多。而只要点取得够多且位置恰当,可以无限逼近我们需要的连续函数。

那么x和y的关系也许非常复杂,但是只要我们设定了一定的蓝色小方程和合适的常数值,就可以去画出我们需要的复杂曲线的近似曲线(用分段函数去逼近)。
而蓝色 方程我们要怎么样表示出来呢?
我们可以看到形状非常像sigmoid函数图像,那么我们就可以用sigmoid去近似替代我们需要的蓝色方程。蓝色方程我们又叫做hard sigmoid(其实直接用hard sigmoid来也可以,虽然表示起来比较难一些,可以用两个reLU去合成hard sigmoid函数,使用reLU往往比下面的liner模型更好。)。

我们通过改变sigmoid方程的三个参数c,b和w,就可以得到不同的soigmoid函数,不同的sigmoid函数叠加起来之后就可以得到不同分段函数,再去近似得到连续函数。
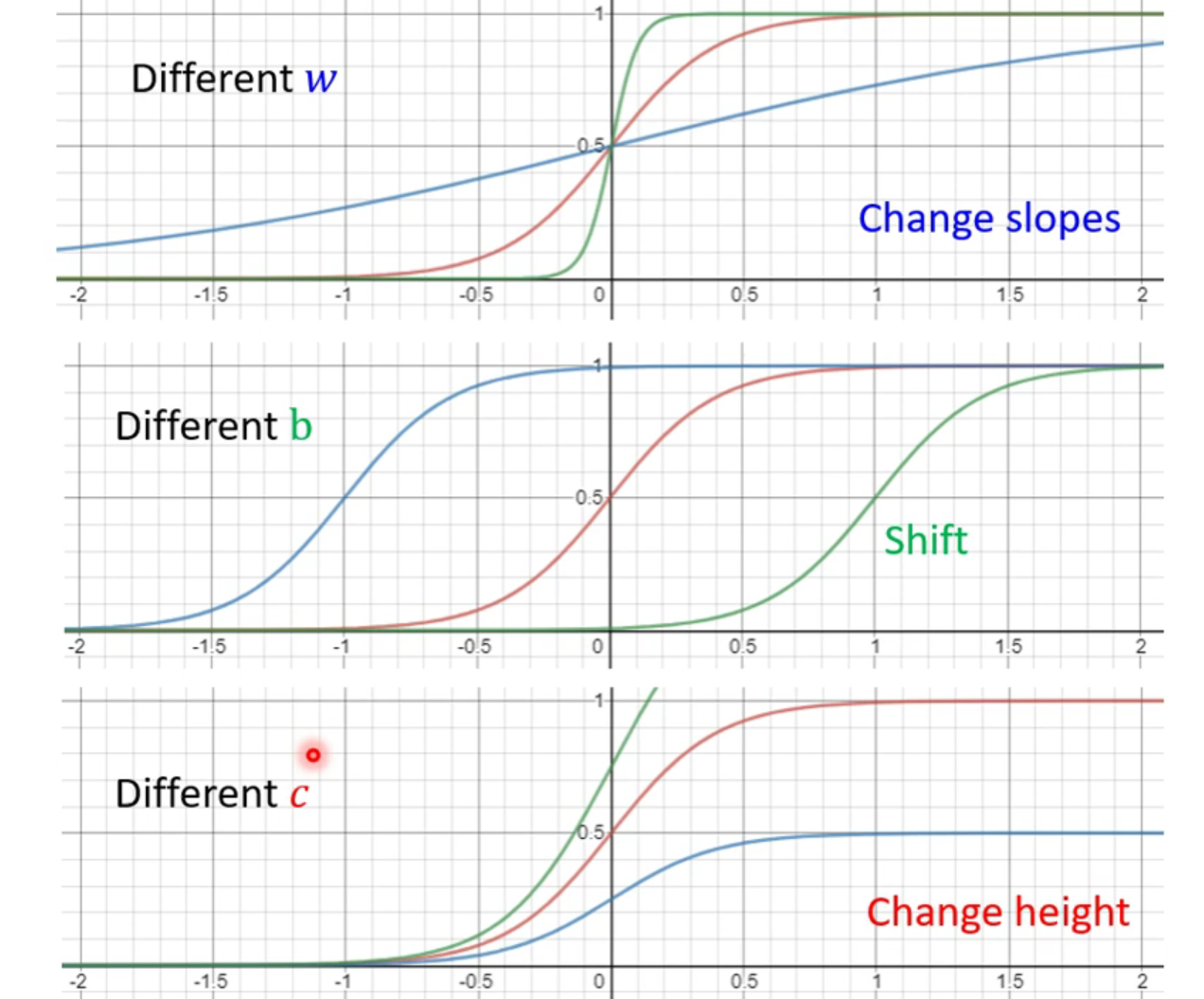

上面是只有一个特征x1,那么考虑多个特征值的时候是什么样的呢?比如YouTube订阅量预测,不仅仅考虑前一天的数据,而是考虑前三天的数据。

假设特征参数有三个,x1x2x3,那么



那么机器学习第一步就完成了,得到一个包含未知参数的方程。就可以依据这个方程得到loss方程。就可以进行后面的步骤。
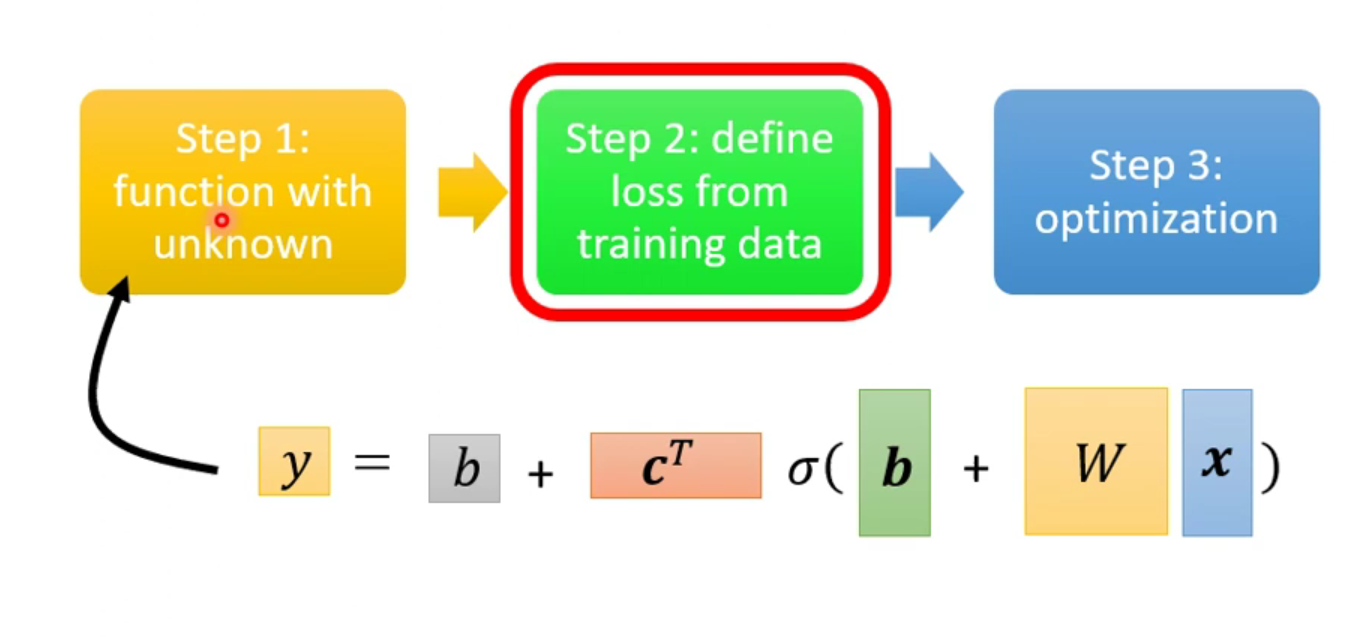
5,优化和泛化
优化(optimization)是指调节模型以在训练数据上得到最佳性能(即机器学习中的学习),而泛化(generalization)是指训练好的模型在前所未见的数据上的性能好坏。机器学习的目的当然是得到良好的泛化,但你无法控制泛化,只能基于训练数据调节模型。
6,过拟合和欠拟合
所谓过拟合,就是指模型在训练集上表现较好,但在验证集或测试集上表现一般,泛化能力弱。打个比方,有个学生,他在学习过程中记住了他做过的所有的题型,但是他就只会做他做过的题,当遇到题目稍微有变化或者新题目,他就无从下手了。这就是典型的“过拟合”,也就是说该学生过度记住之前的题目特征,而没有学习到好的“解题方法”,导致他遇到新题的时候不能做到举一反三。
欠拟合与过拟合是恰好相反的情况,欠拟合是指模型在训练集上表现差,在验证集或测试集上表现也同样较差,模型几乎没有泛化效果。我们还是以学生的学习能力为例,假设现在有个学生,上课他总是睡觉,不听课课后也不自学,导致他考试时不管是做过的还是没做过的题他都不会做,考试总是垫底,这就是典型的欠拟合。
它不仅在训练数据(旧的)集上有较好的表现,且对新的数据样本也有同样具有优异的泛化能力。


