一，无符号数&有符号数
1）无符号数
2）上图如果是16位寄存器，有符号数可以表示-32768~32787
二，真值和机器数
带符号“+”“-”的数称为真值，把符号数字化的数称为机器数。如下面例子（纯整数或纯小数，区分开浮点数，比如+123.123）：
机器数又有不同的表示方式，其中原码是最简单直接的一种。
1）原码：用一位符号位表示正负，数值位表示对应真值的绝对值。
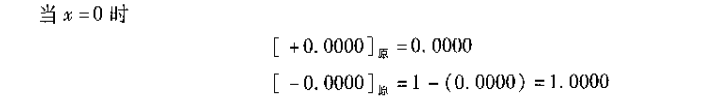
2）补码： 解决了原码运算归一化的问题。
以时钟为例子，12为模，想要6点变为3点，那么一种方法是减3，另外一种方法是加上以模12为基准3的补数，也就是加上9，再减去模本身。可以看到减去一个数，可以用加上它的补数来替代。减法就变成了加法。
来到机器码，
上面例子+0101是-1011的补码。
那么一个数的补码怎么求：正数的补码等于它的原码；负数的补码等于”它的符号位不变，其余位取反“也就是反码，再加1。
综上，补码最大的好处是可以将减法转化为加法。
3）移码
如果采用移码，也就是真值x加上2的n+1次方。就可以很方便的判断大小了。
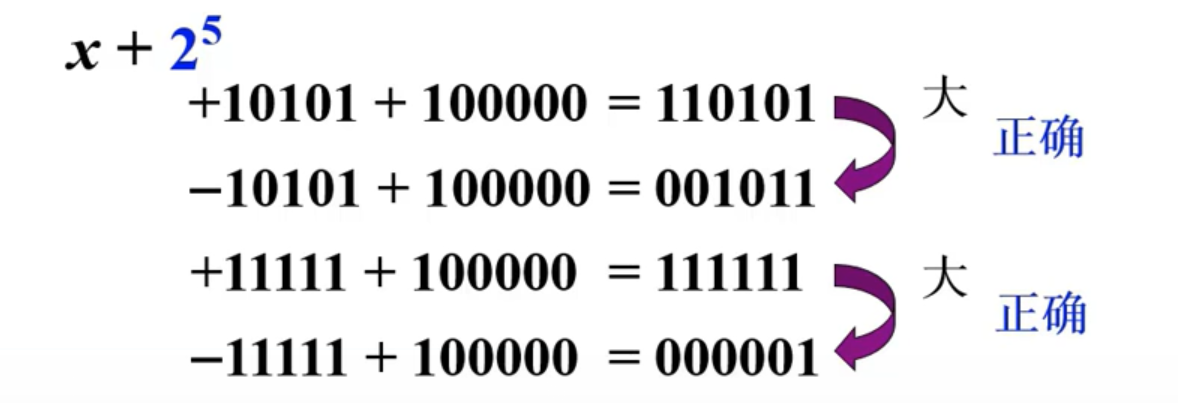
三，数的定点和浮点表示
1）定点表示：小数点以约定方式标出。计算机中没有专门的硬件来表示小数点，是计算机体系架构设计人员约定的。在硬件实现和软件设计中都要遵循这一约定。
定点有以下两种：
上图左边例子表示存放的定点数都是小数，而右边表示存放的都是整数。这是约定好的。
2）浮点表示：早期的计算机只有定点运算方式，也就是小数定点机或者整数定点机，但是我们科学运算常常要使用浮点数来进行运算。所以早期会造成编程十分困难，程序员要调整小数点的位置。再者，定点数能表示的数的范围很小，如果要表示相差的大的数，需要很长的机器字长，同时造成存储空间的利用率很低。
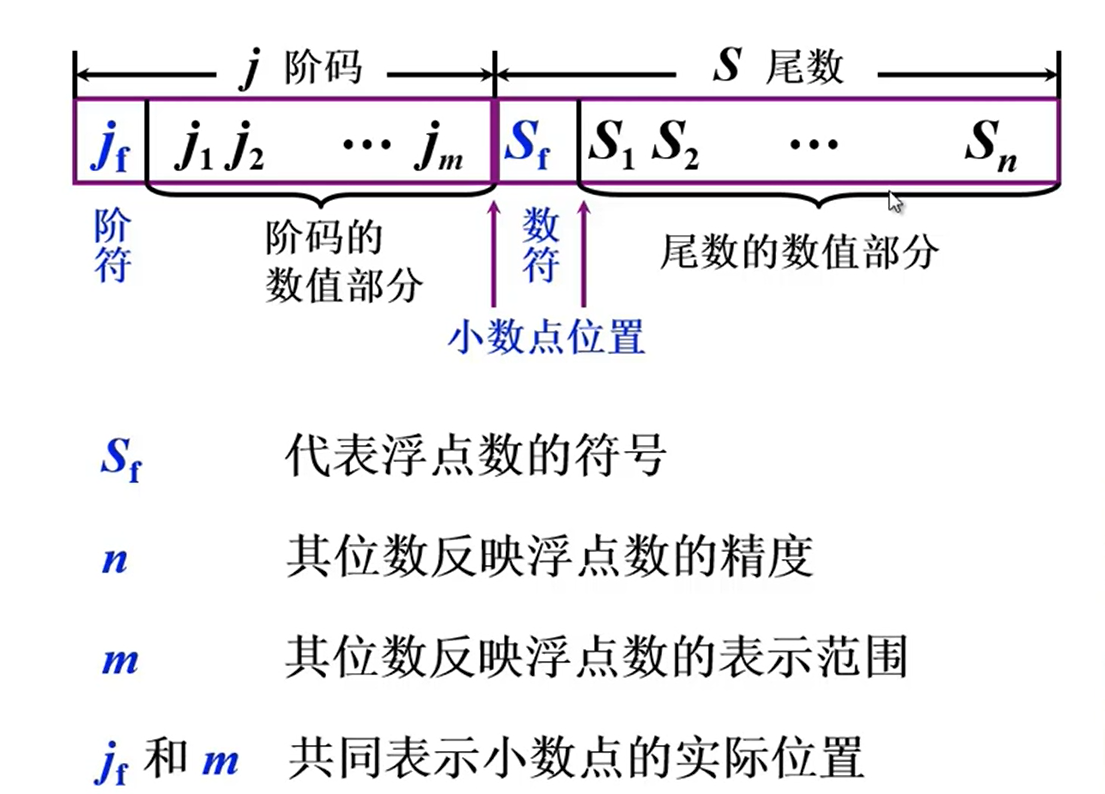
浮点数的规格化：
