《鱿鱼游戏》中【过玻璃桥】游戏的概率问题

 

这周在B站上看MIT的CS6.0001（作为一条计算机基础菜狗，上这课真是大补。老师讲的真得超好，强烈安利第六讲，第十讲到第十二讲）。

今天还剩最后一讲，狠狠奖励自己（快乐地摸了摸鱼），点开了《鱿鱼游戏》，开始回味第七集【过垫脚石桥】。

 

为了方便没有看过该剧的读者理解，在这里描述下游戏规则：

 

有16位选手要过一条玻璃桥。

玻璃桥由18组玻璃构成。每组玻璃由两块玻璃平行组成，1块是钢化玻璃，1块是普通玻璃。

钢化玻璃能承重，如果选手踩到钢化玻璃可以继续前行；但如果踩到普通玻璃，玻璃会碎掉，选手死亡。

选手按号码依次前行，通过18组玻璃后算作存活。

 

玻璃桥直观图片：

 选手们如何过桥（放张没那么血腥的）：

 

比较有意思的是，剧里面的3号选手（是一个数学老师）发现前面还有15组玻璃时，绝望地说过桥的概率只有1/(2^15)，因此不顾一切地飞奔（按照概率预想的gg了）。

 

由此我想到了一些相关问题：

【问题1】16位选手，在排除其他因素的情况下，期望能够有多少人可以存活？

【问题2】每个人的期望生存概率是多少咧？

【问题3】直观上感觉16号成奇勋（主角）肯定能活，是对的吗？

 

作为一条菜狗，我当然没有想到蒙特卡洛解法（为什么这么理直气壮），老师说先从小问题算起，那就来个最基础的problem吧。

 

垫脚石桥嘛，前面一个人帮后面的人探路。

最好情况，1号win the lottery，战胜了1/（2^18）概率，带领16个人全通关了。

最坏情况，前面的人都是倒霉蛋，全踩到普通玻璃做了垫脚石，因此16号奇勋同志前面还有3组玻璃，那么他有1/（2^3）【12.5%】的概率可以存活（运气背起来也太背了……）。

 

下面考虑一种直观情况。假设每个玩家都能通过一组玻璃，然后在第二组玻璃的时候领便当。

这种情况下每个人踩了别人之后，生存的概率是均等的，近似于生存的平均情况。

 

上个图【取了剧中的配色，对比色能搭成这样真得很好看！深粉色：#E54D91；深绿色：#004A46；浅粉色（excel自带）：#FFCCFF】

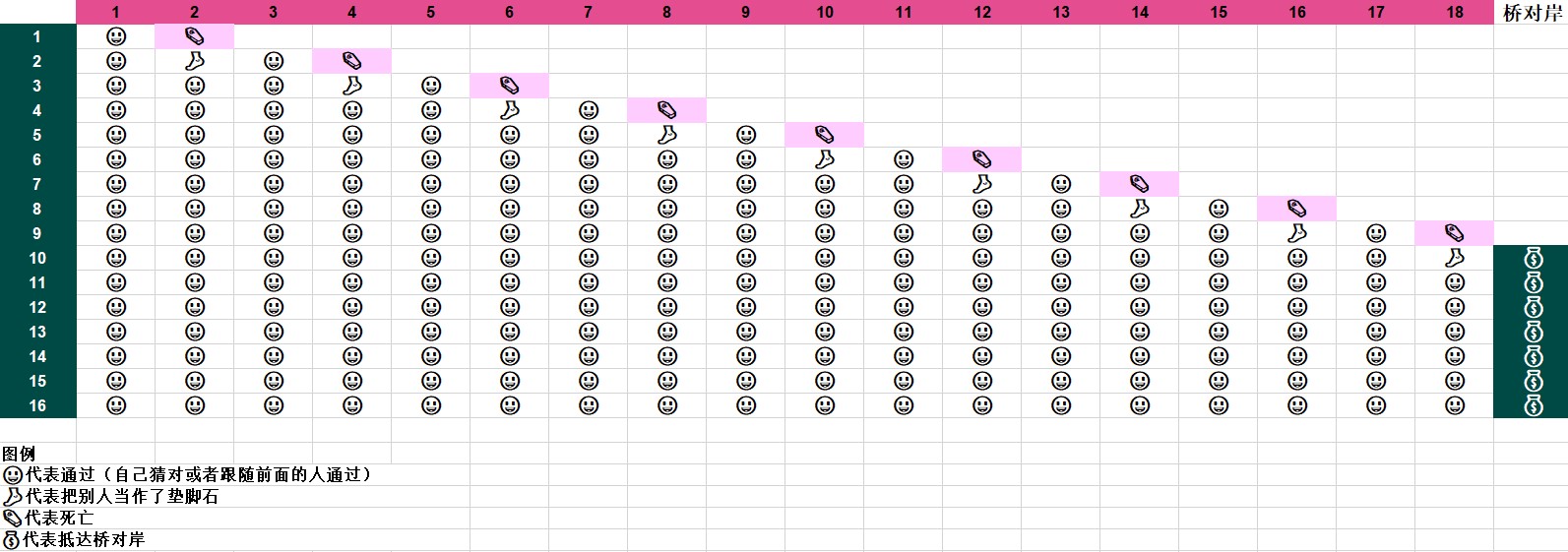
在这种情况下，有7个人可以到达桥对岸。

但我咋证明它确实是平均情况咧？？？？

 

面向搜索引擎编程，启动！

 

计算思维的本质是自动化+抽象。

看到概率问题，为什么不用蒙特卡洛算法呢？

看到概率问题，为什么不用蒙特卡洛算法呢？

看到概率问题，为什么不用蒙特卡洛算法呢？

模拟下真实情况就好了呀！！！（下面为大家播送大佬们的两个帖子，写得很详细清晰）

 

计算最有可能通过的人数（java）：https://www.cnblogs.com/bryan31/p/15420470.html

大佬模拟了1亿次，得出存活7人的可能性最高。

 

计算每个人的生存概率（python）：https://www.cnblogs.com/dingdangsunny/p/15435513.html

大佬模拟了100万次，得到如下结论（图源自上述地址）：

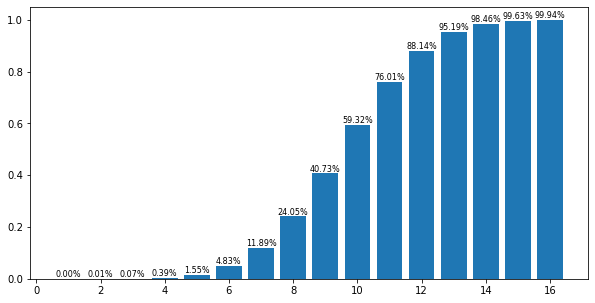
 一般而言，16号奇勋同志真是稳赢啊！

 

所以今天真的有狠狠get到计算思维的魅力哈哈。

那么这个问题就这样收尾啦（好草率的收尾），感觉这个问题很适合作为教学案例呢。

E54D91