Canny算法简解

Canny理论：

1、首先用高斯模糊过滤掉噪声

2、然后用 Sobel 过滤器确定图像边缘的强度和方向

Gx是指梯度在x方向上的突变，也就是垂直边缘

Gy是指梯度在y方向上的突变，也就是水平边缘

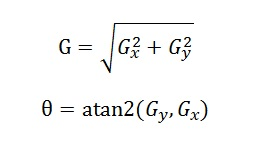
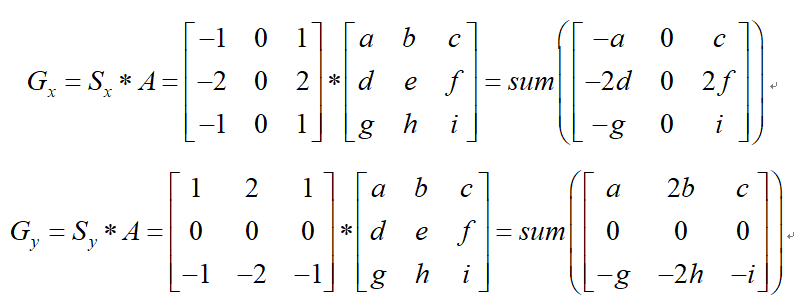
根据以上公式可以求出梯度及方向。

3、对sobel的输出使用非极大抑制来观察每个检测边缘的强度和方向，选出局部最大像素，从而把最强的边缘绘制成连续的、一个像素宽的细线。Canny算子中的非极大值抑制是沿着梯度方向进行的，即是否为梯度方向上的极值点；而在角点检测等场景下说的非极大值抑制，则是检测中心点处的值是否是某一个邻域内的最大值，是，则保留，否则去除，这种情况下的非极大值抑制比较简单。

(a.) canny算子中非最大抑制(Non-maximum suppression)是回答这样一个问题: “当前的梯度值在梯度方向上是一个局部最大值吗?” 所以,要把当前位置的梯度值与梯度方向上两侧的梯度值进行比较. 
(b.) 梯度方向垂直于边缘方向, 这一点不要误解.

要进行非极大值抑制，就首先要确定像素点C的灰度值在其8值邻域内是否为最大。图1中蓝色的线条方向为C点的梯度方向，这样就可以确定其局部的最大值肯定分布在这条线上，也即出了C点外，梯度方向的交点dTmp1和dTmp2这两个点的值也可能会是局部最大值。因此，判断C点灰度与这两个点灰度大小即可判断C点是否为其邻域内的局部最大灰度点。如果经过判断，C点灰度值小于这两个点中的任一个，那就说明C点不是局部极大值，那么则可以排除C点为边缘。这就是非极大值抑制的工作原理。

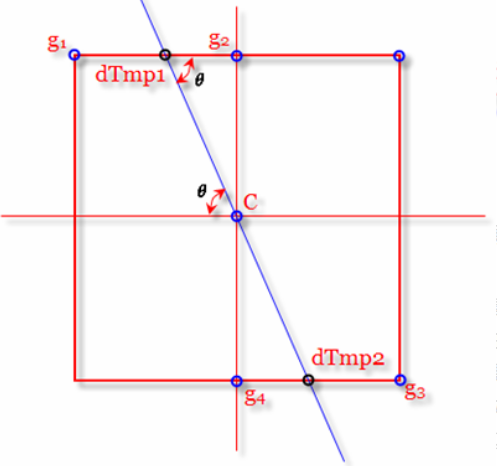
因为算完梯度后边缘很粗，作者论文中假设边缘都是单个像素，因此在每个边缘的垂直方向（即梯度方向）保留最大值。

要得到dTmp1和dTmp2就需要对该两个点两端的已知灰度进行线性插值，也即根据图1中的g1和g2对dTmp1进行插值，根据g3和g4对dTmp2进行插值，这要用到其梯度方向，这是上文Canny算法中要求解梯度方向矩阵Thita的原因。

 

4、最后 用滞后阀值来分离最佳边缘。滞后阀值是双阀值化操作，以某图一像素宽的横切面为例，这里的曲线代表边缘强度，峰值指的是十分强的边缘。使用滞后阀值时 我们要确定一个高阀值 以便允许这些强边缘通过，再设置一个低阀值，任何低于该阀值的边缘即为弱边缘 会被舍弃。但位于高低阀值之间的边缘只有当其与另一个强边缘相连时 才会得到保留。这样Canny 就删除了弱边缘、消除了噪声，还将关联最强的那些边缘分离了出来，而这些边缘恰恰最可能是物体边界的一部分。高阈值和低阈值的比率应为2：1，3:1 。

 

 

 

代码实现：

import numpy as np
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
image = cv2.imread('3.png')
image_copy = np.copy(image)
image_copy = cv2.cvtColor(image_copy,cv2.COLOR_BGR2RGB)
plt.imshow(image_copy)

gray = cv2.cvtColor(image_copy,cv2.COLOR_RGB2GRAY)
plt.imshow(gray,cmap='gray')

lower =120
upper =240
edge = cv2.Canny(gray,lower,upper)
plt.imshow(edge,cmap='gray')

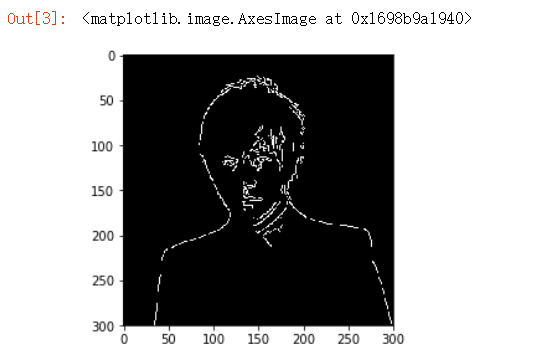
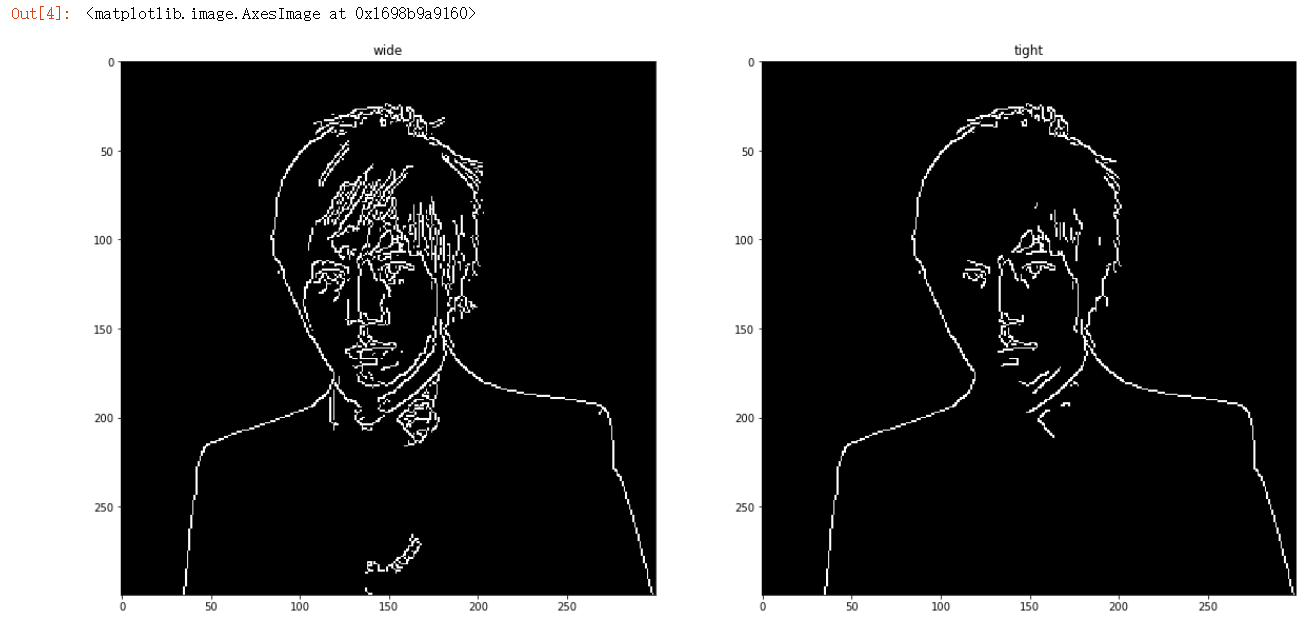
wide = cv2.Canny(gray,30,100)
tight = cv2.Canny(gray,180,240)
f,(ax1,ax2) = plt.subplots(1,2,figsize=(20,10))
ax1.set_title('wide')
ax1.imshow(wide,cmap='gray')
ax2.set_title('tight')
ax2.imshow(tight,cmap='gray')