前缀和和差分

前缀和

定义前缀和 S(i)= a1 + a2 + a3 + ... + ai，且S0 = 0

作用：对于一个区间[l, r]求和，可直接用S(r) - S(i-1)求得

对于二维，某一区域的数组之和，同样可使用前缀和思想

 

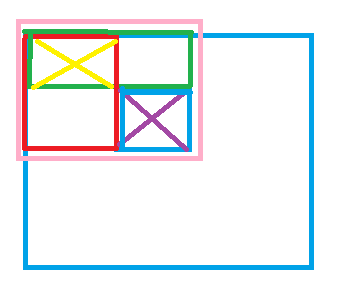
用S(i, j)表示前i行，j列元素之和，若求紫色区域面积，只需要用S(粉) - S(红) - S(绿) + S(黄)

S(i, j) = S(i-1, j) + S(i, j-1) - S(i-1, j-1) + a(i, j)

紫色边界为x1, y1, x2, y2，紫色面积为S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1]

差分

已知a1, a2, a3, ..., an

构造b1, b2, b3, ..., bn

使用ai = b1 + b2 + ... + bi

作用：若要对a在某一区间的元素均加上一个常数，并多次进行这样的操作，可用差分节约时间

若对ai在[l, r]区间上的元素加上一个常数c，只需要将b[l]加上c，b[r+1]减去c,然后对于b[i]积分即可

若进行多次这样的操作，只需要在每一次操作时将b[l]加上c，b[r+1]减去c， 最后对b[i]只需一次积分

trick: 差分数组的构建

将a1, a2, a3, ...,an数组看作是由0， 0， 0，  ... ，0分别在[i, i](i取1, 2, 3, ..., n)加上常数a1, a2, a3, ..., an而来

原理：

当a1, a2, a3, ...,an数组为0， 0， 0，  ... ，0， 差分数组b1, b2, b3, ..., bn为0， 0， 0，  ... ，0，

当0， 0， 0，  ... ，0数组分别在i(i取1, 2, 3, ..., n)加上常数ai时

我们需要一个操作来保证，除位置i元素变为ai，其余元素不变

并且每一次操作后，b1, b2, b3, ...,bn仍是an的前缀和

即在每一次操作时将b[l]加上a[i]，b[i+1]减去a[i]

这种操作并没有改变b1, b2, b3, ...,bi-1的值，并且b1, b2, b3, ...,bi-1, bi满足前缀和等于ai

 

 

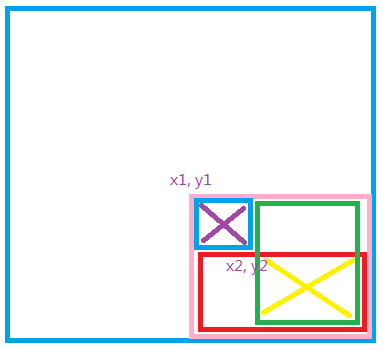
对于二维，对多区域的分别加上不同常数，同样可使用差分思想

若对紫色区域每一个元素均加常数c，则等价于b(x1, y1) += c, b(x2+1, y1) -= c, b(x1, y2+1) -=c, b(x2+1, y2+1) +=c

若x1 = x2 = i, y1 = y2 = j，则b(i, j) += c, b(i+1, j) -= c, b(i, j+1) -=c, b(i+1, j+1) +=c

最后对于b[i][j]积分即可