对称加密和公钥加密
目录
对称加密和公钥加密
加密用于保证机密性。本文总结对称加密和公钥加密的优缺点及两者比较。主要材料来自于Handbook of Applied Cryptography一书。
加密方案的安全性
必要不充分条件: 密钥空间大到排除穷搜
对称密码学
采用对称密钥加密的双方通信可用下图表示，对称密码的一个主要问题是寻求有效的方法进行密钥协商及交换。
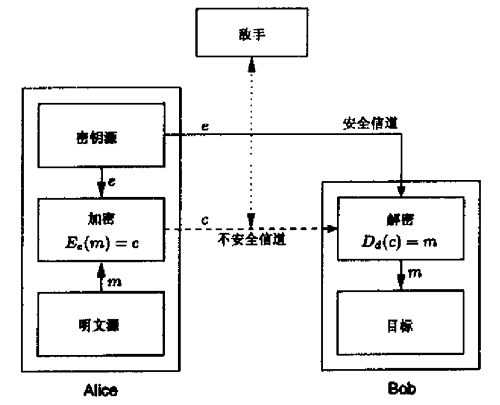
对称密钥加密的密钥管理问题
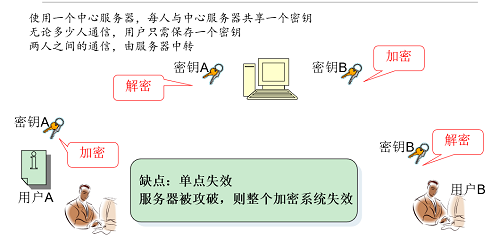
- 密钥管理中心(KMC)方案
- 密钥分散方案
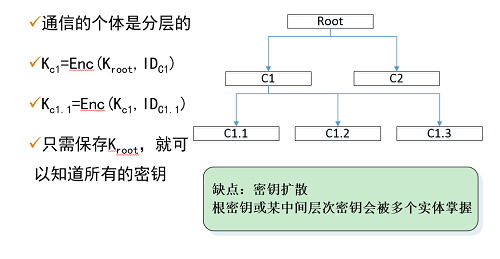
- 使用公钥技术进行密钥管理
可以保证：加密传递的数据只能被指定的接收者解密；单个实体的失效不能影响其它实体的安全；密钥不能扩散；密钥易于传递
对称密钥加密方案分类
- 分组密码：分组进行加密，需要满足混淆(密钥与密文之间的关系尽可能复杂)和扩散原则(使明文中的冗余度能扩散到整个密文)。
- 流密码：可看做分组长度为1的分组密码。
- 优点：在传输错误率很高的环境中，具有较大优势，因为流密码中没有错误扩散。也可用于数据处理必须每次一个符号的场景，如设备没有存储区或缓冲区有限。此外，相比分组密码，流密码的硬件实现电路更简单。
- 缺点：低扩散、插入和修改的不敏感性。
- 一次一密(One time pad) 是唯一被证明安全的的系统。
对称密钥加密优点
- 数据高吞吐量，便于软硬件实现。一些硬件实现达到了每秒加密几百兆字节，软件实现的吞吐量也达到了兆字节每秒的量级。
- 密钥相对较短。
- 可作为要素构造各种密码机制。如：伪随机数生成器，杂凑函数，快速数字签名方案。
- 可合成强密码。简单变换容易被分析，但研究其弱点后，可用来构造乘积密码。
- 历史较久远。
对称密钥加密缺点
- 通信双方的密钥均需要保密。
- 大型网络中需要管理许多密钥对。其结果是，有效的密钥管理者需要有一个无条件可信的TTP(在所有事情上都是可信的，它可以访问用户的私钥，还承担着公钥与标识符的联系)，该TTP需要实时使用。
- 密钥需要时常更换，甚至每次会话都需要更换。
- 源自对称密钥加密的数字签名机制通常需要关于公开验证函数的大密钥，或通信协议。
公钥密码学
采用公钥加密的双方通信可用下图表示，公钥密码假设无法通过公钥e得到私钥d的信息。没有一个独立于某种预定的假设的公钥方案被证明是安全的。
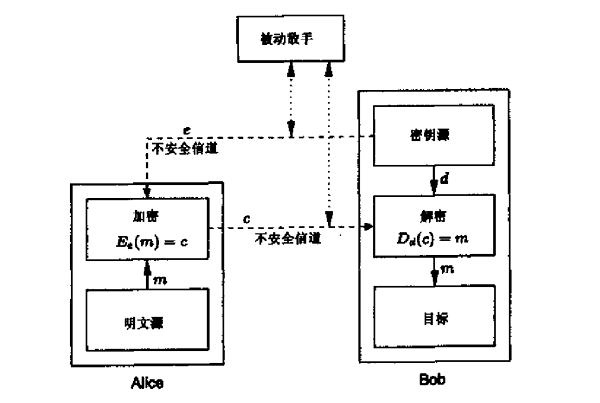
公钥系统中认证的必要性
在公钥系统中，需要对公钥本身的数据源进行认证，否则容易发生如下的假冒攻击。
常见公钥密码算法
-
RSA：基于RSA困难的假定，而非分解大整数的困难假定(因为并不清楚大整数分解是否是破解RSA的唯一方法)；但是若可以分解大整数，则可破解RSA。NIST建议2014年以后，使用2048位以上的大整数。
-
Diffie-Hellman密钥交换协议：一种在通信双方之间协商会话密钥的协议
-
国产SM2公钥密码算法的加密方案：利用公钥产生任意长密钥流，用密钥流与明文模二加获得密文，这实质上就是序列算法。在速度上与对称算法没有实质性差别了。
公钥系统的应用
- 公钥直接加密(速度太慢，不实用)。
- 密码信封方式加密：使用公钥加密对称密码的密钥，使用对称算法加密数据，将两者一起传送给接收方。
- 基于可交换公钥加密的数字签名(需要一种加密算法作为来源)。但是在一些情况下，不允许加密的存在，此时这些数字签名方案就不适用了。
\(D_d(E_e(m)) = E_e(D_d(m)) = m\)
实际应用中，签名用于验证身份，保证不可抵赖性。
公钥加密优点
- 只有私钥需要保密。
- 与无条件可信的TTP相反，公钥密钥管理者只需要一个功能上可信的TTP(它是诚实且公正的，但是无法访问用户私钥)，并且该TTP可以离线使用。
- 一对公钥/私钥可以多次使用甚至多年不变。
- 许多公钥方案产生了相对有效的数字签名机制，用于刻画公开验证函数的密钥通常比对称密钥小得多。
- 在大型网络中，所需密钥的数量要比对称密钥少很多。
公钥加密缺点
- 吞吐量上，大多流行的公钥方案要比已知最好的对称密钥方案慢几个数量级。
- 密钥长度比对称密钥大很多(如RSA的1024比特对比对称密码的64或128比特)；公钥签名的大小也比对称密钥技术提供的数据源认证标记(MAC)大很多。
- 还没有公钥方案被证明是安全的(对分组密码也可以这么说)。至今发现的有效公钥加密方案都基于数学困难问题。
- 历史较短，始于1977年RSA的提出。
两者比较
对称和公钥有许多互补的优点。目前的密码系统融合了两者的优势。例如：
- 凭借公钥加密技术建立密钥(密钥可长期使用)
- 将该密钥作为对称密钥进行双方通信(高吞吐量)
在实际应用中，
- 公钥密码学推动了有效的签名(特别是不可抵赖性)和密钥管理。
- 对称密码学对于加密及数据完整性应用很有效。
