Python pandas库和stats库计算偏度和峰度(附程序)

pandas库

• 样本方差无偏估计：
  \(\frac{1}{n-1}\sum_{i=1}^{n}\left(x_i-\bar{x}\right)^2\)

• 偏度无偏估计：
  \(g_1=\frac{k_3}{k_2^{\frac{3}{2}}}=\frac{n^2}{\left(n-1\right)\left(n-2\right)}\frac{m_3}{s^3}=\frac{n^2}{\left(n-1\right)\left(n-2\right)}\frac{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^3}}{{\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\overline{x})^2}}}^3}=\frac{\sqrt{n\left(n-1\right)}}{\left(n-2\right)}\frac{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^3}}{{\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2}}}^3}\)

• 峰度无偏估计：
  

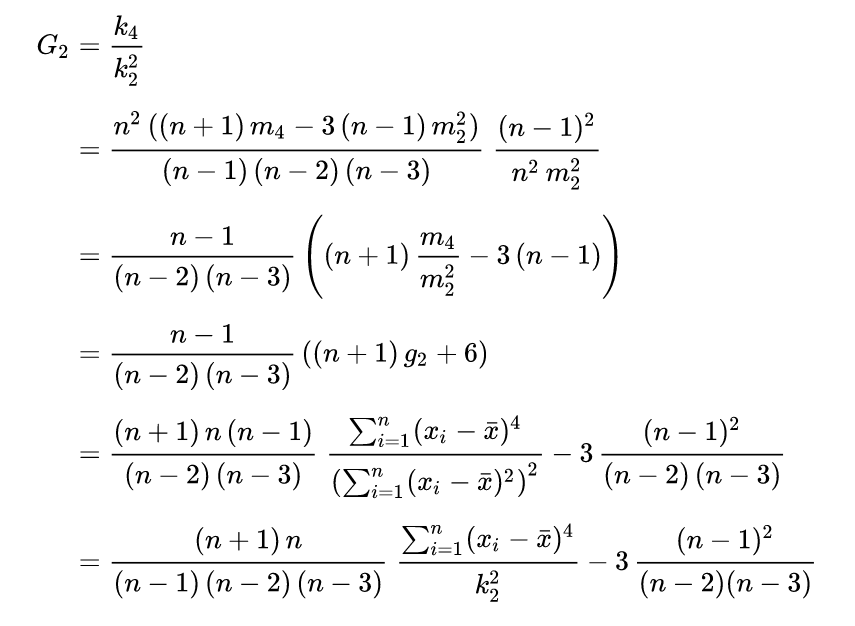
stats库

• 偏度有偏估计：
  \(b_1=\frac{m_3}{s^3}=\frac{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^3}}{{\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2}}}^3}\)

• 峰度有偏估计：
  \(g_2=\frac{m_4}{m_2^2}-3=\frac{\frac{1}{n}\sum_{i-1}^{n}{(x_i-\overline{x})^4}}{(\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2})^2}-3\)

原始定义

• 偏度
  \(b_1=\frac{m_3}{s^3}=\frac{\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^3}}{{\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\overline{x})^2}}}^3}\)

• 峰度
  \(g_2=\frac{m_4}{m_2^2}-3=\frac{\frac{1}{n}\sum_{i-1}^{n}{(x_i-\overline{x})^4}}{(\frac{1}{n}\sum_{i=1}^{n}{(x_i-\overline{x})^2})^2}-3\)

#!/usr/bin/python
# -*- coding: UTF-8 -*-

import pandas as pd # pandas是科学计算的库，主要用于数据分析
import numpy as np # 导包
from scipy import stats # scipy是开源数值计算，科学与工程应用的开源库 (scipy.stats)主要用于统计
#偏度与峰度

x=[53, 61, 49, 66, 78, 47] # 列表[1,6]
n = len(x) # n为x中数据个数

######## 使用pandas计算偏度与峰度
s=pd.Series(x)#将列表x转换为pandas中的Series，其实就相当于一维的矩阵
print('***************使用pandas计算的偏度与峰度(无偏)***************')
print('偏度  = ',s.skew(),'峰度:',s.kurt()) # 计算偏度和峰度
print()

######## 使用stats计算偏度与峰度
print('***************使用stats计算的偏度与峰度(有偏)***************')
skew=stats.skew(x)#使用stats计算偏度
kurtosis = stats.kurtosis(x)#使用stats计算峰度
print('偏度 =',skew,'峰度 =',kurtosis)
print()

######## 使用文本中公式计算的偏度与峰度
print('***************使用文本中公式计算的偏度与峰度***************')
R_mean = np.mean(x) # 均值 
R_var = np.var(x,ddof = 1)  # 方差(除以n-1)
R_var1 = np.var(x) # 方差(除以n)
R_sc = np.mean((x - R_mean)** 3)/(R_var**3)**.5 #偏度使用除以n-1的方差
R_ku = np.mean((x - R_mean)**4)/R_var1**2-3 #峰度使用除以n的方差
print('偏度 =',R_sc,'峰度 =',R_ku)

###### 此部分可用于验证pandas的计算结果 ###### 
# R_sc = 30**0.5*np.mean((x - R_mean)**3)/(R_var1**3)**.5 /4# 偏度
# R_ku = (n+1)*n/(n-1)/(n-2)/(n-3)*sum((x - R_mean)**4)/(R_var**2)-3*(n-1)*(n-1)/(n-2)/(n-3) # 峰度
# print([R_sc, R_ku])#输出偏度、峰度


###################################################################
######################设置参数计算有偏和无偏#########################
###################################################################
print()
print('###################################################################')
print('######################设置参数计算有偏和无偏#########################')
print('###################################################################')

def skewAndkurt(x,parm):
    '''
    parm = 2: 使用文本中公式计算的偏度与峰度(有偏)
    parm = 1: 使用pandas计算的偏度与峰度(无偏)
    parm = 0: 使用stats计算的偏度与峰度(有偏)
    '''
    if parm == 2:
        print('parm = 2 , 使用文本中公式计算的偏度与峰度(有偏):')
        R_mean = np.mean(x) # 均值 
        R_var = np.var(x,ddof = 1)  # 方差(除以n-1)
        R_var1 = np.var(x) # 方差(除以n)
        R_sc = np.mean((x - R_mean)** 3)/(R_var**3)**.5 #偏度使用除以n-1的方差
        R_ku = np.mean((x - R_mean)**4)/R_var1**2-3 #峰度使用除以n的方差
        print('偏度 =',R_sc,'峰度 =',R_ku)
    if parm == 1:
        print('parm = 1 , 使用pandas计算的偏度与峰度(无偏):')
        s=pd.Series(x) # 使用pandas计算的偏度与峰度(无偏)
        print('偏度  = ',s.skew(),'峰度:',s.kurt()) # 计算偏度和峰度
    elif parm == 0: # 使用stats计算的偏度与峰度(有偏)
        print('parm = 0 , 使用stats计算的偏度与峰度(有偏):')
        skew=stats.skew(x) # 使用stats计算偏度
        kurtosis = stats.kurtosis(x)#使用stats计算峰度
        print('偏度 =',skew,'峰度 =',kurtosis)

parm = 0
skewAndkurt(x,0) 
print()   
parm = 1
skewAndkurt(x,1)  
print()   
parm = 2
skewAndkurt(x,2)