LeetCode 1168. Optimize Water Distribution in a Village

题目描述：

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i], or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[i] = [house1, house2, cost] represents the cost to connect house1 and house2 together using a pipe. Connections are bidirectional.

Find the minimum total cost to supply water to all houses.

 

Example 1:

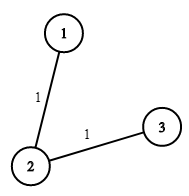
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: 
The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3. 

Constraints:

• 1 <= n <= 10000
• wells.length == n
• 0 <= wells[i] <= 10^5
• 1 <= pipes.length <= 10000
• 1 <= pipes[i][0], pipes[i][1] <= n
• 0 <= pipes[i][2] <= 10^5
• pipes[i][0] != pipes[i][1]

题解：

1、wells数组可以看成是从村庄0到index处之间连接的代价

2、村庄（编号为1～n）有水只需要该村庄有通到村庄0的通路即可-即只需要把所有村庄连通即可，即形成一棵最小生成树，可采用Kruskal算法：即：

按照边的权重顺序（从小到大）将边加入生成树中，但是若加入该边会与生成树形成环则不加入该边。直到树中含有{\displaystyle V-1}条边为止。这些边组成的就是该图的最小生成树。

Kruskal算法的时间复杂度为{\displaystyle E\log E}。

3、判断两个村庄是否相连可采用并查集。Lee215的实现如下：

int[] uf;
    public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
        uf = new int[n + 1];
        List<int[]> edges = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            uf[i + 1] = i + 1;
            edges.add(new int[] {0, i + 1, wells[i]});
        }
        for (int[] p : pipes) {
            edges.add(p);
        }
        Collections.sort(edges, (a, b) -> Integer.compare(a[2], b[2]));

        int res = 0;
        for (int[] e : edges) {
            int x = find(e[0]), y = find(e[1]);
            if (x != y) {
                res += e[2];
                uf[x] = y;
                --n;
            }
        }
        return res;
    }

    private int find(int x) {
        if (x != uf[x]) uf[x] = find(uf[x]);
        return uf[x];
    }

这种实现十分简洁。

我的实现套用了自己常用的一套模版的类WQUPC（weighted quick union with path comparess），显得有些冗余，不过能够提升性能。

class Solution {
    class WQUPC {
        int[] id;
        int[] sz;
        WQUPC(int n) {
            id = new int[n];
            sz = new int[n];
            for(int i = 0; i < n; i++) {
                id[i] = i;
                sz[i] = 1;
            }
        }
        int root(int i) {
            while(id[i] != i) {
                id[i] = id[id[i]];
                i = id[i];
            }
            return id[i];
        }
        boolean connected(int i, int j) {
            return root(i) == root(j);
        }
        boolean union(int i, int j) {
            int pi = root(i);
            int pj = root(j);
            if(pi == pj) return false;
            if(sz[pi] > sz[pj]) {
                id[pj] = id[pi];
                sz[pi] += sz[pj];
            } else {
                id[pi] = id[pj];
                sz[pj] += sz[pi];
            }
            return true;
        }
    }
    
    public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
        List<int[]> edges = new ArrayList<>();
        for(int i = 0; i < wells.length; i++) {
            edges.add(new int[]{0, i + 1, wells[i]});
        }
        for(int[] pipe : pipes) {
            edges.add(new int[]{pipe[0], pipe[1], pipe[2]});
        }
        Collections.sort(edges, (a, b) -> Integer.compare(a[2], b[2]));
        WQUPC qu = new WQUPC(n + 1);
        int res = 0;
        for(int[] edge : edges) {
            if(qu.union(edge[0], edge[1])) {
                // System.out.println(edge[0] + " " + edge[1] + " " + edge[2]);
                res += edge[2];
            }
        }
        return res;
    }
}