点击率模型AUC
一 背景
首先举个例子:
正样本(90) 负样本(10)
模型1预测 正(90) 正(10)
模型2预测 正(70)负(20) 正(5)负(5)
结论:
模型1准确率90%;
模型2 准确率75%
考虑对正负样本对预测能力,显然模型2要比模型1好,但对于这种正负样本分布不平衡对数据,准确率不能衡量分类器对好坏了,所以需要指标auc解决倾斜样本的评价问题。
二分类混淆矩阵
预测\实际 1 0
1 TP FP
0 FN TN
TPR=TP/P=TP/TP+FN 直观1中猜对多少
FPR=FP/N=FP/FP+TN 直观0中猜错多少
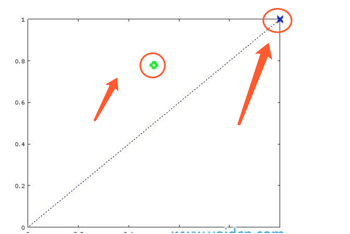
Auc对横纵坐标分别为FPR和TPR,相对于y=x这条直线靠近左上角对分类器性能更好,所以模型2更优。
TPR FPR
模型1 90/90=1 10/10=1
模型2 70/90=0.78 5/10=0.5
模型1和2的auc点位分别如下图所示,显然模型1更优:
二 研究现状
AUC直观概念,任意取一对正负样本,正样本score大于负样本对概率。
计算方法:正样本和负样本pair对,auc=预估正样本score大于负样本score的pair对数/总的pair对数。
E.g. 分别计算模型1和2对auc?
四个样本label为y1=+1, y2=+1, y3=-1, y4=-1
模型1的预测为 y1=0.9, y2=0.5, y3=0.2, y4=0.6
模型2的预测为 y1=0.1, y2=0.9, y3=0.8, y4=0.2
解:
模型1: 正样本score大于负样本的pair包括(y1, y3), (y1, y4), (y2, y3),auc为3/4=0.75
模型2: 正样本score大于负样本的pair包括(y2, y3),(y2, y4),auc为2/4=0.5
计算参考paper:《 An introduction to ROC analysis 》(Tom Fawcett)
方法:
1按照score对样本排序;
2依次对每个样本,label分对TP增1,否则FP增1。计算每个小梯形的面积。
3累加所有样本,计算auc
代码:
import sys def scoreAUC(labels,probs): i_sorted = sorted(range(len(probs)),key=lambda i: probs[i], reverse=True) auc_temp = 0.0 TP = 0.0 TP_pre = 0.0 FP = 0.0 FP_pre = 0.0 P = 0; N = 0; last_prob = probs[i_sorted[0]] + 1.0 for i in range(len(probs)): if last_prob != probs[i_sorted[i]]: auc_temp += (TP+TP_pre) * (FP-FP_pre) / 2.0 TP_pre = TP FP_pre = FP last_prob = probs[i_sorted[i]] if labels[i_sorted[i]] == 1: TP = TP + 1 else: FP = FP + 1 auc_temp += (TP+TP_pre) * (FP-FP_pre) / 2.0 auc = auc_temp / (TP * FP) return auc def read_file(f_name): f = open(f_name) labels = [] probs = [] for line in f: line = line.strip('\n').split(',') try: label = int(line[0]) prob = float(line[1]) except ValueError: # skip over header continue labels.append(label) probs.append(prob) return (labels, probs) def main(): if len(sys.argv) != 2: print("Usage: python scoreKDD.py file") sys.exit(2) labels, probs = read_file(sys.argv[1]) auc = scoreAUC(labels, probs) print("%f" % auc) if __name__=="__main__": main()
三 点击率模型auc计算方法
如上图,以两个分桶为例,每个分桶计算的AUC为图中的阴影部分。全局AUC部分需要补充P3部分的面积,等于前i-1个桶的sum(click)乘以每i个桶的noclick。
整体的AUC就是曲线下的面积除以曲线的起点、终点锚定矩型的面积。
步骤
1按照pctr聚合 sum_show和sum_clk;
2样本按照pctr排序;
3依次对每个样本,计算noclk和clk围成对小梯形对面积。
代码:
import sys #init auc dict params_auc_dict = {"last_ctr":1.1, "slot_show_sum":0, "slot_click_sum":0, \ "auc_temp":0.0, "click_sum":0.0, "old_click_sum":0.0, "no_click":0.0, \ "no_click_sum":0.0} #init q distribute q_bucket = 1000 params_Q_dict = {"count_list":[0]*(q_bucket+1)} for line in sys.stdin: lineL = line.strip().split('\t') if len(lineL) < 3: continue pctr = float(lineL[0]) #print lineL[0] #pctr = float(lineL[0])/1e6 show = int(float(lineL[1])) click = int(float(lineL[2])) slot_info = '-' ### calculate auc params_auc_dict["slot_show_sum"] += show params_auc_dict["slot_click_sum"] += click if params_auc_dict["last_ctr"] != pctr: params_auc_dict["auc_temp"] += (params_auc_dict["click_sum"] + \ params_auc_dict["old_click_sum"]) * params_auc_dict["no_click"] / 2.0 params_auc_dict["old_click_sum"] = params_auc_dict["click_sum"] params_auc_dict["no_click"] = 0.0 params_auc_dict["last_ctr"] = pctr params_auc_dict["no_click"] += show - click params_auc_dict["no_click_sum"] += show - click params_auc_dict["click_sum"] += click ### calculate Q distribution index = int(pctr / (1.0/q_bucket)) #interval [0, 0.001) left close, right open count_list = params_Q_dict["count_list"] count_list[index] += show # last instance for auc params_auc_dict["auc_temp"] += (params_auc_dict["click_sum"] + \ params_auc_dict["old_click_sum"]) * params_auc_dict["no_click"] / 2.0 if params_auc_dict["auc_temp"] > 0: auc = params_auc_dict["auc_temp"] / (params_auc_dict["click_sum"] * params_auc_dict["no_click_sum"]) else: auc = 0 print "AUC:%s\tshow_sum:%s\tclk_sum:%s" %( auc, params_auc_dict["slot_show_sum"], params_auc_dict["slot_click_sum"]) #print Q distribution result for item in params_Q_dict: count_list = params_Q_dict["count_list"] print "Max bucket num: %s" %(sum(count_list)) for i in range(q_bucket+1): if i < (q_bucket - 1): print str((i+1)*(1.0/q_bucket)) + '\t' + str(count_list[i]) else: print '1.0\t' + str(count_list[i]+count_list[i+1]) break



