神经网络-Backpropagation算法
目录
1.背景
1.1大话神经网络结构
神经网络模型以人脑中的圣经网络受启发,有多个版本。最著名的的算法是1980年的backpropagation。

图1
神经网络的结构分为3部分,如图1所示,输入层和输出层只有一层,中间隐藏层有很多。其中,输入层是由训练集的实例特征向量传入的,经过连接结点的权重传入下一层,一层的输出是下一层的输入。隐藏层的个数可以是任意的,没有明确的规则来设计需要多少个隐藏层。理论上来说,只要数据足够大且隐藏层足够的多,那么理论上来说神经网络可以模拟出任何的方程。
1.2 模型的确定
模型的确定分为两个部分,即确定层数和每层的单元数。
确定模型的时候需要注意如下细节:
- 特征向量在被传入输入层时通常先被标准化到0与1之间(为了加速学习过程)。
- 离散型变量在被传入前要先转化成哑变量。
-
神经网络可以做分类问题,也可以解决回归问题。
如果是2类,用一个输出单元表示。
如果是多个类,每一个类用一个输出单元表示。
比如:有6个类{0,1,2,3,4,5},则设置6个输出单元。
1.3 模型的检验
检验模型的好坏的一个指标就是模型的精度,那么如何检验模型的精度呢?
毫无疑问,首选交叉验证法,这在机器学习里也是老套路了。具体做法见图2。
交叉验证法
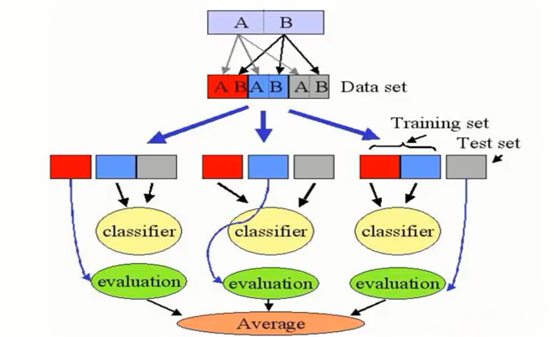
图2
2.算法详解—Backpropagation
2.1 算法思路
正向实验
数据1àbias和weight更新
数据2àbias和weight更新
…
数据nàbias和weight更新
最终每条线上的weight和bias
反向优化
根据损失函数最小的原则,来优化模型的参数。
2.2 伪操作
2.2.1 正向实验
Step1:
输入:数据集D,学习率,一个多层向前神经网络
输出:一个训练好的神经网络
Step2:初始化权重weight和偏向bias:随机初始化在(-1,1)之间,或者在(-0.5,0.5)之间。计算(见图3和式(1))并加上一个偏向Bias,最后将结果非线性处理(见图4和式(2))。
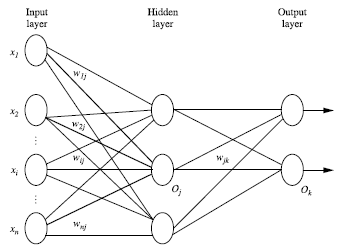
图3
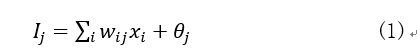
所谓非线性处理就是讲结果
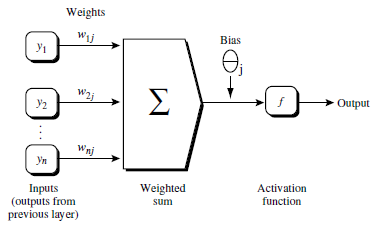
图4
Activation function:

2.2.2 反向优化
对于输出层

对于隐藏层
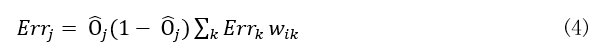
式(4)的本质:输出层的节点j的误差和节点i与节点j之间的权重来作为权重,来计算中间层节点i的误差。
利用梯度下降算法计算最小误差
权重更新
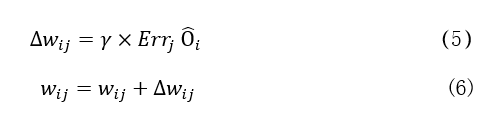
偏向更新

3. 终止条件
3.1 学习率角度
快找到最小值了,权重的更新低于某个阈值
3.2 错误率角度
预测的错误率小于某个阈值
3.3 迭代次数
达到预设的某个迭代次数
4. 实例
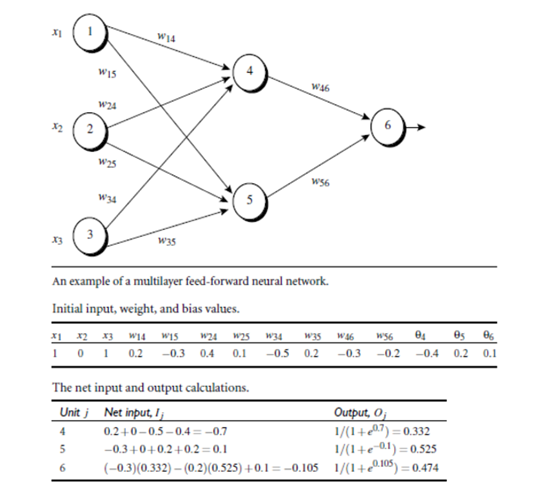

Hinton加深了神经网络的深度,(使中间层更加的复杂)从此神经网络超过SVM等,突破了所有的传统算法。这就是Deep Learning的原型Backpropagation算法。


