机器学习第二次作业
第一章节
导图
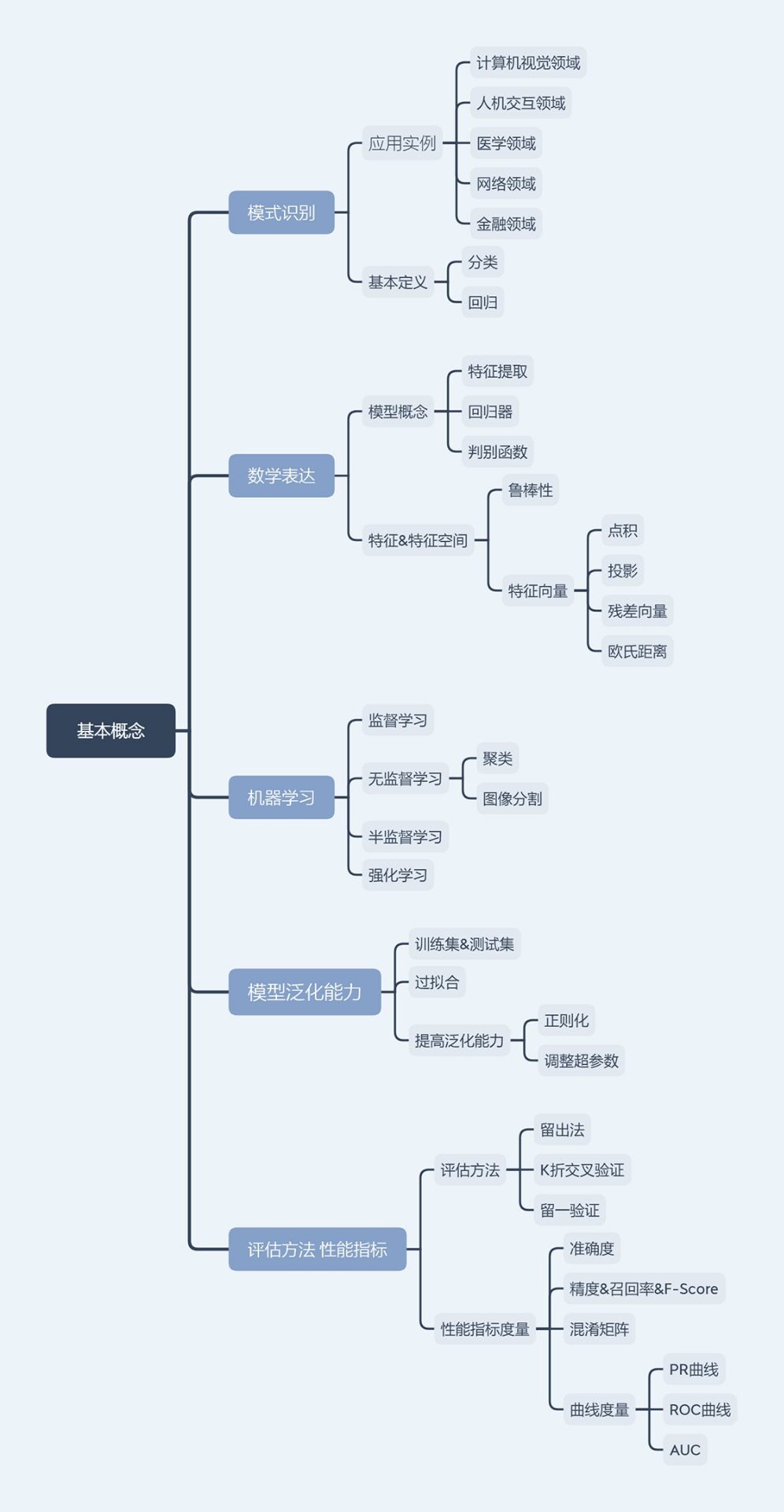
知识点总结归纳
-
第一节
-
模式识别的应用实例
-
分类与回归
分类：输出量是离散的表达 （二类/多类分类）
回归：输出量是连续的信号表达 （单个/多个维度）
-
-
第二节
-
模型
用于回归 特征提取：从原始输入获取有效信息
回归器：将特征值映射到回归值
用于分类 分类器：回归器+判别函数
判别函数：sign函数(二分类) max函数(多类分类)
-
特征&特征空间
鲁棒性：针对不同的观测调节，仍能有效表达类别之间的差异性
特征向量：多个特征构成列向量
-
-
第三节
-
特征向量相关性
特征向量点积：
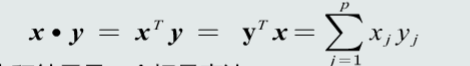
点积结果是一个标量表达，点积具有对称性，是一个线性变换，
几何意义：点积可以表示方向上的相似度，为0说明两个向量是正交的
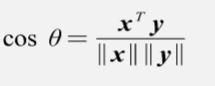夹角说明两个向量在方向上的差异性特征向量投影：
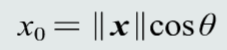将向量x垂直投影到向量y方向上的长度 含义：向量x分解到向量y方向上的程度，分解的越多，两个向量方向越相似
点积可以通过投影表达：向量x y的点积=向量x→y的投影×向量y的模长
如果向量y是一个单位向量，则向量x y之间的点积等于向量x到向量y的投影
残差向量：向量x分解到向量y方向上得到的投影向量与原向量x的误差
欧氏距离：两个向量间的相似程度
-
-
第四节
-
模型得到
线性模型：
适用于数据是线性可分/线性表达的数据
非线性模型：（曲面，曲线，超曲面）适用于线性不可分/线性不可表达的数据
目标函数：代价函数 损失函数
-
机器学习方式
监督式学习：训练样本以及输出真值都给定情况下机器学习算法
无监督式学习：只给定训练样本，没有给输出真值的机器学习算法
半监督学习：既有标注的训练样本，又有未标注的训练样本情况下的学习算法
强化学习：机器自行探索决策，真值滞后反馈的过程
-
-
第五节
-
模型泛化能力
训练集：模型训练所用的样本数据
测试集：测试模型所用的样本数据
泛化能力：训练得到的模型不仅要对训练样本具有决策能力，还要对新的模式具有决策能力
过拟合：模型训练阶段表现很好，测试阶段表现很差，模型过于拟合训练数据
防止过拟合：模型选择合适的多项式阶数
正则化，调节正则系数降低过拟合程度
-
-
第六节
-
评估方法
留出法：将数据集随机分为两组 训练集和测试集
K折交叉验证：
留一验证：每次只取数据集中的一个样本做测试集，剩余的做训练集
-
性能指标度量
准确度：将阳性阴性综合起来度量识别正确的程度
精度：预测为阳性样本的准确程度
召回率：敏感度，全部阳性样本为阳性比例
F-Score：加权平均，综合精度和召回率
混淆矩阵：矩阵的列表示预测值，行表示真值 对角线元素值越大模型性能越好
曲线度量：PR曲线 横轴召回率 纵轴精度
ROC曲线 横轴度量所有阴性样本被识别为阳性的比例 纵轴召回率
AUC曲线下方面积 =1完美分类器 <0.5比随机猜测还差 >0.5优于随机猜测
-
课后总结
模式识别是根据已有知识的表达，针对待识别模式，判别决策其所属的类别或者预测其对应回归值。其数学解释可以看作为一种函数映射f(x)，将待识别模式x从输入空间映射到输出空间。
模型防止过拟合，应该提高其泛化能力，选择合适的模型+正则化，模型可用评估方法评价其。
第二章节
导图
知识点总结归纳
-
第一节
-
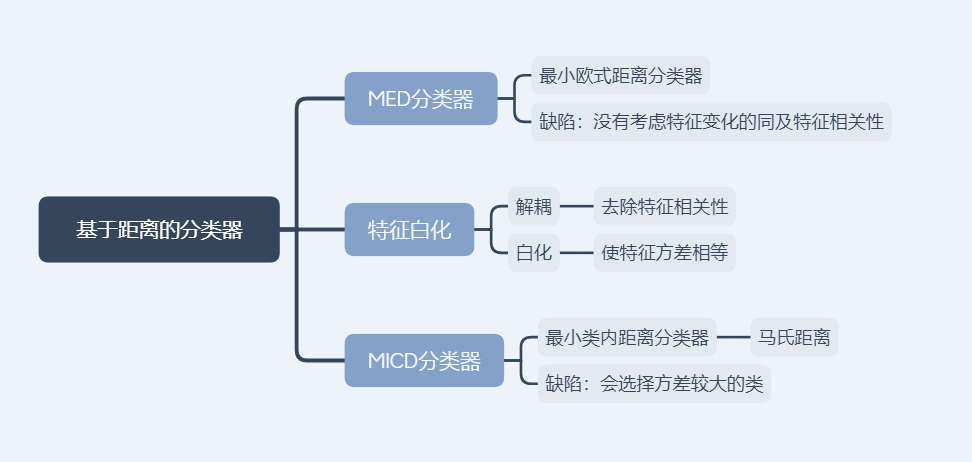
基于距离分类
定义：把测试样本到每个类之间距离作为决策模型，将测试样本判定为其距离最近的
该类所有训练均值作为类的原型
原型种类：
最近邻：从一类的训练样本中，选取与测试样本距离最近的一个训练样本，作为该类的原型，类原型取决于测试样本
距离度量：欧氏距离，曼哈顿距离，加权欧式距离
MED分类器：最小欧式距离，类的原型为均值
-
-
第二节
-
特征白化
目的：将原始特征映射到一个新的特征空间，使得新空间中特征协方差为单位矩阵，从而去除特征变化的不同及特征之间的相关性
特征转化：解耦（去除特征相关性），白化（使每维特征方差相等）
-
-
第三节
-
MICD分类器
最小类内距离分类器，基于马氏距离的分类器
缺陷是选择方差较大的类
-
课后总结
MED分类器采用欧式距离为距离度量，没考虑特征变化的不同及特征之间的相关性，MICD考虑了特征之间的相关性，但是其缺陷会选择方差较大的类。
第三章节
导图
知识点总结归纳
-
第一节
-
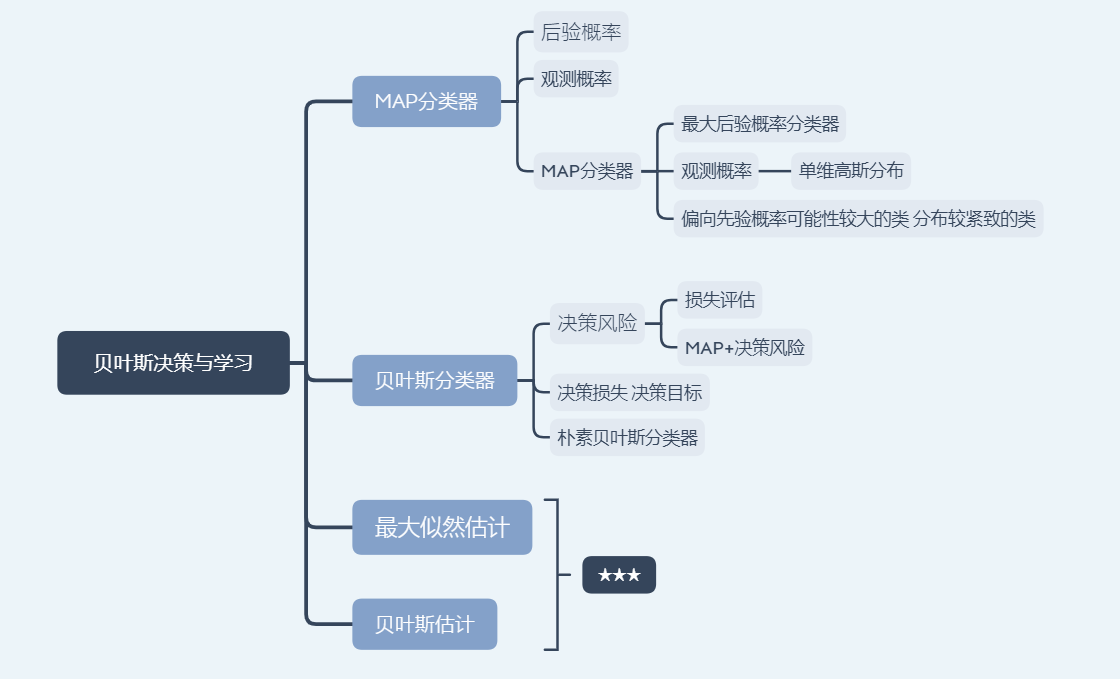
贝叶斯决策与MAP分类器
后验概率：表达给定模式x属于类Ci可能性 P(Ci|x)
贝叶斯规则：
MAP分类器：将测试样本决策分类给后验概率最大的那个类
-
-
第二节
-
MAP分类器
观测概率：单位高斯分布
分类器决策偏向于先验概率高的类，分布较为紧致的类
-
-
第三节
-
决策风险与贝叶斯分类器
贝叶斯决策不能排除错误判断的情况，因此带来决策风险
贝叶斯分类器决策目标：最小化期望损失
朴素贝叶斯分类器，特征维度高，简化
-
-
第四节
-
最大似然估计
监督式学习根据概率分布形式可分为：参数化方法，非参数化方法
参数估计方法：最大似然估计，贝叶斯估计
-
-
第五节
-
最大似然估计偏差
无偏估计：一个参数估计量的数学期望是该参数的真值
高斯分布的均值是无偏估计，协方差是有偏估计
-
-
第六节第七节
-
贝叶斯估计
贝叶斯估计：给定参数θ分布的先验概率以及训练样本，估计参数θ分布的后验概率
贝叶斯估计具有不断学习的能力，最初少量的训练样本，不太准确的估计，随着训练样本增加，串行不断修正参数估计值，从而达到该参数的期望真值
-
-
第八节
-
KNN估计
K近邻：给定x，找到其对应区域R使其包含k个训练样本，以此计算P(X)
优点：可以自适应的确定相关的区域R范围
缺点：KNN概率密度估计不是连续函数，不是真正的概率密度表达
-
-
第九节
-
直方图估计
基于无参数概率密度估计的基本原理
直接把特征空间分为m个格子，每个格子一个区域R，区域位置固定，平分格子大小，区域大小固定，k值不用给定 得到的概率密度不连续
优点：固定区域R减少由于噪声造成估计误差
-
核密度估计
也是基于无参数概率密度估计的基本原理
核函数：高斯分布，均匀分布，三角分布
确定：不提前根据训练样本估计每个格子统计值，所以要存储所有训练样本
-
课后总结
MAP分类器基于贝叶斯分类器引入决策误差，MAP分类器决策目标是分类误差最小化
第四章节
导图
知识点总结归纳
-
第一节
-
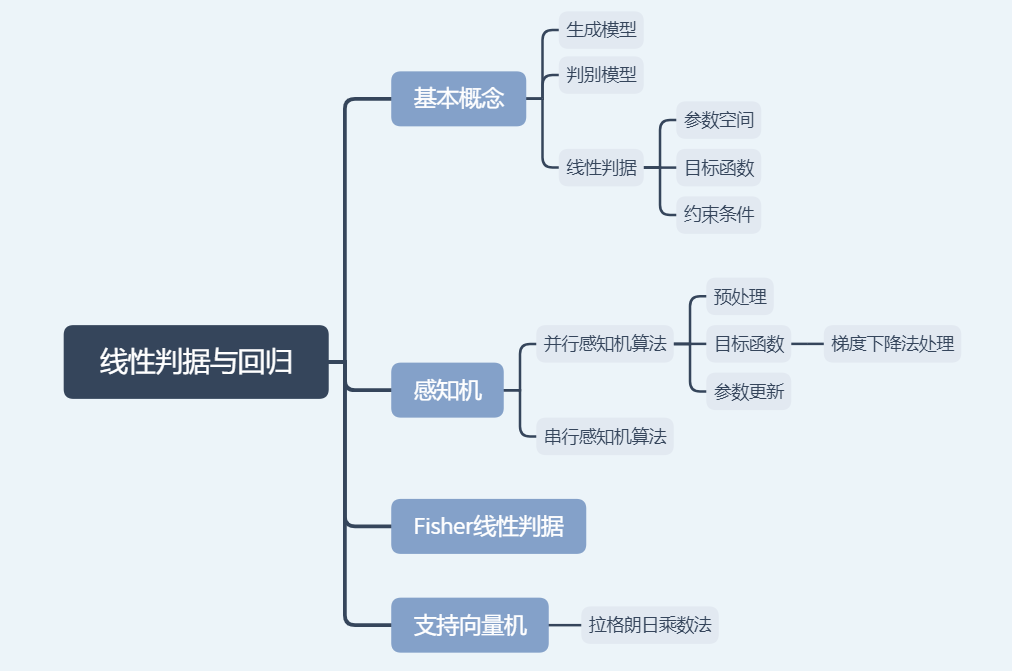
生成模型
给定训练样本{Xn}，直接在输入空间内学习器概率密度函数p(x)
优势：根据p(X)采样新的样本数据，可以检测较低概率的数据，实现离群点检测
劣势：高纬x需要大量训练样本才能准确估计p(x)，否则会出现维度灾难
-
判别模型
给定训练样本{Xn}，直接在输入空间内估计后验概率p(Ci|x)
优势：快速，省去了耗时的高纬度观测似然概率估计
-
线性判据
如果判别函数f(x)是线性函数，则f(x)为线性判据
优势：计算量少，适合训练样本较小情况
-
-
第二节
-
线性判据参数
w权重向量，w0偏置量
-
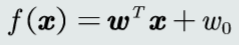
参数空间&解域
参数空间：各个参数维度构成的空间
解域：参数空间中，参数的所有可能解所处范围
-
找最优解
设计目标函数
常见目标函数：误差(均方差),交叉熵。。。
加入约束条件提高泛化能力
-
-
第三节
-
感知机算法
预处理：根据标记过的样本，学习参数w，w0
梯度下降法：使用当前梯度值迭代更新参数
-
串行感知机算法
训练样本是一个个串行给出的
收敛性：感知机算法理论收敛于一个解
步长决定收敛速度，以及是否收敛到全局或者局部最优
-
-
第五节
-
Fisher线性判据
找到一个最合适的投影轴，使两类样本在该轴上投影的重叠部分最少，使得分类效果最佳
投影后，使得不同类别样本分布的类间差异尽量大，同时使得各自类内样本分布离散程度尽量小
-
-
第六节
-
支持向量机
给定训练样本，使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大
-
-
第七节
-
拉格朗日乘数法
最常用对支持向量机的条件优化问题
-
-
第八节
-
主问题
对于不等式约束，主问题难以求解
-
拉格朗日对偶问题
对偶函数自变量为Γ和Λ，与x无关
对偶函数为凹函数，由于木匾函数LD为凹函数，所以对偶问题是凸优化问题
-
-
第九节
-
构建对偶函数
对偶问题的求解是标准的关于λ的二次规划问题
可以调用quadprog函数
-
课后总结
支持向量机目标是最大化总间隔，拉格朗日乘法解决该问题。
